17 de Fevereiro de 2022 30 min de leitura

Índices

Fala, pessoal! Chegamos ao nosso último artigo da série sobre o KNN. Depois de apresentarmos o algoritmo, discutirmos os conceitos de viés e variância e entendermos o que é uma métrica de distância, vamos falar hoje sobre um assunto pouco comentado mas muito importante: a construção de índices. Apresentaremos o que é um índice, o porquê deles serem tão importantes e como construí-los. Mas vamos parar de enrolação e começar logo!

O que é um índice?

Acredito que a maioria de vocês já esteja familiarizada com a ideia de um índice. Seja em livros, sites, listas, etc. um índice é uma ferramenta que nos ajuda a organizar alguma informação. Em livros, por exemplo, os índices são utilizados para indicar quais capítulos existem e em qual página eles estão. “Ok, claro que eu sei o que é um índice. O que isso tem a ver com o KNN? Calma que já chegamos lá!

Por que precisamos de índices?

Antes de entrar diretamente no KNN, vamos usar um exemplo mais simples para entender qual o motivo do uso de índices ser importante. Suponha que você tenha em suas mãos uma lista de nomes. A sua tarefa é encontrar todos os nomes que comecem com a letra “A”. Se a lista estiver ordenada a tarefa é muito simples, não é mesmo? Mas e se ela estiver toda bagunçada? “Sem problema também! É só passar nome a nome”. Essa é uma estratégia muito válida e vamos chamá-la de força-bruta. Quando temos uma lista com 10 nomes, ela parece uma excelente alternativa. Ler 10 nomes não é nada. Mas e se tivéssemos 100 nomes? Complicou um pouco mas ainda é factível. Ok, então. E se tivéssemos 1 milhão de nomes? Nesse cenário, nós ainda poderíamos ler todos os nomes, mas o tempo que vamos levar para fazer isso é muito grande.

E se existisse ferramenta mágica que conseguisse me indicar os lugares exatos em que estão os nomes que começam com as letras entre “A” e “M”. Ia ser incrível, certo? Poder excluir todos os nomes que começam com “N” em diante facilitaria muito o trabalho. E se alguém melhorasse ainda mais a ferramenta e agora ela mostrasse a posição dos nomes iniciados em “A” e “B”? Está parecendo mentira de tão bom, não é? A lista que temos que procurar nomes com “A” agora é muito menor do que a minha lista inicial com 1 milhão de nomes. E pasmem: essa ferramenta mágica existe e é justamente o índice!

O que isso tem a ver com o KNN?

Você já parou para pensar no que aconteceria se tivéssemos que encontrar vizinhos buscando dentre mais de 1 milhão de pontos, por exemplo? Se usássemos a mesma abordagem de “força-bruta”, podemos imaginar que teríamos o mesmo problema de quando uma lista cresce muito: o tempo para a execução do algoritmo ficaria muito maior. Mas será que isso realmente acontece? Vamos dar uma olhada com um pequeno experimento, rodando o KNN para algumas quantidades diferentes de dados.

Código - Tempo KNN

import time
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

n = [1e2, 5e2, 1e3, 5e3, 1e4, 5e4, 1e5, 5e5, 1e6, 5e6, 1e7, 5e7, 1e8]
timer = []
for i in n:
    knn = KNeighborsClassifier(n_neighbors=k, algorithm="brute")
    X, y = make_classification(n_samples=int(i),
                         n_features=2,
                         n_informative=1, 
                         n_redundant=0,
                         flip_y=0.6,
                         random_state=42, 
                         n_clusters_per_class=1,
                         scale=3)
    start = time.perf_counter()
    _ = knn.fit(X,y).predict([[0,0]])
    timer.append(time.perf_counter() - start)

fig, ax = plt.subplots(figsize=(10,6))

ax.plot(n, timer, lw=3, dash_joinstyle="bevel", dash_capstyle="round", c="xkcd:sky blue")
ax.set_xscale("log")
ax.set_xlabel("Número de amostras")
ax.set_ylabel("Tempo (s)")
ax.tick_params(bottom=False, left=False)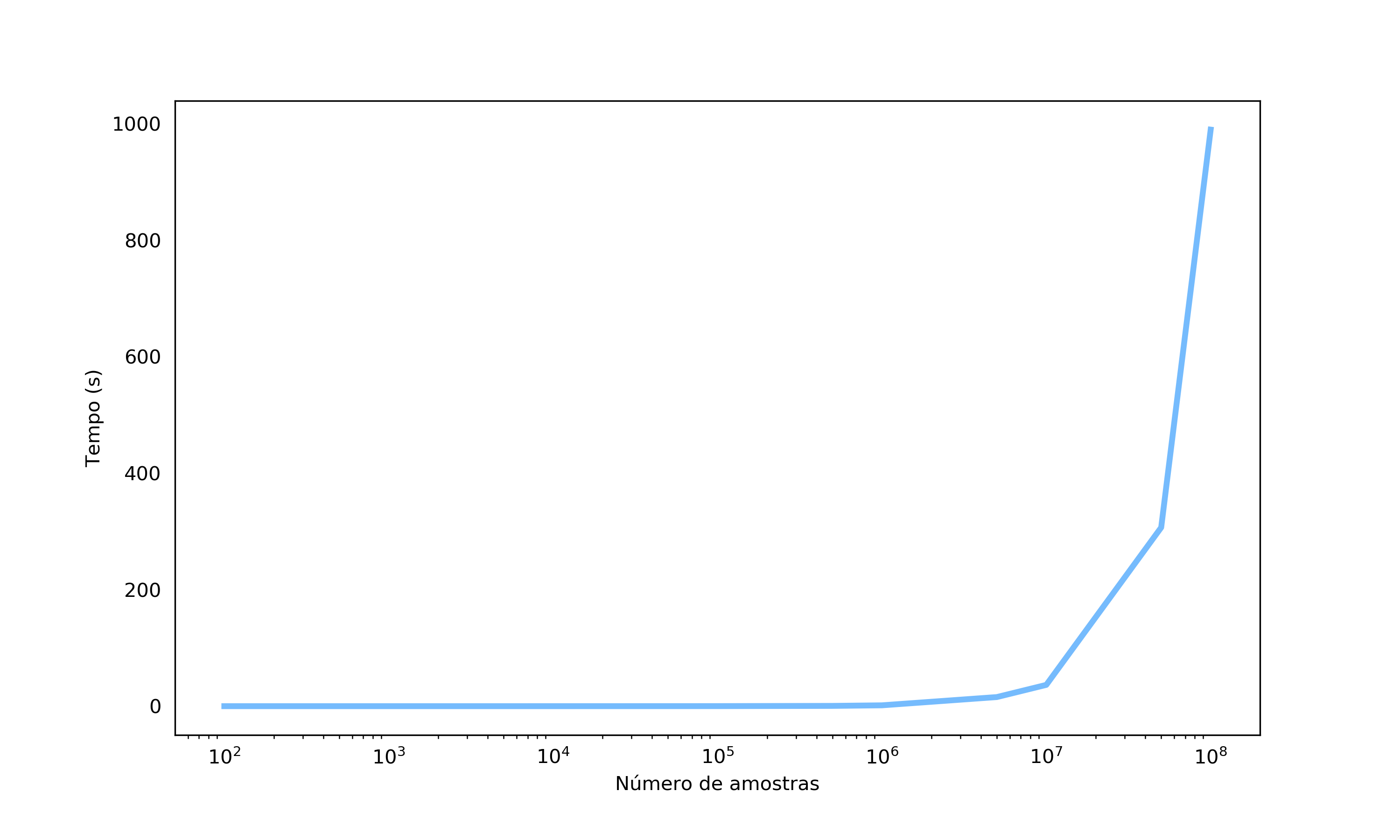

Observando o gráfico, podemos perceber que o tempo de execução do algoritmo cresce exponencialmente com a quantidade de dados. É … realmente parece que temos um problema. Mas nada tema, temos um herói que pode nos auxiliar aqui: os índices! Os índices podem ser fortes aliados para otimização do tempo de busca por vizinhos em algoritmos de distância como o KNN. Especificamente vamos apresentar dois algoritmos para a construção de índices: as KD-Trees e as Ball trees.

KD Tree

As KD-Trees (K Dimensional Trees) ou Árvores K-dimensionais são árvores binárias (ou seja, cada nó tem exatamente 2 filhos) que dividem o espaço original em cortes paralelos aos eixos originais. Que? Cortes paralelos aos eixos? O que raios isso quer dizer? Já chegamos lá e com imagens ficará mais fácil de explicar.

Vamos antes de tudo dar uma olhada no algoritmo de construção do índice:

Para o nó atual, encontre a dimensão (variável) com maior variância;
Faça um corte na mediana dessa dimensão (aqui a ideia é separar 50% dos pontos para cada filho, de forma que a árvore fique balanceada);
O filho da direita conterá os pontos com valor maior do que a mediana naquela dimensão e o filho da esquerda os pontos com valor menor;
Para cada um dos filhos, repita o passo 1.

Muito legal o algoritmo, mas melhor do que isso é um exemplo prático, não é mesmo? Então vamos lá! Para isso vamos utilizar o seguinte conjunto de dados:

Código - Dados

from sklearn.datasets import make_classification

X, y = make_classification(n_samples=100,
                         n_features=2,
                         n_informative=1, 
                         n_redundant=0,
                         flip_y=0.6,
                         random_state=42, 
                         n_clusters_per_class=1,
                         scale=3)

fig, axes = plt.subplots(figsize=(8,6))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()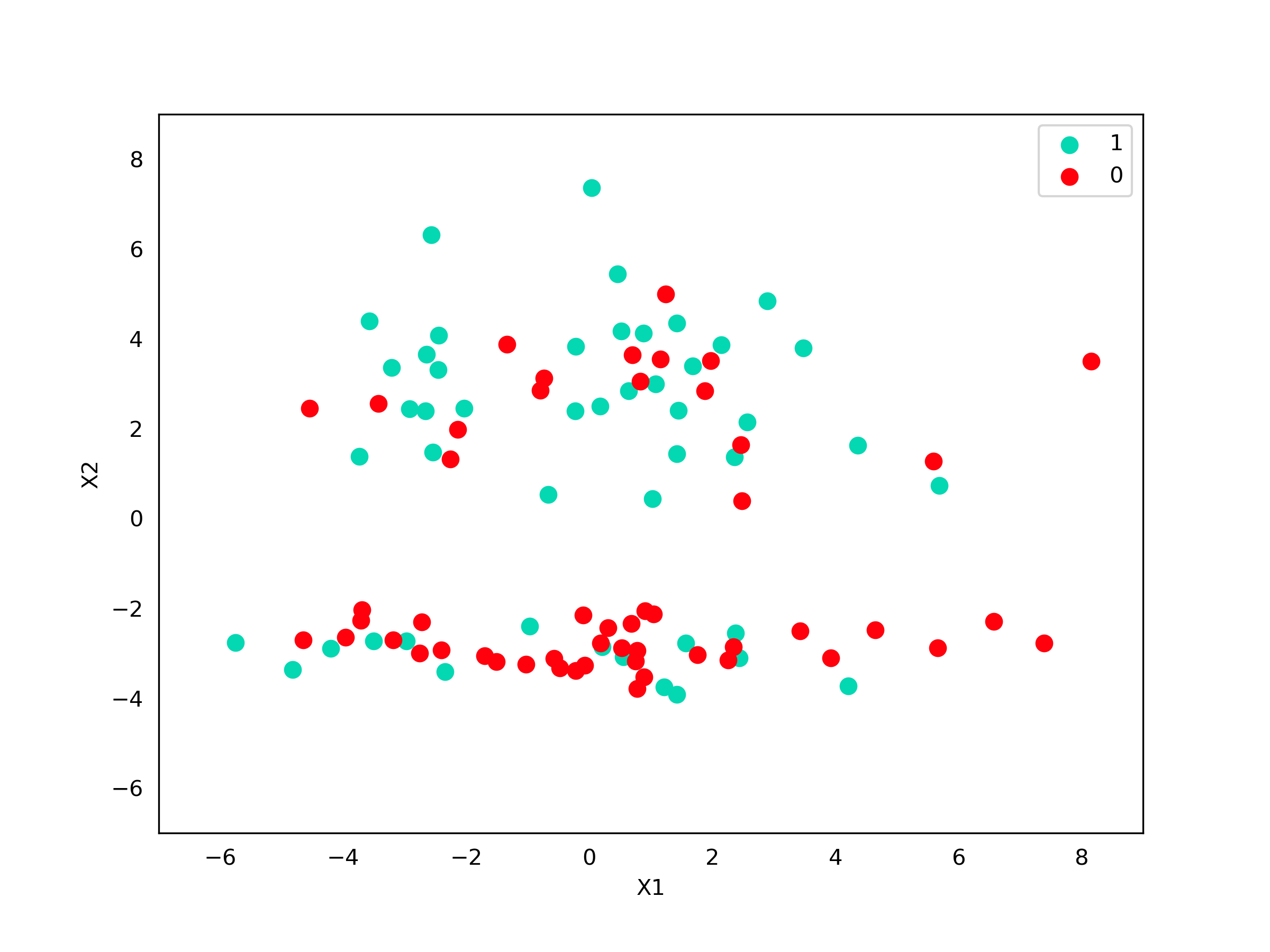

O primeiro passo é calcular a variância em cada dimensão:

Código - Variância

import numpy as np
print(f"Var X1: {X[:, 0].var()}, Mediana X1: {np.median(X[:, 0])}")
print(f"Var X2: {X[:, 1].var()}, Mediana X2: {np.median(X[:, 1])}")

\[\sigma^2(X_1) = 7,93\]

\[\sigma^2(X_2) = 9,73\]

Podemos ver que a variável $X_2$ tem a maior variância e logo ela é a escolhida para realizarmos o corte. Precisamos agora calcular a sua mediana, que é $-0,82$. Vamos observar graficamente como fica nossa divisão.

Código - Imagem

fig, axes = plt.subplots(figsize=(8,6))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()
axes.axhline(-0.82,0,1, lw=3, color="xkcd:light grey", ls="dashed")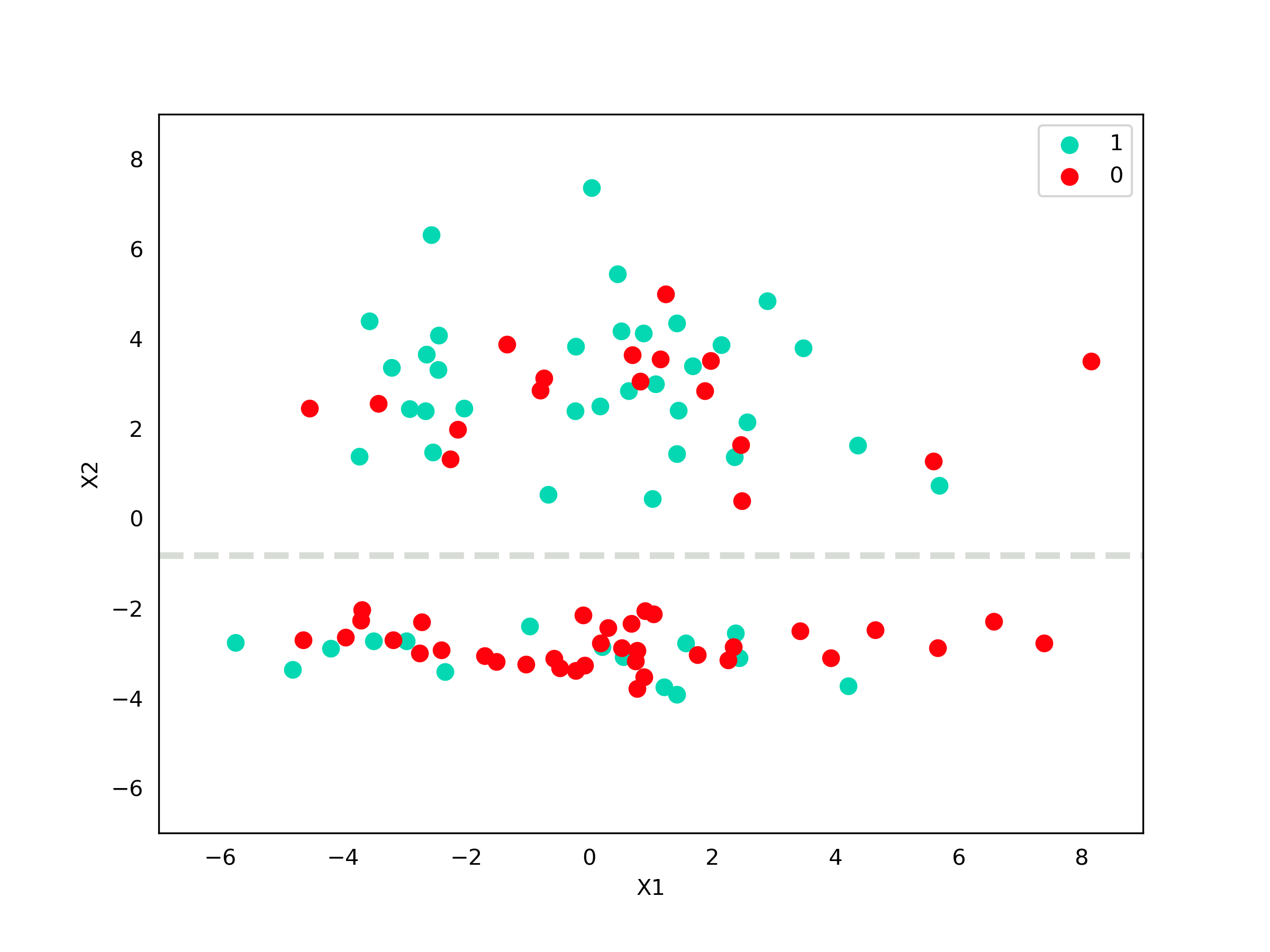

Com essa primeira visualização já podemos entender o que significam os cortes paralelos aos eixos. Perceba que como nossa escolha foi dividir a variável $X_2$, a linha tracejada não toca em momento nenhum o eixo da variável $X_1$. Isso significa que tanto na parte de cima da linha quanto na parte de baixo, $X_1$ pode assumir qualquer valor que ele assumiria antes de realizarmos o corte.

Ótimo! Fizemos nossa primeira divisão e isso já ajuda a reduzir o espaço, mas vamos fazer mais uma iteração só para fixar. Agora temos dois conjuntos de dados: um com os pontos nos quais $X_2$ é maior que -0,82 e outro com os pontos nos quais $X_2$ é menor. Vamos aplicar o mesmo procedimento para cada um desses conjuntos.

Começamos com $X_2 \geq -0,82$, ou seja, a parte superior da linha tracejada. A princípio, a notação abaixo pode parecer meio assustadora, mas ela quer dizer que estamos analisando a variância da variável $X_1$ para todos os pontos na nossa base que tem $X_2 \geq -0,82$ . As demais fórmulas de média e variância seguem o mesmo padrão de notação.

Código - Variância $X_1 \geq -0,82$

print(f"Var X0: {X[X[:,1] >= -0.82, 0].var()}, Mediana X1: {np.median(X[X[:,1] >= -0.82, 0])}")
print(f"Var X1: {X[X[:,1] >= -0.82, 1].var()}, Mediana X2: {np.median(X[X[:,1] >= -0.82, 1])}")

$\sigma^2(X_1|X_2 \geq -0,82) = 7,08$

\[\sigma^2(X_2|X_2 \geq -0,82) = 2,08\]

Dessa forma, agora vamos escolher um novo corte para a parte de cima utilizando a variável $X_1$. A mediana de $X_1$ quando $X_2 \geq -0,82$ é $0,58$.

Código - Imagem

fig, axes = plt.subplots(figsize=(8,6))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()
axes.axhline(-0.82,0,1, lw=3, color="xkcd:light grey", ls="dashed")
axes.axvline(0.58, (-0.82+7)/16, 1,lw=3, color="xkcd:light grey", ls="dashed")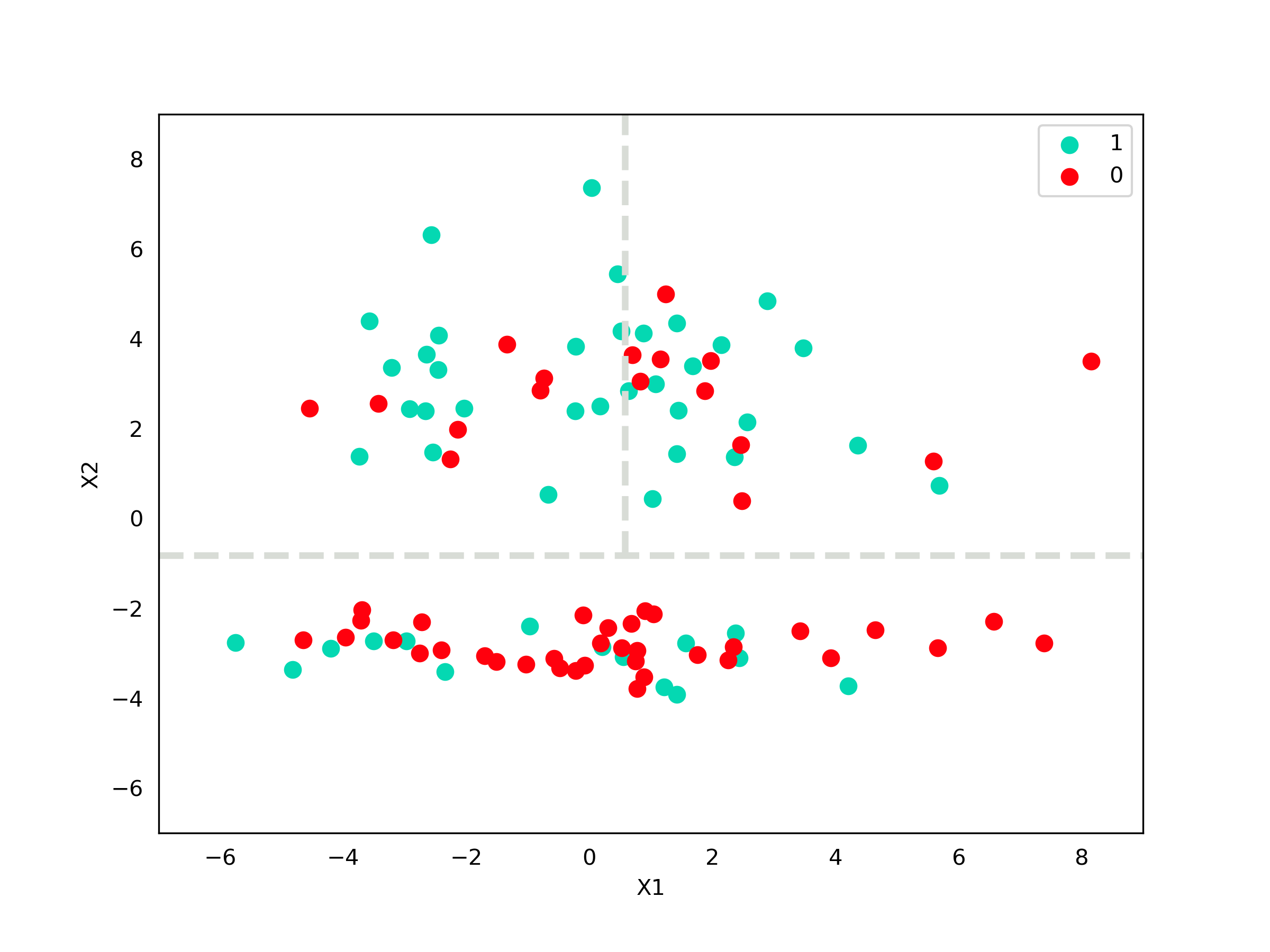

Analogamente para $X_2 \lt -0,82$:

Código - Variância $X_2 \lt -0,82$

print(f"Var X1: {X[X[:,1] < -0.82, 0].var()}, Mediana X1: {np.median(X[X[:,1] < -0.82, 0])}")
print(f"Var X2: {X[X[:,1] < -0.82, 1].var()}, Mediana X2: {np.median(X[X[:,1] < -0.82, 1])}")

\[\sigma^2(X_1|X_2 \lt -0,82) = 8,75\]

\[\sigma^2(X_2|X_2 \lt -0,82) = 0,2\]

Novamente, a dimensão com maior variância é $X_1$ e o valor da mediana é $0,25$.

Código - Imagem

fig, axes = plt.subplots(figsize=(8,6))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()
axes.axhline(-0.82,0,1, lw=3, color="xkcd:light grey", ls="dashed")
axes.axvline(0.58, (-0.82+7)/16, 1,lw=3, color="xkcd:light grey", ls="dashed")
axes.axvline(0.25, 0, (-0.82+7)/16,lw=3, color="xkcd:light grey", ls="dashed")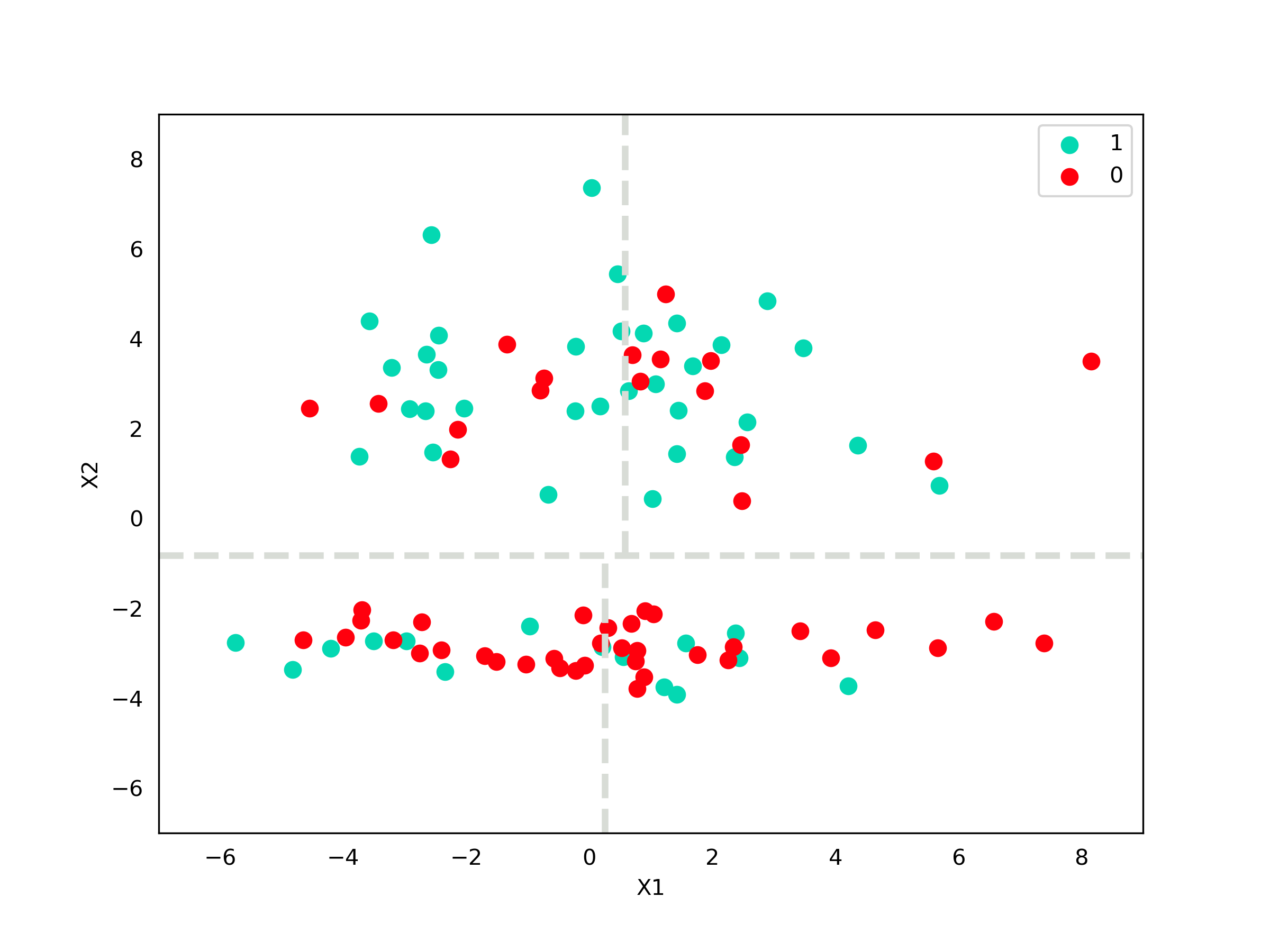

Nós poderíamos continuar dividindo cada espaço ainda, sempre seguindo o mesmo procedimento, mas vamos parar por aqui e discutir como faríamos para procurar os vizinhos. Você se lembra que no nosso exemplo da lista, o índice dizia a posição dos nomes iniciados por “A” e “B”, de modo que só teríamos que procurar nessas posições? A ideia aqui é muito parecida: nós vamos percorrer a árvore, começando pela primeira quebra, para decidir em que região o nosso ponto de interesse se encontra. Dada essa região, podemos buscar os vizinhos apenas dentro dela (ou alguma outra adjacente), restringindo nosso espaço de busca. Mas vamos ao exemplo!

Suponha que queremos procurar vizinhos para o ponto $\text{Z}\ =\ (x_1=-2,\ x_2=4)$. A primeira comparação que temos que fazer é se o ponto possui $X_2 \geq -0,82$. Vemos que sim, então vamos fazer a busca agora só na parte superior do espaço.

Código - Imagem

from matplotlib import patches
fig, axes = plt.subplots(figsize=(8,6))
axes.add_artist(patches.Rectangle([-7, -0.82], 16, 9.82, facecolor="xkcd:sky blue", alpha=0.2))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.scatter([-2], [4], s=100, c="black")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()
axes.axhline(-0.82,0,1, lw=3, color="xkcd:light grey", ls="dashed")
axes.axvline(0.58, (-0.82+7)/16, 1,lw=3, color="xkcd:light grey", ls="dashed")
axes.axvline(0.25, 0, (-0.82+7)/16,lw=3, color="xkcd:light grey", ls="dashed")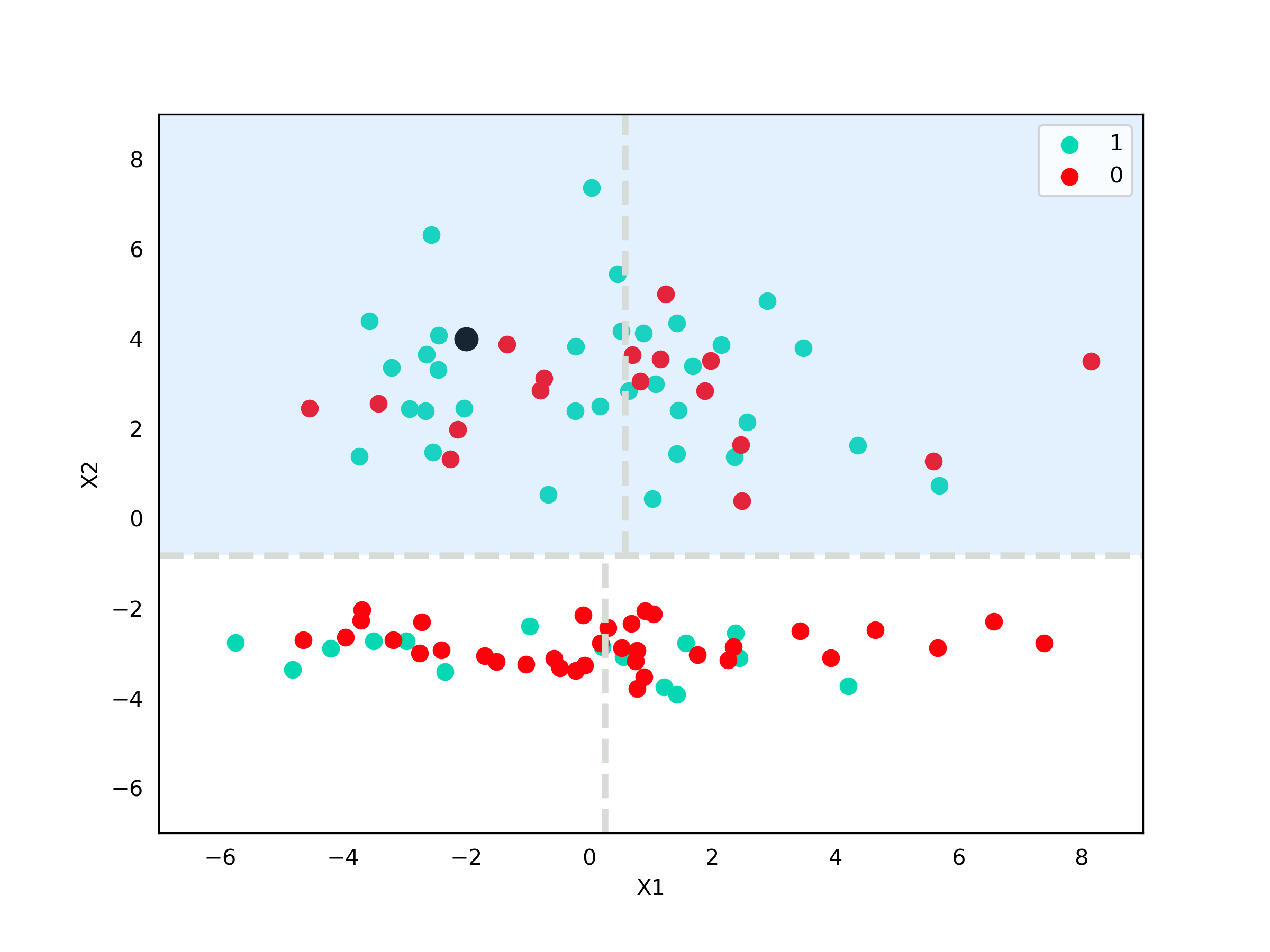

A segunda pergunta que temos que fazer, dado que estamos na parte superior é: $X_1 \geq 0,58$? Podemos ver que não, então nossa região de interesse é a região à esquerda. Agora que não temos mais perguntas, nós chegamos na nossa região de interesse e a nossa busca é feita somente entre esses pontos.

Código - Imagem

fig, axes = plt.subplots(figsize=(8,6))
axes.add_artist(patches.Rectangle([-7, -0.82], 7.58, 9.82, facecolor="xkcd:sky blue", alpha=0.2))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.scatter([-2], [4], s=100, c="black")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()
axes.axhline(-0.82,0,1, lw=3, color="xkcd:light grey", ls="dashed")
axes.axvline(0.58, (-0.82+7)/16, 1,lw=3, color="xkcd:light grey", ls="dashed")
axes.axvline(0.25, 0, (-0.82+7)/16,lw=3, color="xkcd:light grey", ls="dashed")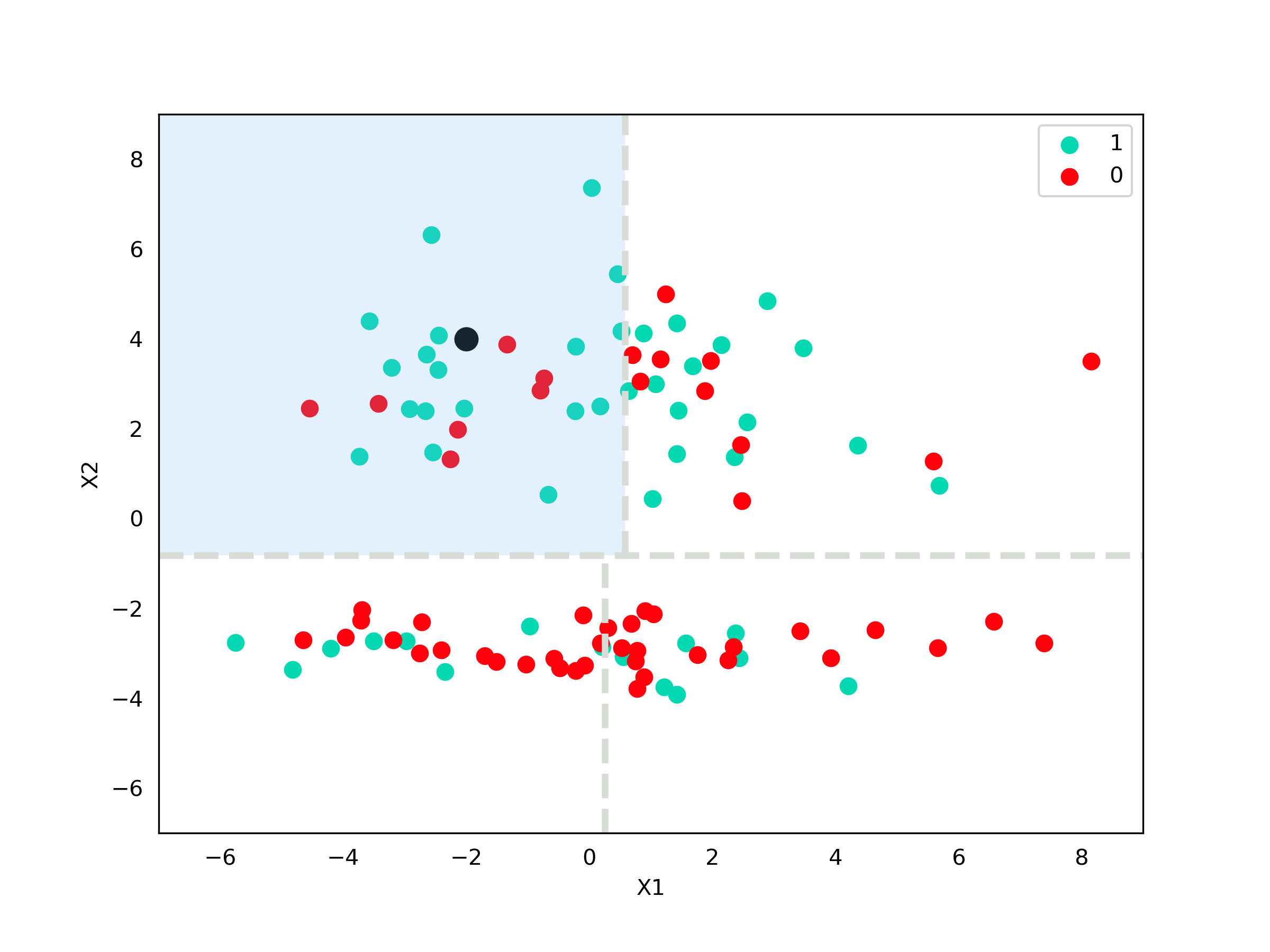

Ball-tree

Assim como as KD-trees, as Ball-Trees particionam o conjunto de dados em conjuntos menores. A diferença é que agora não fazemos mais cortes paralelos aos eixos e sim criamos bolas em K dimensões. Em duas dimensões, essas “bolas” são círculos, em três dimensões são esferas e, a partir de 4 dimensões elas recebem o nome genérico de hiperesferas. Aqui vamos utilizar o termo “bola” para simplificar. A representação final continua sendo uma árvore binária, mas agora o critério de quebra é o pertencimento ou não à bola.

Existem alguns algoritmos para a criação dessas bolas e particionamento do espaço. Aqui temos um deles:

Para o nó atual, encontre o centróide;
Determine o ponto $c_1$ como o ponto mais distante do centroide;
Determine o ponto $c_2$ como o ponto mais distante de $c_1$;
Para todos os outros pontos, determine a bola a que ele pertece calculando $min(d(x, c_1), d(x, c_2))$;
O nó filho da esquerda é a bola com centro $c_1$ e raio $max(d(c_1,x))$ para todo $x$ pertencente a essa bola;
O nó filho da direita é a bola com centro $c_2$ e raio $max(d(c_2,y))$ para todo $y$ pertencente a essa bola;
Para cada nó filho, refaça o passo 1.

Um ponto interessante de se notar é a diferença entre centro e centróide no algoritmo. Quando estamos percorrendo a árvore vamos sempre calcular as distância em relação aos centros. Os centróides só são utilizados para descobrirmos os centros de cada bola. Outro ponto digno de nota é que as bolas podem se cruzar, ou seja, podem existir regiões que pertencem às duas bolas. Isso não é um problema porque o critério que define se vamos para o nó filho esquerdo ou direto de um dado nó pai não é o pertencimento à bola e sim qual dos dois centros é o mais próximo.

Vamos fazer o processo de criação da árvore para ficar mais simples entender. Os dados são os mesmos da seção anterior. A primeira coisa que temos que fazer é calcular o centróide desses pontos. Mas o que é um centróide? O centróide nada mais é que o ponto médio de um conjunto de dados. O seu cálculo é muito simples, basta tirar a média de cada variável do nosso conjunto de dados:

Código - Centróide

print(X.mean(axis=0))

\[\text{centroide}(X_1, X_2) = (0,15;0,04)\]

Código - Imagem

fig, axes = plt.subplots(figsize=(8,6))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.scatter([0.15], [0.04], s=100, c="black")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()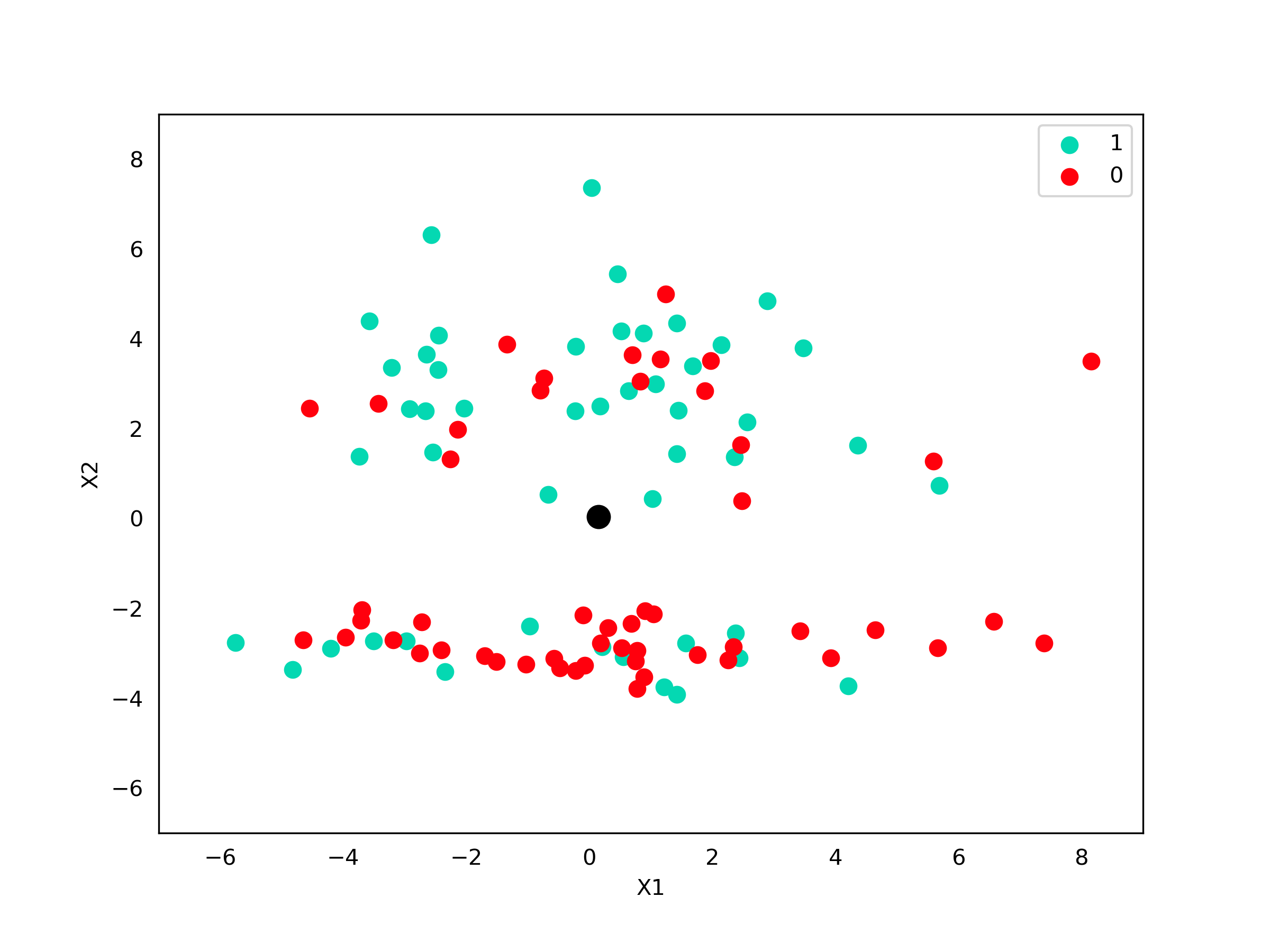

Certo, agora que temos nosso centróide, vamos calcular qual o ponto mais distante a ele. Verificando a distância entre todos os pontos e o centróide, o ponto mais distante está na posição

Código - C1

from scipy.spatial import distance
p = np.array([(0.15, 0.04)])

# Calcula distância de p para todos os pontos em X
distances = distance.cdist(p, X, "euclidean")

# Posição do ponto mais distante à p
idx = np.argmax(distances)

c_1 = X[idx, :]

\[c_1 = (8,16; 3,5)\]

O próximo passo é calcular o ponto mais distante de $c_1$. Utilizando a mesma abordagem de verificar a distância para todos os pontos, chegamos à

Código - C2

# Calcula distância de c1 para todos os pontos em X
distances = distance.cdist([c_1], X, "euclidean")

# Posição do ponto mais distante à c_1
idx = np.argmax(distances)

c_2 = X[idx, :]

\[c_2 = (-5,76; -2,76)\]

Vamos analisar visualmente onde estão esses pontos

Código - Imagem

fig, axes = plt.subplots(figsize=(8,6))
axes.scatter(X[y==1,0], X[y==1,1], c="xkcd:aquamarine", s=50, label="1")
axes.scatter(X[y==0,0], X[y==0,1], c="xkcd:bright red", s=50, label="0")
axes.scatter(p[0, 0], p[0,1], s=100, c="black")
axes.scatter(c_1[0], c_1[1], s=100, c="xkcd:tangerine")
axes.scatter(c_2[0], c_2[1], s=100, c="xkcd:sky blue")
axes.text(8.16, 2.5, "$c_1$", size=15, va="center", ha="center")
axes.text(-5.76, -2, "$c_2$", size=15, va="center", ha="center")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))
axes.legend()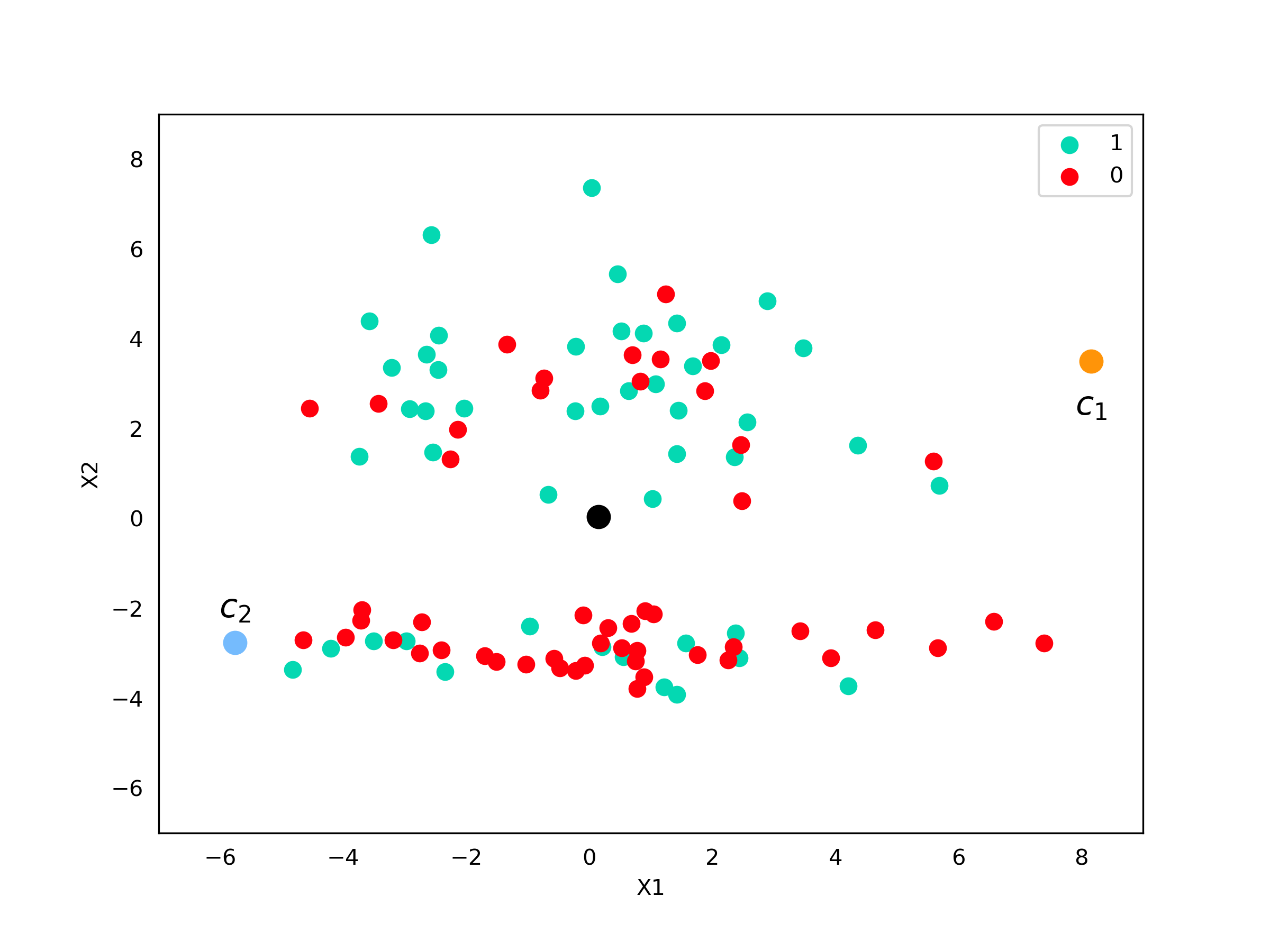

Ótimo! Já temos os nosso centros! Agora é só verificar, para cada ponto, qual centro, $c_1$ ou $c_2$, é o mais próximo.

Código - Imagem

# Calcula a distância de todos os pontos para c_1
d_1 = distance.cdist([c_1], X, "euclidean").squeeze()

# Calcula a distância de todos os pontos para c_2
d_2 = distance.cdist([c_2], X, "euclidean").squeeze()

# Obs: a função squeeeze é usada para transformar o vetor de 2 dimensões para 1
# bola é um vetor booleano que me diz se um ponto pertence à bola 1 ou não 
bola = d_1 <= d_2
                
# Calcula a distância máxima dos pontos mais próximos a c_1
dmax_1 = distance.cdist([c_1], X[bola], "euclidean").squeeze().max()

# Calcula a distância máxima dos pontos mais próximos a c_1
dmax_2 = distance.cdist([c_2], X[~bola], "euclidean").squeeze().max()

# Plota imagem
fig, axes = plt.subplots(figsize=(8,8))
axes.add_artist(plt.Circle((c_1[0], c_1[1]), dmax_1, fill=False, edgecolor="xkcd:tangerine", ls="dashed"))
axes.add_artist(plt.Circle((c_2[0], c_2[1]), dmax_2, fill=False, edgecolor="xkcd:sky blue", ls="dashed"))
axes.scatter(X[bola,0], X[bola,1], c="xkcd:tangerine", s=50, label="1")
axes.scatter(X[~bola,0], X[~bola,1], c="xkcd:sky blue", s=50, label="0")
axes.scatter(c_1[0], c_1[1], s=100, c="xkcd:tangerine")
axes.scatter(c_2[0], c_2[1], s=100, c="xkcd:sky blue")
axes.text(8.16, 2.5, "$c_1$", size=15, va="center", ha="center")
axes.text(-5.76, -2, "$c_2$", size=15, va="center", ha="center")
axes.set_xlabel("X1")
axes.set_ylabel("X2")
axes.tick_params(bottom=False, left=False,)
axes.set_xlim((-7,9))
axes.set_ylim((-7,9))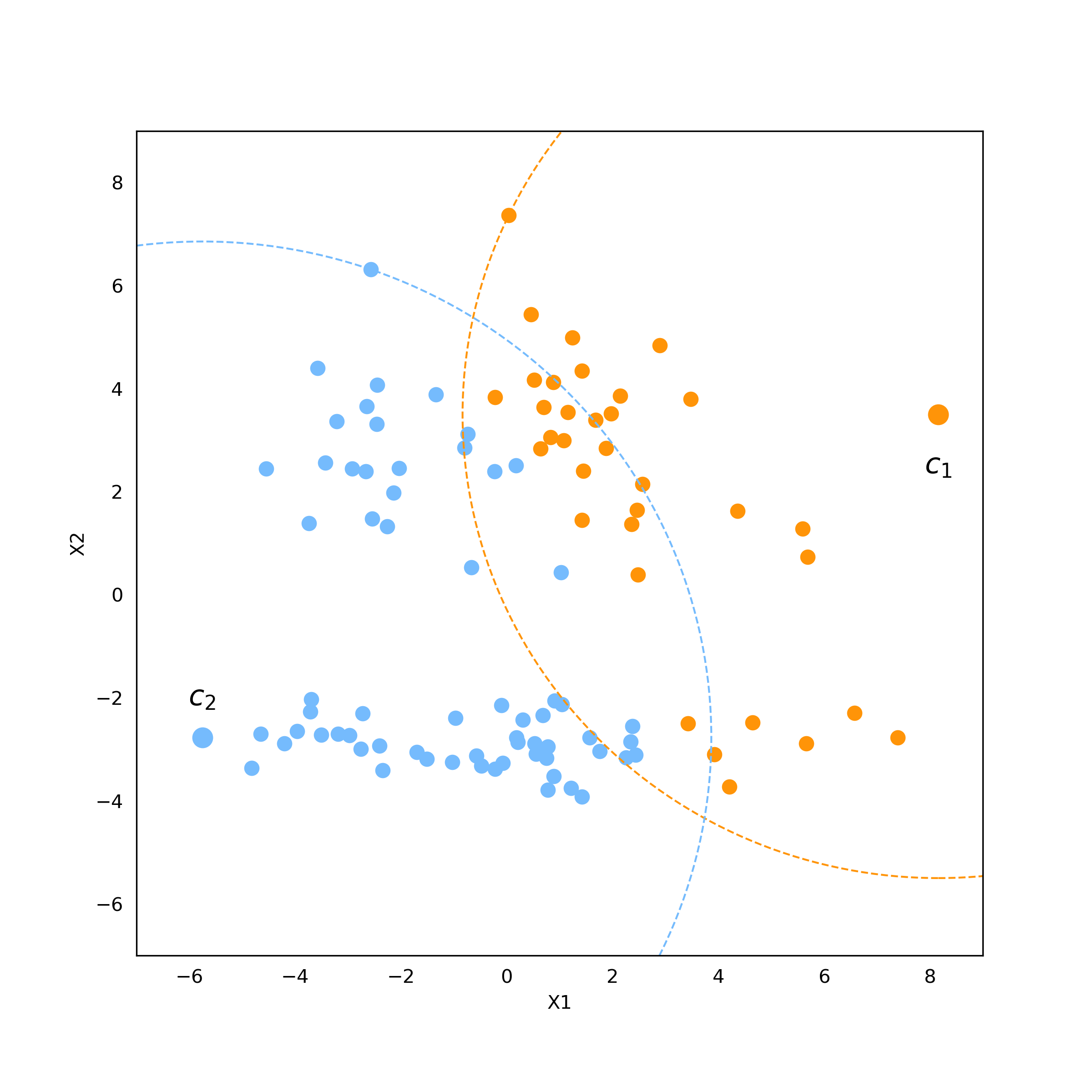

Perceba que as bolas se cruzam e existem pontos azuis que estão dentro da bola laranja e pontos laranjas que estão dentro da bola azul. Como dissemos antes, isso não é um problema dado que a quebra é feita de acordo com o centro mais próximo. Da mesma forma que fizemos com a KD-Tree, podemos realizar o processo de novo dentro de cada uma das bolas criadas e ir criando bolas dentro das bolas. A ideia da busca é muito similar também: verificamos qual o centro mais próximo em cada nó e vamos percorrendo a árvore dessa forma até chegar no último nível. A busca de vizinhos então é feita somente entre os pontos que caíram na mesma bola que nosso ponto de interesse.

E agora? O que eu uso?

Tá … mas você pode estar se perguntando “Quando eu posso usar o algoritmo de força-bruta?” ou “Se eu não puder usá-lo, qual dos dois índices eu uso?”. Essas são ótimas dúvidas e, de maneira geral, podemos seguir as seguintes convenções:

Se você tem poucos dados (ou uma quantidade suficientemente pequena para que tempo não seja um problema), pode-se utilizar o algoritmo de força-bruta;
Quando o tempo de busca de vizinhos é um problema, já é hora de usar um índice:
1. Se você tem poucas variáveis, o mais indicado é a KD-Tree, pois seu algoritmo de construção é mais rápido e ela tem uma boa performance em baixas dimensões;
2. Quando você tem um grande número de variáveis, a performance das KD-Trees começa a cair (precisamos de muitos cortes, ou seja, uma árvore muito profunda para atingir uma boa segregação). Nesse caso, o ideal é usar a Ball Tree.

Conclusão

Com esse artigo, concluímos nossa explicação sobre o KNN. Alguns artigos foram mais voltados a questões mais amplas do que o próprio KNN, como o de Viés e Variância. Porém ele é ideal para introduzir conceitos mais complexos, por ser um algoritmo simples de entender, que continuam valendo quando falamos de algoritmos mais “poderosos” como Gradient Boosting ou Redes Neurais. Espero que tenham gostado dessa série e nos vemos em breve!

Alexandr.IA

Índices

Índices

O que é um índice?

Por que precisamos de índices?

O que isso tem a ver com o KNN?

KD Tree

Ball-tree

E agora? O que eu uso?

Conclusão

Quem bate sou eu!

Matheus Jorge

Índices

Índices

O que é um índice?

Por que precisamos de índices?

O que isso tem a ver com o KNN?

KD Tree

Ball-tree

E agora? O que eu uso?

Conclusão

Quem bate sou eu!

Share

Matheus Jorge