8 min de leitura
K vizinhos mais próximos

K vizinhos mais próximos
Fala, pessoal! Depois da nossa série sobre redes neurais, estamos de volta para falar sobre outro tipo de algoritmo de machine learning: o K vizinhos mais próximos (ou KNN, do inglês K Nearest Neighbors). O KNN é um algoritmo relativamente simples na intuição. Podemos descrever o seu funcionamento em duas etapas:
- Encontrar os K elementos mais parecidos (vizinhos) com o elemento que queremos saber a resposta;
- Sumarizar a reposta (já conhecida) desses elementos vizinhos para obter a predição para o elemento desejado.
Intuitivamente, o KNN utiliza a máxima de que elementos com características similares, ou seja, elementos parecidos, tendem a ter a mesma resposta. Isso faz sentido se pensarmos no nosso dia a dia: nossos amigos e familiares com quem temos mais afinidade (mais parecidos) tendem a ter as mesmas opiniões e interesses que nós. Uma outra forma de se lembrar da intuição desse algortimo é pela famosa frase:
“Diga-me com quem andas que te direi quem tu és”
Mas, mesmo com uma intuinção tão simples, os dois passos descritos acima deixam algumas dúvidas (pare um pouco agora antes de prosseguir e veja se consegue pensar em alguma coisa que não está bem definida). Se você já fez sua reflexão, podemos prosseguir com as dúvidas que me vêem à mente:
- O que significa “sumarizar” as reposta dos vizinhos?
- Como medimos o quão parecido dois elementos são?
- Qual o melhor valor de K? O que muda quando temos um K muito pequeno ou muito grande?
Essas são as principais perguntas que pretendemos responder ao longo dessa nova série. Sem mais delongas, vamos ao que interessa!
Previsões
Pelo passo a passo, o KKN não possui uma etapa de treino propriamente dita, como as redes neurais, mas ainda queremos que ele nos dê uma previsão, certo? Um ponto importante aqui é que, apesar de não haver um treino explícito, ainda precisamos de um conjunto de dados de treino (dos quais sabemos as respostas) para conseguir realizar uma previsão para outros dados. O passo a passo do algoritmo é bem intuitivo sobre o que devemos fazer para obtermos essas previsão. Mesmo assim, existem alguma dúvidas no ar sobre como realmente fazer essa previsão nos dois passos. Aqui vamos inverter um pouco a ordem e começar falando sobre o passo 2: sumarizar as respostas dos vizinhos. Mas o que significa sumarizar as respostas? Quando utilizamos “sumarizar”, estamos nos referindo ao fato de pegar um conjunto de pontos (as respostas dos vizinhos) e retornar um único número (a saída prevista). Vamos tratar esse assunto de dois pontos de vista: classificação e regressão.
Classificação
Começaremos falando sobre classificação. Só recapitulando um pouco, quando nos referimos à “classificação”, queremos dizer que nosso problema nos pede para prever uma saída discreta, também chamadas de classes. Por exemplo, se temos uma imagem e queremos saber se trata-se de um cachorro, um gato ou um passáro, esses são os únicos 3 valores que podemos admitir na saída. Outro exemplo clássico é quando temos um e-mail e queremos saber se é um spam ou não.
Nesse cenário, o modo mais intuitivo de fazer a sumarização é simplemente contando quantos elementos de cada classe são meus vizinhos. A classe com mais vizinhos será a nossa previsão.
Vamos usar o exemplo do spam aqui. Suponha que tenhamos um conjunto de e-mails que já sabemos se são spam (verdes) ou não (vermelhos). Quando o novo e-mail $A$ chega, queremos saber se ele é ou não spam. Para isso procuramos os e-mails mais parecidos com $A$ e vemos suas repostas. A imagem a seguir pode ajudar a entendermos melhor:
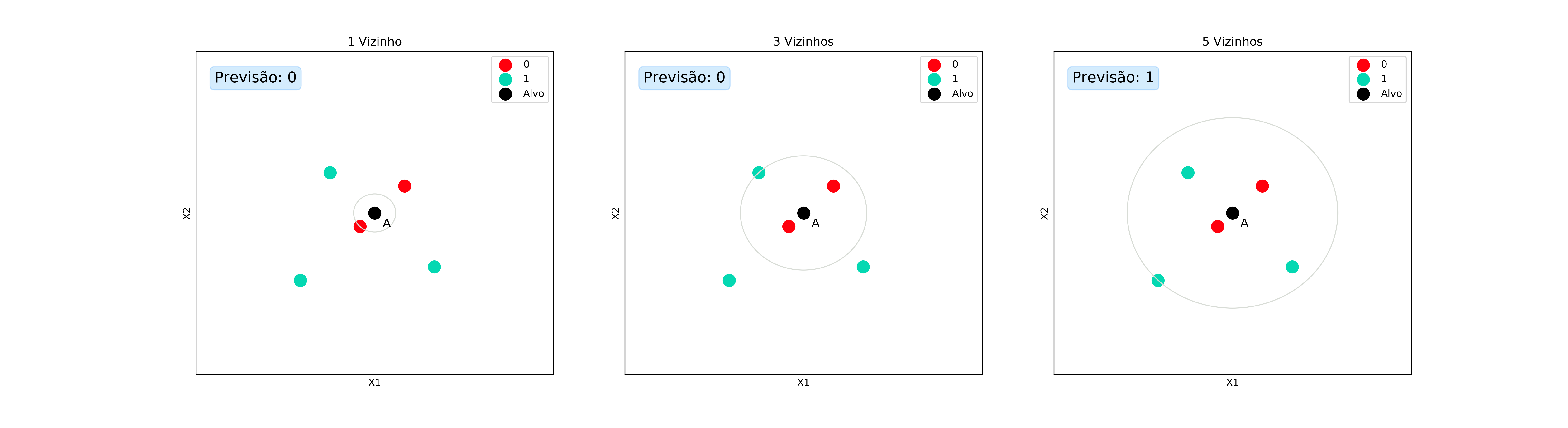
Podemos também ir um pouco mais além e dizer também qual a probabilidade daquele e-mail ser spam. Em vez de apenas pegar a classe com mais representantes, vamos agora analisar a quantidade de vizinhos de cada classe dentre os K mais próximos. Matematicamente, podemos escrever essa probabilidade como:
\[P(Y=j|X=x_A) = \frac{1}{K} \sum_{i \in N_A} I(y_i = j)\]Espera um pouco! Estavámos falando aqui de vizinhos, com imagens bonitinhas e agora temos essa equação feia? Em uma primeira olhada ela pode parecer realmente estranha, mas vamos analisá-la com mais calma. Primeiro algumas definições:
- $x_A$: conjunto de características do ponto A;
- $P(Y=j \vert X=x_A)$: probabilidade do ponto A pertencem à classe j;
- $K$: quantidade de vizinhos que estamos analisando;
- $N_A$: conjunto dos $K$ vizinhos do ponto A;
- $I(y_i = j)$: função que retorna o valor 1, se o ponto $x_i \in N_A$ pertencer à classe j ($y_i = j$), e 0, caso contrário.
Começando pela parte do somatório: para cada um dos vizinhos do ponto A, verificamos se ele percentece à classe j. Caso ele pertença, o valor do somatório é acrescido de 1. Caso ele não pertença, o somatório continua com o mesmo valor. Ou seja, o somatório indica quantos dos K vizinhos pertencem à classe j. Quando dividimos por $K$, o que estamos fazendo é encontrar a proporção de vizinhos que pertencem à classe j. É essa proporção que vamos considerar como a nossa probabilidade.
De novo, vamos recorrer às imagens para trazer um entendimento melhor.
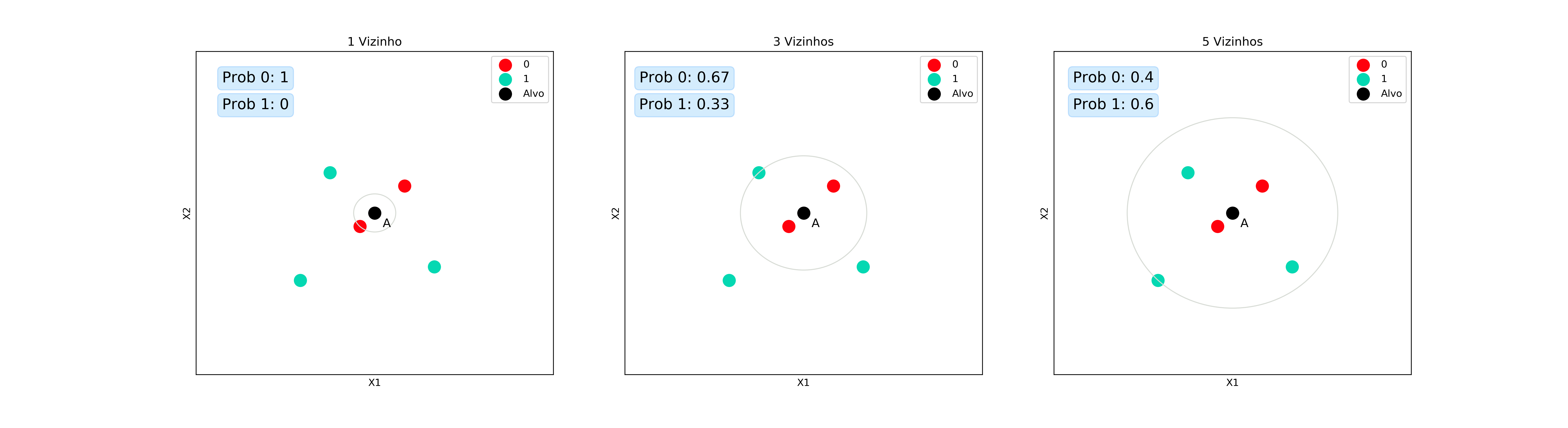
Que legal! Conseguimos até estimar as probabilidades de pertencimento à determinada classe, mas aqui vou levantar outro questionamento (lá vem ele de novo): o que acontece com a noção de distância mesmo entre os vizinhos? Nos nossos exemplos, os vizinhos mais próximos do ponto A são da classe 0, mas mesmo assim, quando escolhemos $K=5$, a previsão que temos é da classe 1. Dessa forma, descartamos totalmente a informação das diferentes distâncias e tratamos todos os vizinhos como iguais.
Uma forma de considerarmos essa relação entre os vizinhos é atribuindo um peso $w_i$ ao voto de cada vizinho.
\[P(Y=j|X=x_A) = \frac{\sum_{i \in N_A} w_i I(y_i = j)}{\sum_{i \in N_A} w_i}\]Uma maneira simples de fazer isso é considerando o inverso da distância entre os pontos:
\[w_i = \frac{1}{d(x_A,x_i)}\]na qual $d$ é uma medida de distância entre as amostras. Novamente, a equação pode parecer complicada mas, na verdade, o que estamos fazendo é dar um valor ao voto de cada vizinho, em vez de sempre considerar esse valor 1.
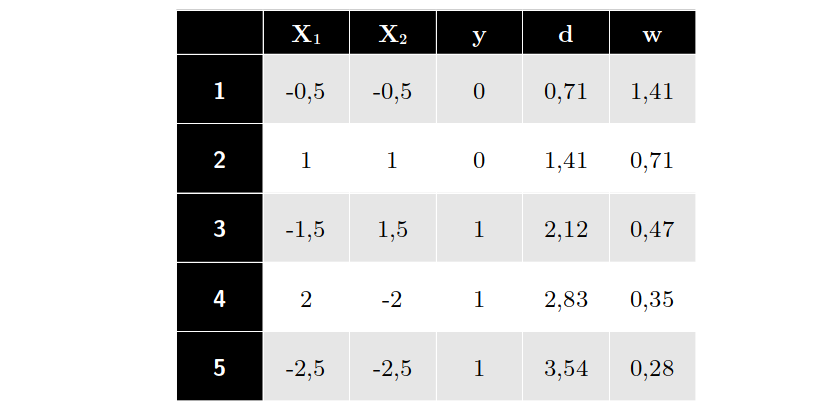
Os dados do nosso exemplo são os seguintes, já com distâncias e pesos calculados para o nosso exemplo alvo $x_A = (0;0)$
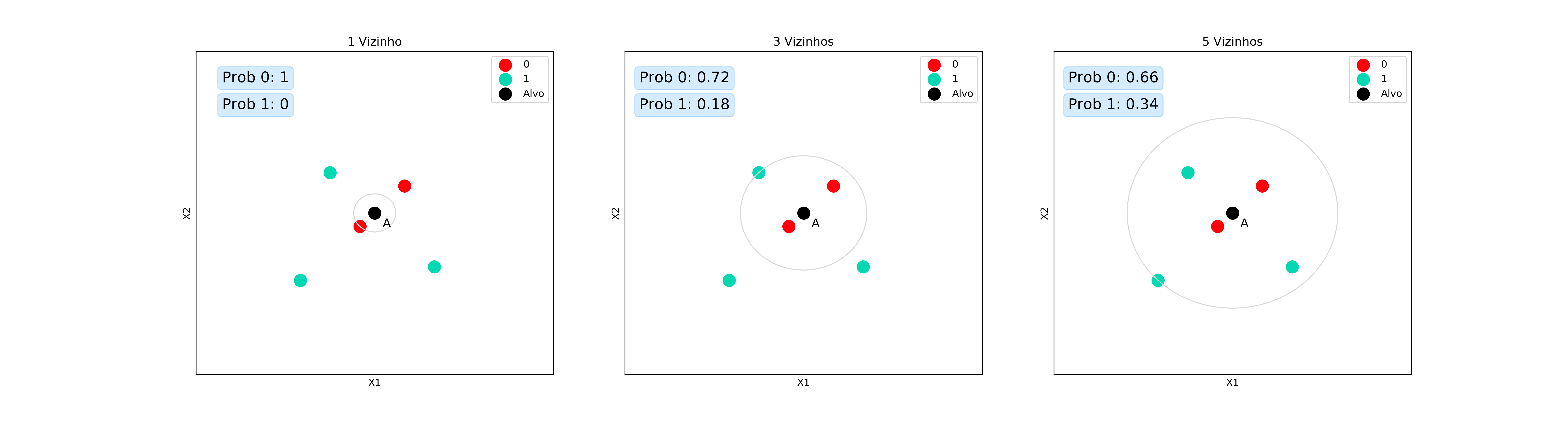
Com isso, podemos estimar as novas probabilidades:
Regressão
Agora que já vimos como a classificação é feita, vamos dar uma olhada no nosso outro tipo de problema: a regressão. A diferença para a classifcação é que agora queremos prever uma variável contínua. Por exemplo, podemos querer saber o preço de uma casa dada a sua área e a sua localização ou saber a temperatura de uma cidade da qual não temos medições baseado nas cidades vizinhas.
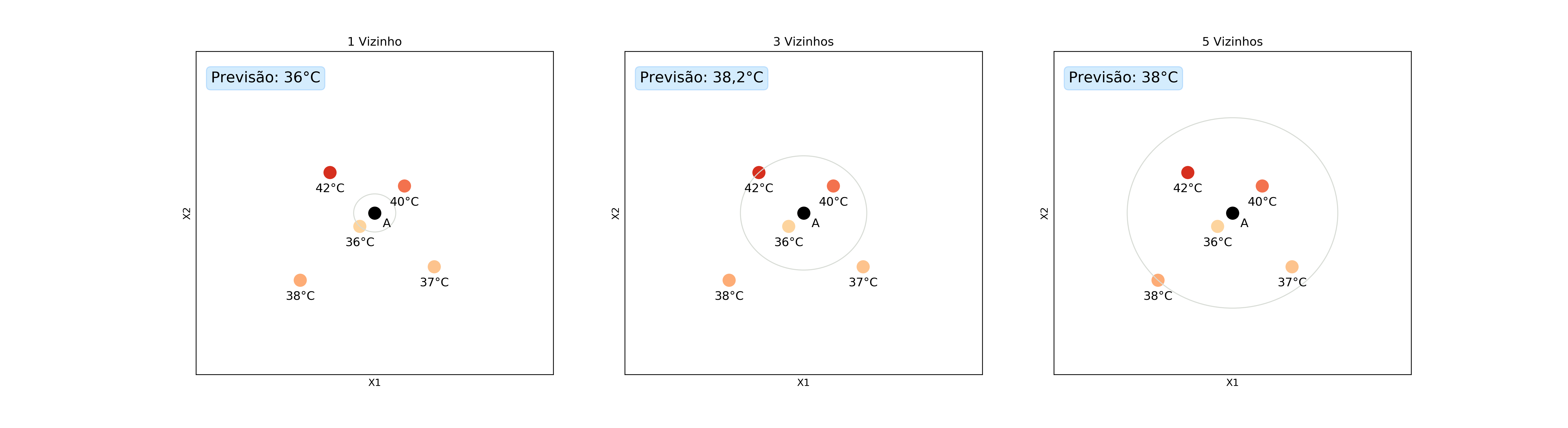
A abordagem de usar a moda agora não é mais adequada, pois, muito provavelmente, as respostas não serão mais repetidas, uma vez que eles podem assumir uma quantidade ilimitada de valores. Uma solução é usar a média das respostas dos vizinhos. Vamos usar o exemplo da temperatura para ilustrar esses conceitos.
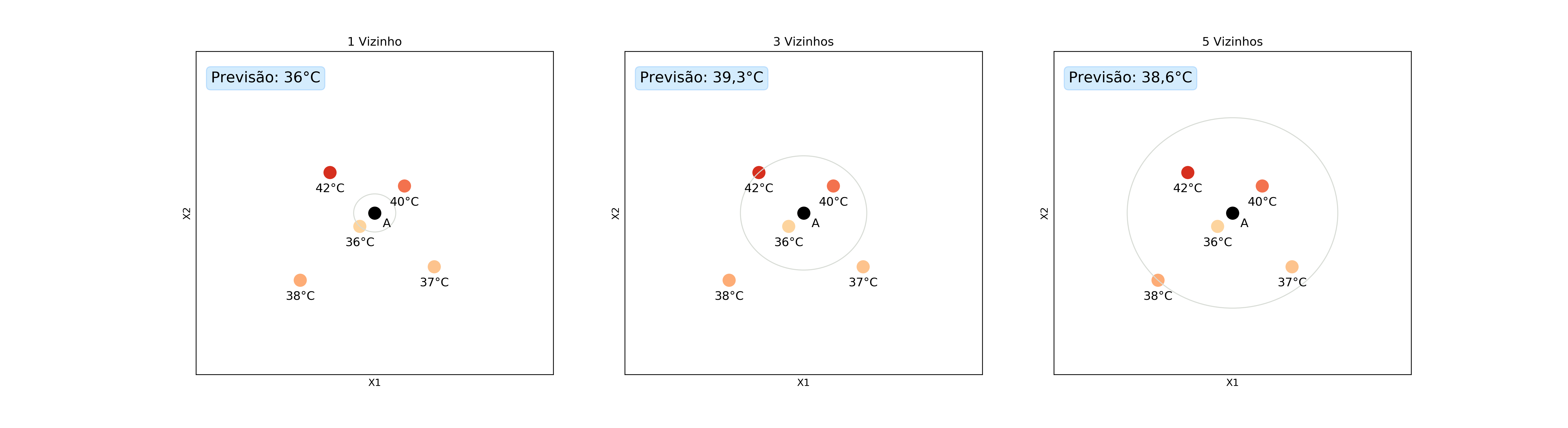
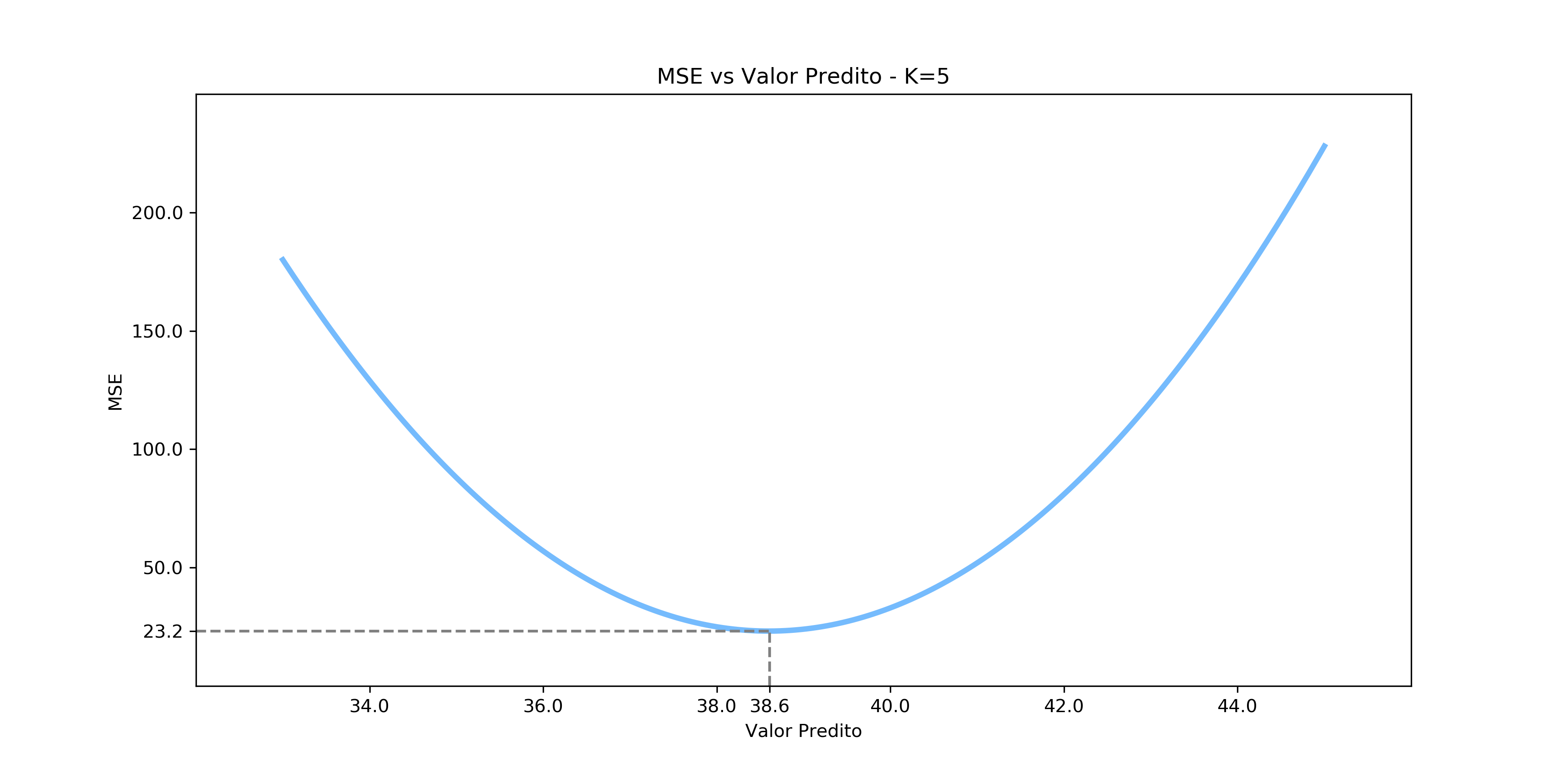
Perceba que nenhum dos vizinhos tem exatamente a mesma temperatura e, por isso, não podemos usar a moda. Mas porque usar a média então? Porque não o valor máximo? Ou o valor mínimo? Essa escolha é feita pelo fato de que a média de um conjunto de pontos é o valor que minimiza o erro quadrático médio (MSE, do inglês mean squared error):
\[\frac{1}{n}\sum_{i=1}^{n} (x_i - \hat{x})^2\]Visualmente, podemos ver como o erro varia quando utilizamos outros valores para a previsão. Em nenhum caso retratado na imagem abaixo conseguiríamos um erro menor do que a previsão dada pela média.
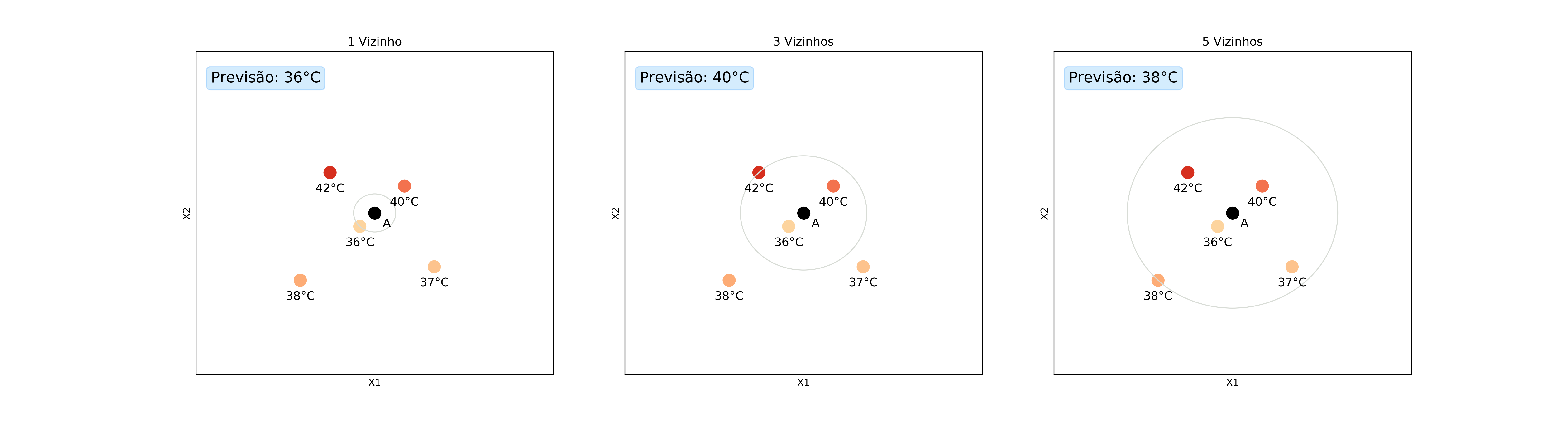
Mas e se não quisermos minimizar o MSE? Nesse caso podemos escolher o valor que melhor se adequa à função de erro de nosso interesse. Por exemplo, caso escolhêssemos a mediana, estaríamos minimizando o erro absoluto médio (MAE, do inglês mean absolute error):
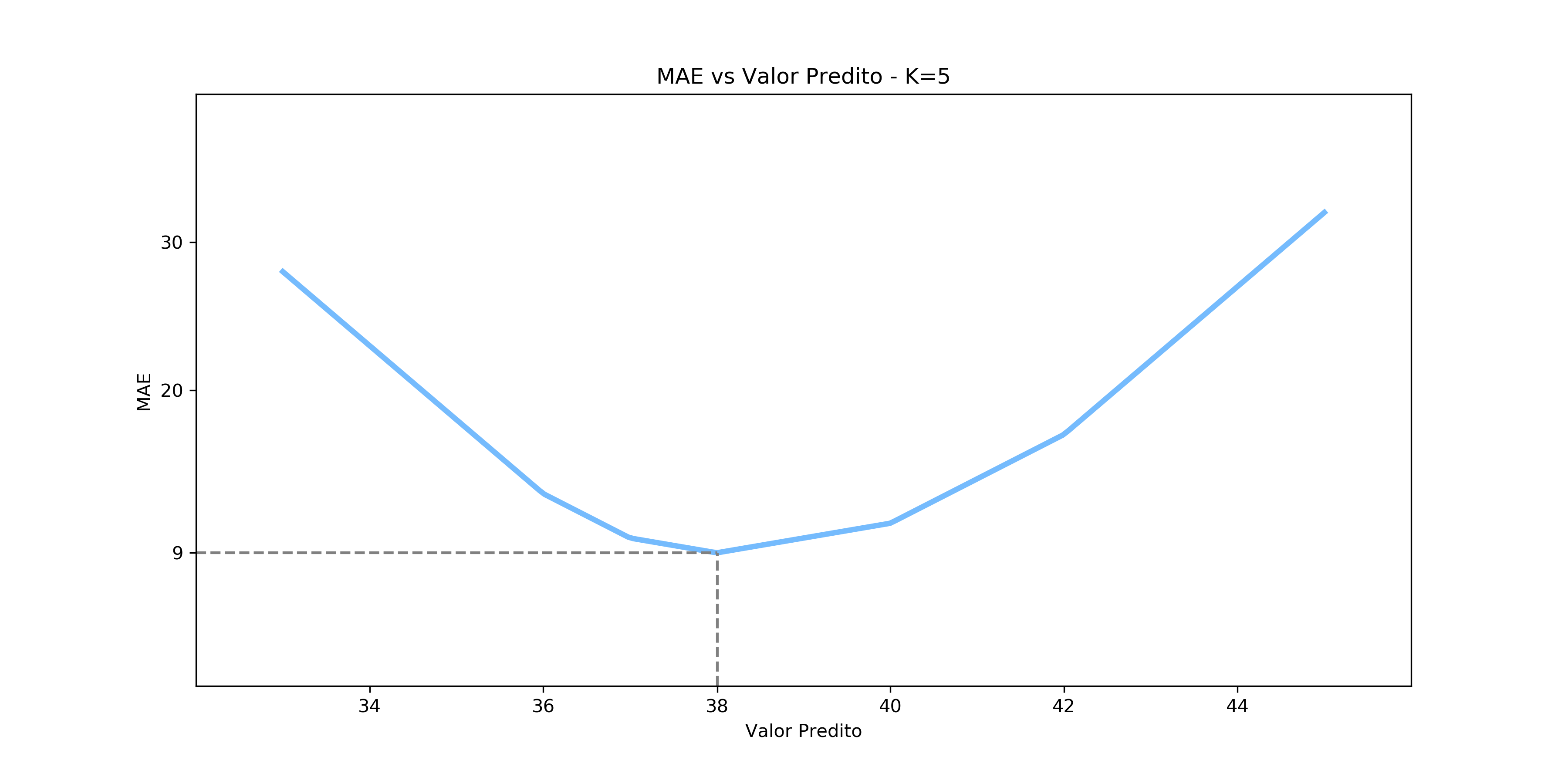
\[\frac{1}{n}\sum_{i=1}^{n} |x_i - \hat{x}|\]Vamos ver como ficariam as previsões nesse caso:
Novamente, podemos checar graficamente que nossa afirmação é verdadeira:
Por fim, vamos fazer exatamente o que fizemos no caso da classificação e incluir um peso para a contribuição de cada vizinho, baseado na distância entre o meu ponto alvo e cada um deles. A motivação é exatamente a mesma também: vizinhos mais distantes deveriam ter um peso menor na minha resposta do que vizinhos mais próximos.
Para facilitar um pouco, vamos dizer que os pontos estão nas mesmas posições em que estavam no problema de classificação. Dessa forma, a tabela que mostramos acima continua valendo, assim como o peso de cada amostra.
Conclusão
Wow, foi muita coisa não é mesmo? Vimos um pouco da intuição por trás do KNN e como ele realiza previsões, tanto para problemas de classificação quanto de regressão. Apesar de denso, espero que o conteúdo tenha sido proveitoso.
O próximo artigo vai tentar responder a questão sobre qual é o número ideal de vizinhos e fazeremos uma discussão sobre dois conceitos fundamentais em aprendizado de máquina: viés e variância. Até lá, pessoal!

