13 de Setembro de 2021 9 min de leitura

Viés e Variância

Viés e Variância

Fala, pessoal! Estamos de volta para falar sobre o algoritmo KNN (os K vizinhos mais próximos). No último artigo, nós apresentamos a intuição do algoritmo e discutimos as diferentes maneiras de darmos as predições, tanto em modelos de classificação quanto de regressão.

Hoje vamos discutir um dos pontos que gera mais dúvida no modelo: o que muda quando variamos o valor de K (o número de vizinhos).

Viés e variância

Antes de entrarmos na discussão de como o valor de K muda as resposta do algoritmo, vamos ver dois conceitos super importantes em aprendizado de máquina: viés e variância.

Vamos começar pelo viés (bias em inglês). A definição que eu acho mais intuitiva é

viés é a capacidade que o modelo tem de aprender.

Essa capacidade vem do conjunto de suposições que fazemos ao escolher determinado modelo para explicar nossos dados, ou seja, é o quanto da nossa crença colocamos no modelo. Por exemplo, escolhendo um modelo de regressão linear simples, estamos supondo que a relação entre minhas variáveis explicativas e a minha variável alvo é somente linear (ou seja, toda vez que a variável explicativa aumenta 1 unidade, a variável alvo aumenta um certo valor $\beta$). Se a relação entre elas for diferente disso, o meu modelo vai performar mal por causa das minhas suposições iniciais.

Vamos supor que estamos interessados em prever o preço de um imóvel baseado na sua área e no número de quartos. Vamos também supor que nós temos um conjunto $\mathcal{F}$ de todas as possíveis funções $f(\text{area}, \text{quartos}) \rightarrow \mathbb{R}$ que mapeiam as entradas na saída esperada, que é o preço. Esse conjunto é normalmente denominado espaço de hipóteses.

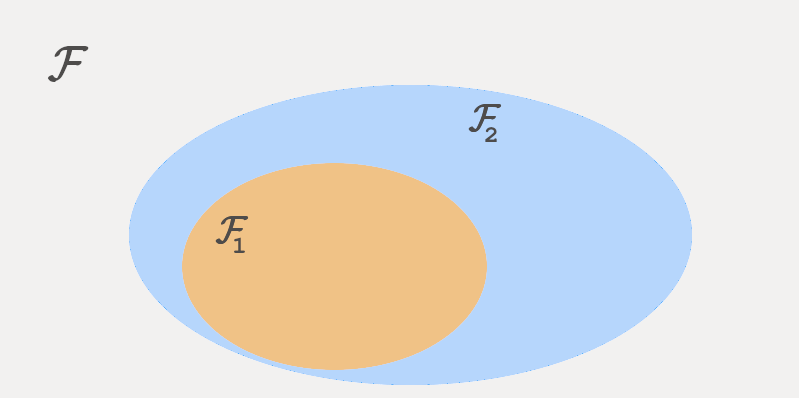
Dentro do conjunto $\mathcal{F}$, podemos selecionar um subconjunto $\mathcal{F}_1$. Vamos fazer $\mathcal{F}_1$ ser o conjunto de todas as funções lineares, ou seja,

Um problema dessa equação é que ela não considera que pode haver alguma interação entre as variáveis: perceba como os termos que contêm a área e os quartos são indenpendentes um do outro. Vamos fazer uma brincadeira aqui e selecionar um segundo subconjunto $\mathcal{F}_2$, cujas funções tem o seguinte formato:

Perceba que, fazendo $\beta_3 = 0$, $\mathcal{F}_1$ e $\mathcal{F}_2$ seriam o mesmo conjunto. Isso quer dizer que todas as equações de $\mathcal{F}_1$ estão contidas em $\mathcal{F}_2$. Porém $\mathcal{F}_2$ pode ir ainda mais além: fazendo $\beta_3 \neq 0$, temos um conjunto ainda mais amplos de funções.

Quanto maior o número de funções que meu modelo puder assumir, menor é o seu viés, ou seja, eu estou fazendo menos suposições prévias sobre as relações dos dados. Voltando ao exemplo do modelo de Regressão Linear (ou seja, as funções do conjunto $\mathcal{F}_1$), eu assumo que

1. minhas variável de saída (preço) tem um dependência linear com as variáveis de entrada (área e quartos);
2. a relação entre elas não impacta a saída.

Se eu utilizar um modelo que possibilita que eu aprenda as funções de $\mathcal{F}_2$, eu ainda faço a suposição número 1, mas eu relaxo a suposiçao número 2: agora quem decide se a relação entre as variáveis impacta ou não a saída é o próprio modelo (através de $\beta_3$). Desse modo, eu precisei incluir menos conhecimento prévio no modelo.

Uma analogia que pode ser interessante para fixar o conhecimento é que o viés me diz o quão “cabeça dura” meu modelo é. Suponha que estamos viajando de carro e a pessoa que está dirigindo tem algumas suposições de como chegar até nosso destino. No meio do caminho temos várias placas indicando qual o melhor caminho. Podemos entender um modelo com alto viés como o motorista “cabeça dura” que ignora todas as placas e acredita que o melhor caminho é aquele que condiz com suas suposições prévias. Quanto mais o motorista seguir as placas, menos viés ele tem.

Olhando dessa forma pode parecer que sempre ter um viés menor é a melhor opção. Mas existe um problema: quanto menos suposições eu fizer sobre o meu modelo, a tendência é que esse modelo se torne mais complexos. Quando eu tenho modelos muito complexos eu preciso de muitos dados para ter uma estimativa precisa dos parâmetros.

Vamos analisar um caso extremo: vamos supor que temos um modelo (mágico) que pode gerar qualquer função de $\mathcal{F}$ (ou seja, um modelo com nenhum viés). Como esse modelo pode assumir qualquer função, para qualquer conjunto de dados de treino que eu passar pra ele, ele vai conseguir gerar um modelo perfeito para aqueles dados, ou seja, o erro de treino desse modelo sempre é 0.

Parece um sonho certo? Antes de sair tentando encontrar esse Santo Graal dos modelos, vamos dar uma olhada mais afundo o que isso significa. Continuando com nosso exemplo de previsão de preço, vamos analisar dois cenários:

1. Extraímos um conjunto de dados $X_1$ e nesse conjunto temos que uma casa com 200 $m^2$ e 4 quartos custa R$ 500.000,00;
2. Alguém nos enviou um segundo conjunto de dados $X_2$. Nesse conjunto temos exatamente as mesmas medições que em $X_1$ mas a casa de 200 $m^2$ e 4 quartos que custa R$ 450.000,00;

Como o modelo se ajusta perfeitamente aos dados, se treinarmos dois modelos diferentes $M_1$ e $M_2$ com cada um dos conjuntos, o modelo $M_1$ vai me dizer um preço (500 mil reais) e o modelo $M_2$ vai me dizer outro (450 mil reais). Mas qual dos dois está certo?

A resposta é: os dois. E nenhum. Como eu não assumi nada, o meu modelo faz o que ele pode com os dados que ele tem. Por esse motivo, eu tenho que passar uma grande quantidade de dados para ele, para cobrir todos os casos possíveis.

Essa mudança nos parâmetros e na previsão do modelo é chamada de variância. Um modelo com alta variância apresenta muitas mudanças de comportamento quando apresentamos dados ligeiramente diferentes para ele no treino. Um modelo com pouca variância consegue se manter estável com pequenas modificações nos dados.

Como todo mundo gosta de uma boa analogia, um modelo com alta variância é como aquela pessoa que não consegue se decidir nunca. Sempre que alguém fala alguma coisa diferente para ela, ela muda de opinião.

Trade-off

Normalmente temos que ponderar esses dois conceitos ao escolher um modelo. Modelos com baixo viés possuem muita variância enquanto modelos com alto viés possuem menor variância.

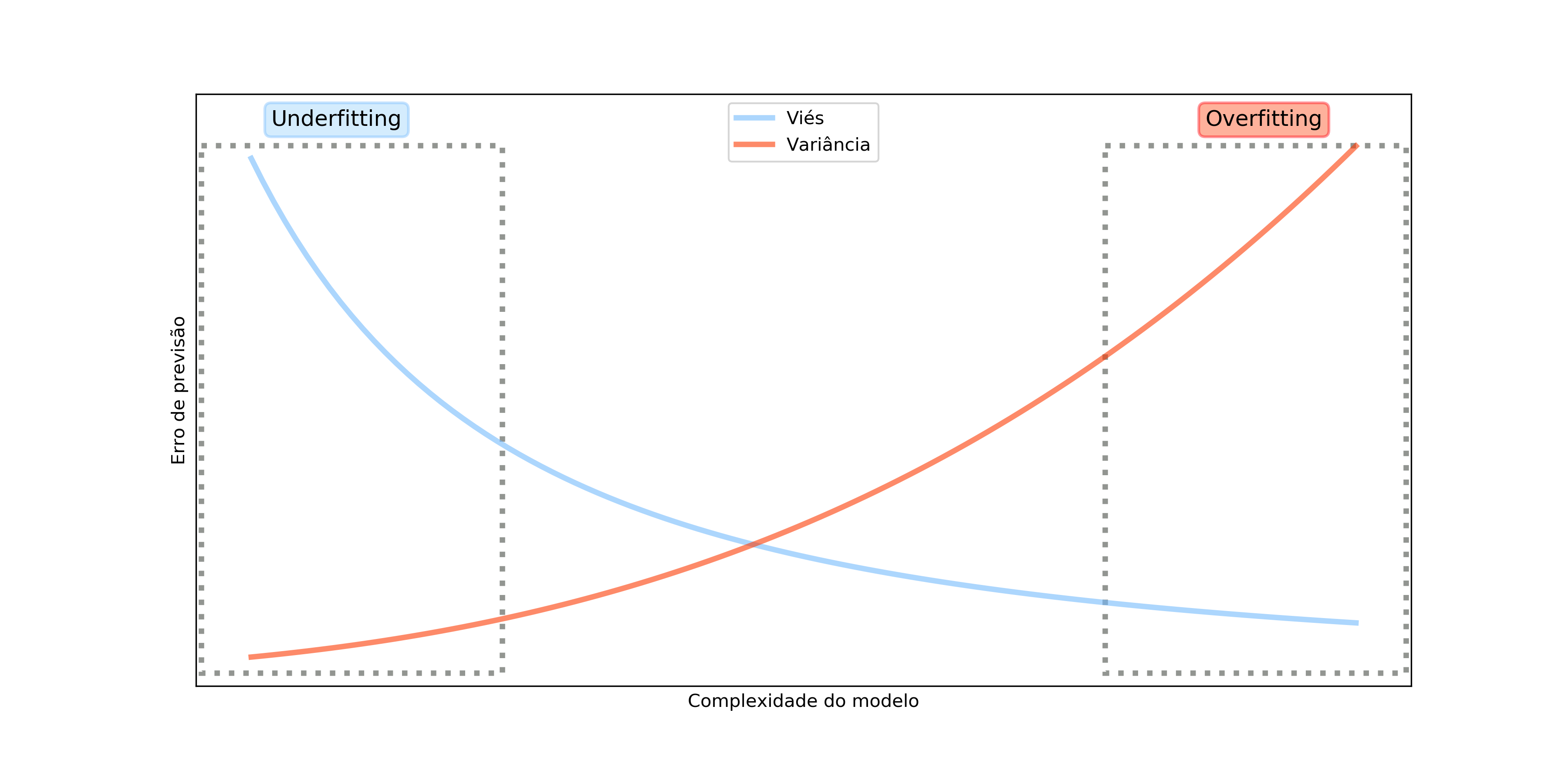
O ideal é evitar modelos nos dois extremos. Modelos com viés muito alto podem não se ajustar bem nem aos dados de treino, porque nossas suposições não condizem com a realidade dos dados. Nesse caso, temos o chamado sub-ajuste (do inglês underfitting).

Na outra ponta, modelos com baixo viés podem se ajustar demais aos dados de treino e,quando forem apresentados a dados novos, não performarem bem. Esse caso é o chamado sobre-ajuste (do inglês overfitting)

E o que isso tem a ver com o valor de K?

Agora que entendemos o que é viés e variância, fica o questionamento: como isso se relaciona com o valor de K?

Vamos analisar um problema bem simples em que temos que prever se um apartamento tem alta procura no mercado (classe 1) ou não (classe 0), utilizando somente dados de latitude e longitude. Aqui estamos tratando de um problema de classificação, mas os resultados e conclusões são exatamente os mesmos para os problemas de regressão. Vamos dar uma olhada então nesses dados:

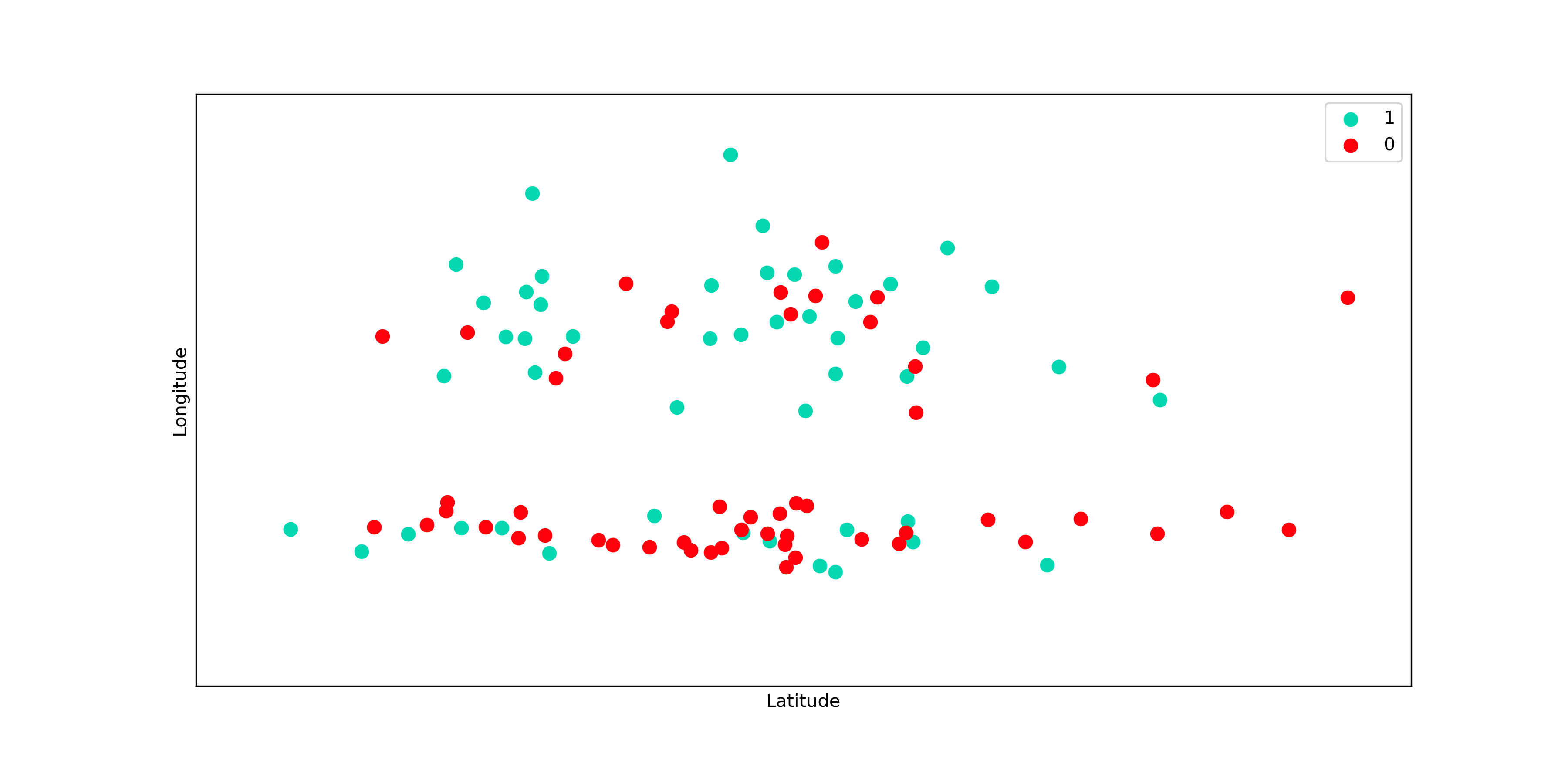
Olhando os dados não parece claro qual seria o valor adequado de K. Vamos então testar alguns valores e ver o que acontece. Na imagem abaixo, temos as fronteiras de decisão para 3 valores diferentes de K: 1, 10 e 50. O gráfico da fronteira de decisão nada mais é do que as regiões em que minhas predições são de cada uma das classes.

Observe como a fronteira de decisão quando K=1 é muito mais irregular do que quando K=50. Um modo de medir o viés e a variância de um modelo é justamente verificar visualmente quão irregular é essa fronteira. Isso pode parecer um pouco confuso, afinal falamos de viés e variância em termos de espaços de funções e no KNN não temos as funções definidas explicitamente.

Mesmo que as funções não sejam definidas analiticamente, todos os modelos no fundo são funções que mapeam as entradas nas saídas e as fronteiras de decisão são uma representação visual dessas funções. Fronteiras que tem o comportamento de ter muitas trocas de classes (como o caso quando K=1) apresentam grande complexidade e portanto tem uma variância alta enquanto fronteiras mais “comportadas” tendem a ter um uma variância menor, justamente por serem mais simples.

Para ver como isso é verdade, vamos supor que temos um novo ponto da classe 1 observado e vamos retreinar o modelo com ele. A imagem abaixo mostra as novas fronteiras de decisão. Perceba como a inclusão de um único ponto alterou significativamente a fronteira para quando K=1, mas não para os outros valores. Entrentanto, valores menores de K parecem que se ajustam melhor aos dados

A partir da imagem a cima, podemos chegar a duas conclusões:

1. Um valor de K alto significa um modelo com alto viés e baixa variância;
2. Um valor de K baixo implica um modelo com baixo viés e alta variância.

Nosso trabalho então é realizar testes de modo a escolher um K que não me dê nem underfitting nem overfitting, o que pode ser bem desafiador.

Conclusão

Hoje falamos sobre dois dos conceitos mais fundamentais do aprendizado de máquina e como isso se relaciona com o hiperparâmetro K do KNN. Fique tranquilo se você não entendeu os conceitos de primeira, pois, apesar de fundamentais, eles não são nada simples. No próximo artigo vamos falar um pouco sobre como dizemos que dois pontos são próximos ou não, ou seja, vamos falar de distâncias. Até lá!