14 min de leitura
Funções de ativação
Funções de ativações
Fala, galera! Bem-vindos a mais artigo da série sobre redes neurais. Dessa vez vamos falar um pouco mais afundo das famosas funções de ativação, mostrando algumas das funções mais comumente utilizadas e quais são as características que fazem com elas sejam tão queridas pelos cientistas de dados.
Relembrando
Como falamos no primeiro artigo dessa série (você pode dar uma conferida aqui, caso ainda não tenha visto), as funções de ativação tem duas funções principais nas redes neurais:
- Na camada de saída, a função de ativação é utilizada para mapearmos a saída da combinação linear dos neurônios dessa camada para o domínio esperado;
- A funções de ativação introduzem não-linearidades nas camadas intermediárias que diminuem o viés do modelo como um todo.
Certo … Muito legal, mas o que isso significa na prática? Bom, o primeiro caso é mais fácil de entender: o que você acharia se eu te dissesse que um paciente tem uma probabilidade de 150% de ter câncer? Certamente você me diria que alguma coisa não está certa pois probabilidades tem que estar entre 0 e 100%. A pergunta é então: como eu consigo que minha rede neural entenda que todas as previsões que ela me dá tem que estar nesse intervalo? Como você deve ter imaginado, quem vem nos salvar são as funções de ativação. Podemos utilizá-las para mapear qualquer número que saia da combinação linear final dessa rede em um número no intervalo de 0 a 1, em que se a previsão for 1 indica uma probabilidade de 100%.
O segundo caso é um pouco mais complexo e vamos precisar da ajuda de algumas equações para entendê-lo. Se nos lembramos bem, a equação que mapeia as entradas $X$ (nossas variáveis explicativas) de uma camada da rede para a saída $O$ dessa camada é:
\[O_i = f(W_i^T X_i + b_i),\]em que o sobrescrito i indica o número da camada na rede, f é a função de ativação, b é o chamado vetor de bias e $W_i$ são os pesos da combinação linear daquela camada. Vamos supor que a função f não exista mais:
\[O_i = W_i^T X_i + b_i\]E o que aconteceria se tivéssemos duas camadas consecutivas nesse formato? Vamos dar uma olhada:
\[O_i = W_i^T X_i + b_i\] \[O_{i+1} = W_{i+1}^T O_i + b_{i+1}= W_{i+1}^T (W_i^T X_i + b_i) + b_{i+1}\] \[O_{i+1} = (W_{i+1}^T W_i^T) X_i + (W_{i+1}^T b_i + b_{i+1})\] \[O_{i+1} = W^{\prime T}_{i+1} X_i + b^\prime_{i+1}\]Olhando a última equação acima, podemos ver que a saída da segunda camada nada mais é do que uma combinação linear das entradas da primeira. E isso significa o que exatamente? Significa que, não importam quantas camadas minha rede tenha, a saida dela será sempre uma combinação linear das entradas da rede. Seria a mesma coisa que ter apenas uma camada na rede, o que não é muito legal. Para uma explicação com um pouco mais de detalhes, vocês podem dar uma olhada no link do artigo.
E agora? O que eu uso?
Muito legal, entendemos o porquê de utilizarmos as funções de ativação, mas quais funções eu posso utilizar e qual é mais indicada para cada cenário?
Na teoria, qualquer função diferenciável (aqui tem uma explicação bem legal sobre o assunto) pode ser utilizada. Vamos ver até que funções que não são diferenciáveis, mas que são diferenciáveis “por partes” podem ser utilizadas (mas sem spoilers por agora, já chegamos lá).
Sigmóide
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]Também conhecida como função logística, a função sigmóide é uma das funções de ativação mais utilizadas em redes neurais, principalmente em camadas finais. Será que só de olhar para a forma dessa função você consegue dizer qual a propriedade mais importante dela?
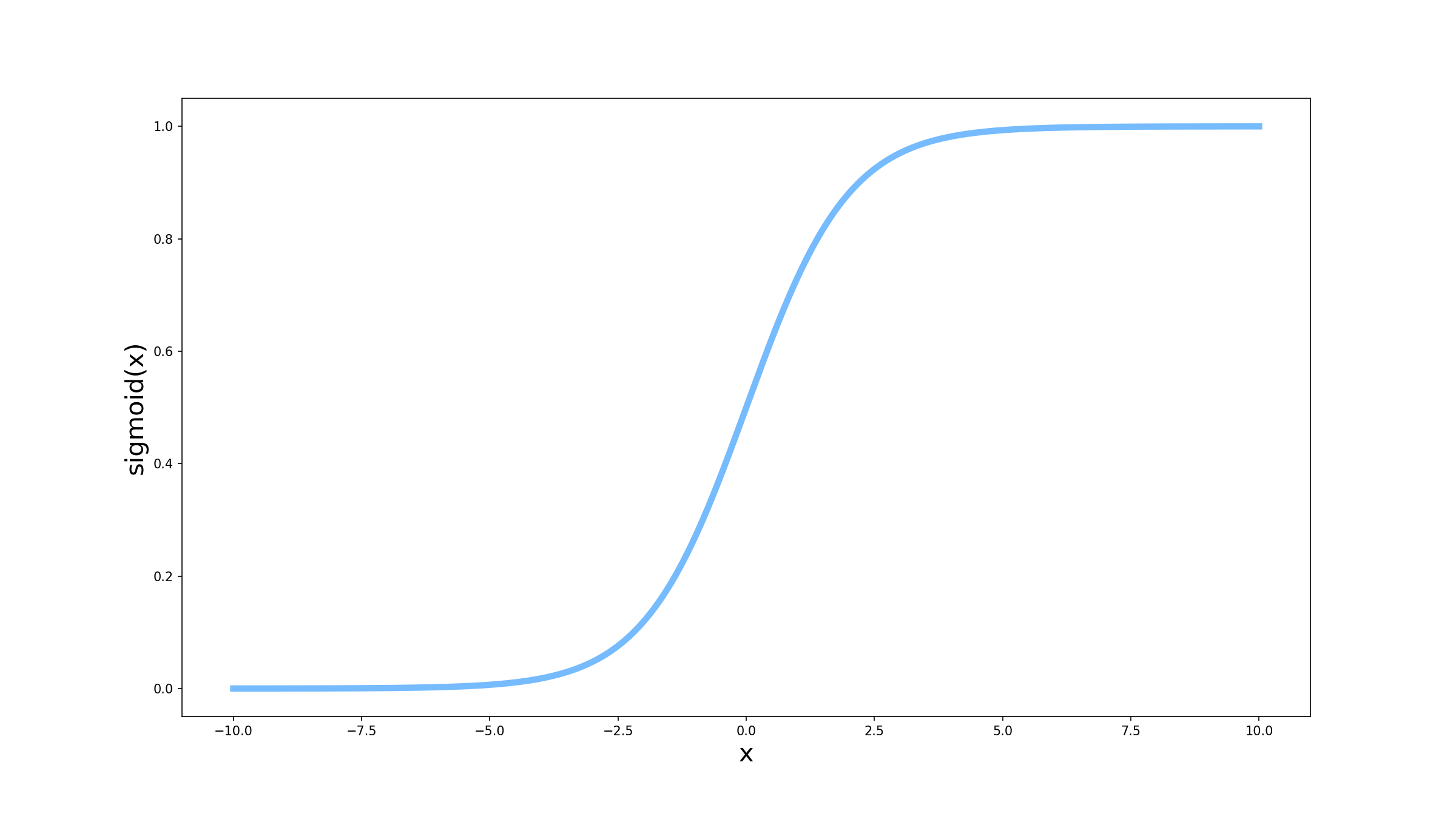
Se você disse que é porque ela limita a saída entre 0 e 1, você acertou! A função sigmóide é muito utilizada em camadas finais da rede para problemas de classificação, justamente porque ela garante que a saída sempre será um valor entre 0 (classe negativa) e 1 (classe positiva). Mas você pode se perguntar, por que não apenas colocar um limitante em 0 e em 1 como na função abaixo (vamos nos referir a ela como clip)?
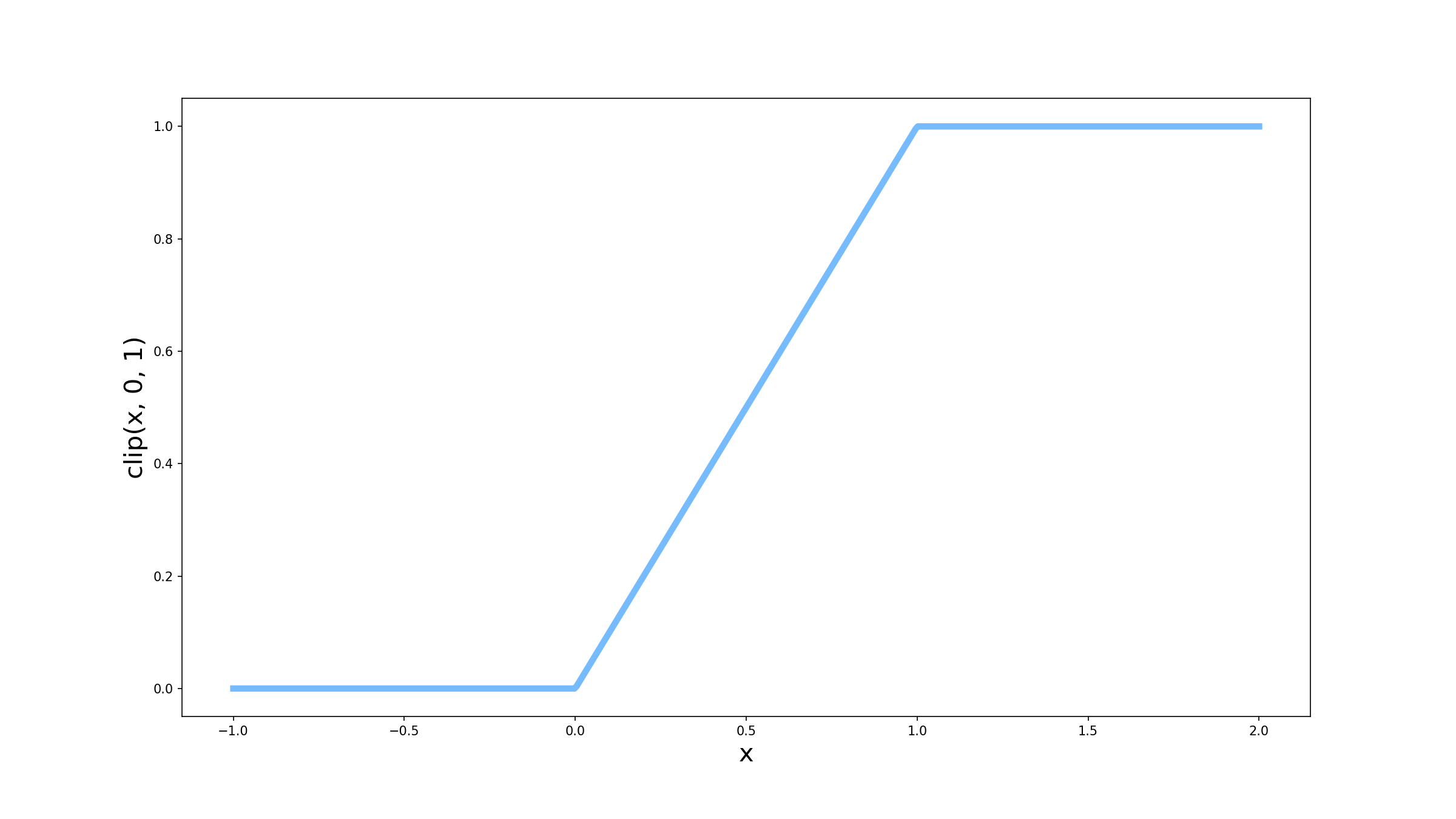
Para responder essa pergunta, temos que que voltar desta vez ao segundo artigo desta série (você pode dar uma conferida aqui). Nós havíamos encontrado uma equação para o cálculo do gradiente descendente que tinha a seguinte forma:
\[\frac{\partial \mathscr{L}}{\partial w} = \frac{\partial \mathscr{L}}{\partial ŷ}f^\prime(z) x, onde\] \[ŷ = f(z)\] \[z = w*x + b\]Podemos ver então que o gradiente da função de custo depende da derivada da função de ativação. Portanto, para escolher uma função de ativação, também temos que analisar como a derivada dela se comporta para entendermos melhor como o erro será propagado pela rede.
Vamos comparar então as duas funções que mostramos até agora, começando pela função clip. Um importante conceito que temos que relembrar para tornar nossa análise mais intuitiva é que a derivada de uma função escalar (que recebe um único número e retorna um único número) pode ser interpretada como a inclinação da curva em determinado ponto. Dessa forma, quando z for menor que 0 ou maior que 1, a derivada será igual a 0, pois as curvas são retas na horizontal. Já entre 0 e 1 a função tem a forma $f(z) = z$, e podemos concluir que a inclinação da curva é 1. Matematicamente, podemos escrever
\[f^\prime(z) = \begin{cases} 1 & \textrm{se } 0 \leq z \leq 1, \\ 0 & \textrm{c.c.} \end{cases}\]Perceba que a função clip possui dois “bicos”, em 0 e 1, o que significaria que a derivada não existe nesses pontos. Porém, para conseguirmos utilizar essa função, vamos assumir que em ambos os pontos, a derivada é igual a 1. Visualmente, temos o seguinte gráfico:
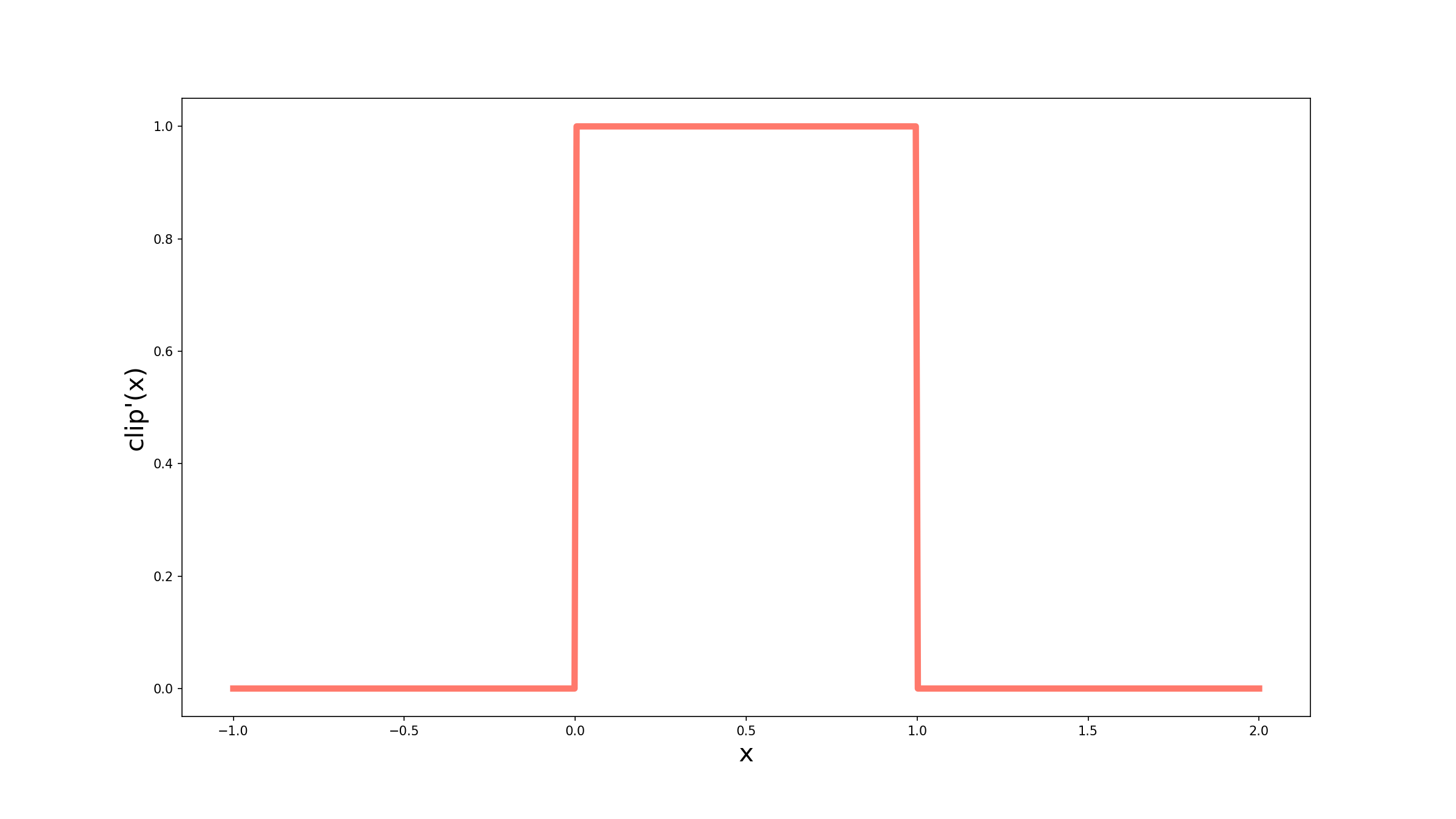
O grande problema dessa função é que se a saída da minha combinação linear for maior que 1 ou menor que 0 (o que é possível de acontecer dado o erro que a rede pode apresentar), $f^\prime(z) = 0$, o que implica $\frac{\partial \mathscr{L}}{\partial w} = 0$. Tá … mas na prática, por que isso importa pra mim? Porque quando esse gradiente vai para 0, o erro referente a essa amostra não vai ser utilizado para atualizar o peso, e muito provavelmente vamos continuar errando.
Isso não parece muito promissor, não é mesmo? Vamos olhar então a derivada da sigmóide. Aqui vamos recorrer a uma abordagem menos geométrica para encontrar a derivada. Vamos utilizar então a regra do quociente (a demonstração está escondida para não tornar o texto muito denso):
Demonstração - Derivada Sigmóide
$$\frac{d \sigma(x)}{dx} = \frac{d\frac{1}{dx} \times 1+e^{-x} - 1 \times \frac{d 1+e^{-x}}{dx}}{(1+e^{-x})^2}$$ $$\frac{d \sigma(x)}{dx} = \frac{e^{-x}}{(1+e^{-x})^2}$$ $$\frac{d \sigma(x)}{dx} = \frac{1}{1+e^{-x}} (\frac{\color{red}{1-1}+e^{-x}}{1+e^{-x}})$$ $$\frac{d \sigma(x)}{dx} = \sigma(x) (\frac{\color{red}{1}+e^{-x}}{1+e^{-x}} + \frac{\color{red}{-1}}{1+e^{-x}})$$E voilá! Temos nossa equação para a derivada da sigmóide. Vamos olhar agora como ela se comporta graficamente:
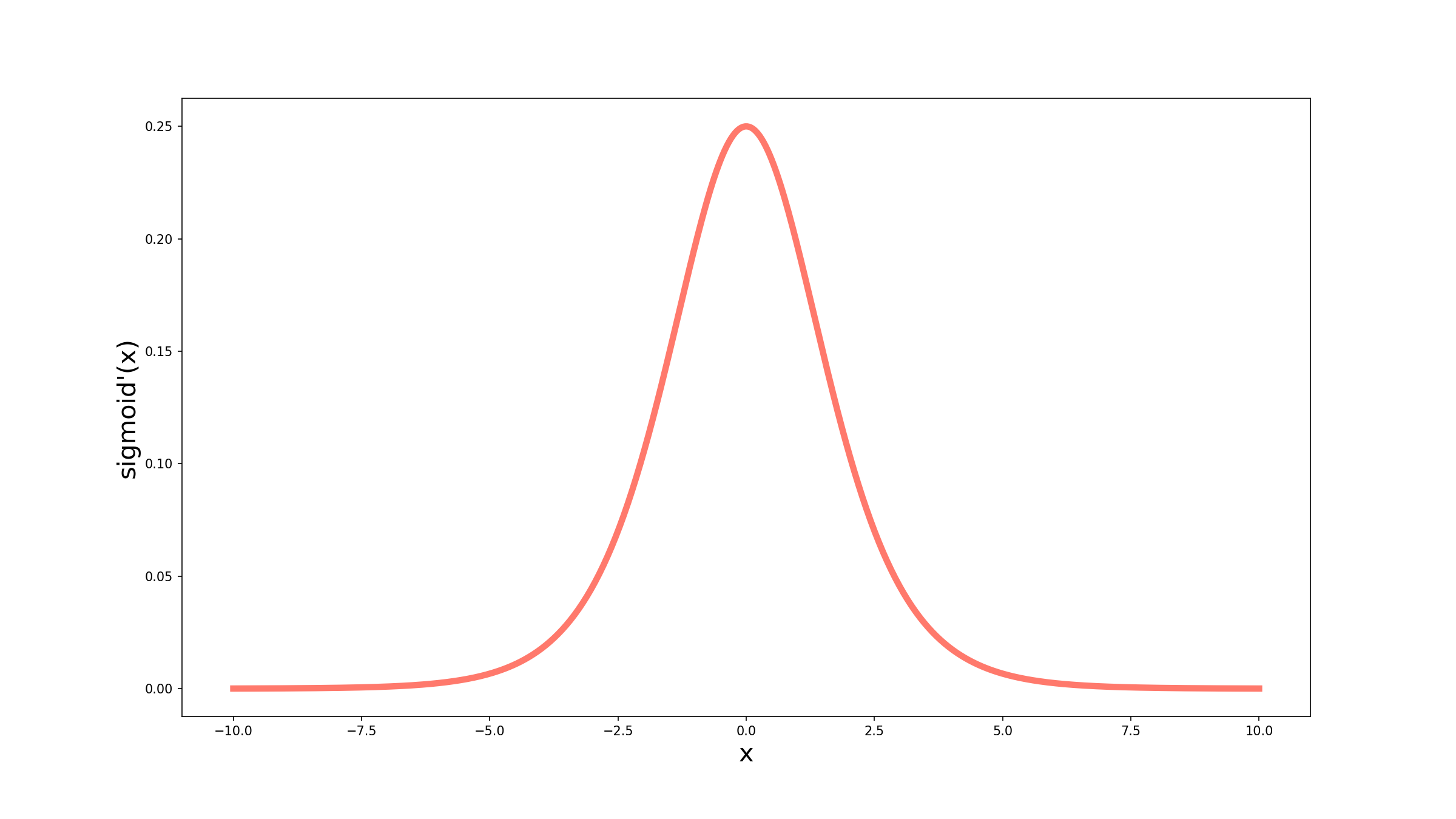
Comparando as duas curvas, podemos perceber que ambas, em algum momento, chegam a 0. A diferença entre elas está em como elas chegam e em quais valores de $x$. A derivada da sigmóide tem uma forma muito mais suave, e o que eu quero dizer com isso é que ela vai chegando a 0 aos poucos, enquanto a derivada da função clip tem uma mudança abrupta de 1 para 0. Além disso, no gráfico acima podemos observar que mesmo quando $x=-5$, por exemplo, a derivada da sigmóide não é zero. Isso nos auxilia na propagação do gradiente para as outras camadas da rede.
Tangente Hiperbólica
\[\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]Vamos tratar agora de outra função de ativação muito comum, chamada tangente hiperbólica. Mas por que vamos querer utilizar outra função que não a sigmóide se já vimos que ela atende todas as nossas necessidades? A explicação é que a sigmóide é muito boa na camada final da rede, muito pela restrição da saída entre 0 e 1. Mas no interior da rede essa propriedade não é importante e existem outras funções que nos ajudam a propagar o gradiente de forma mais eficiente, uma delas sendo a tangente hiperbólica. Vamos dar uma olhada em como ela se comporta.
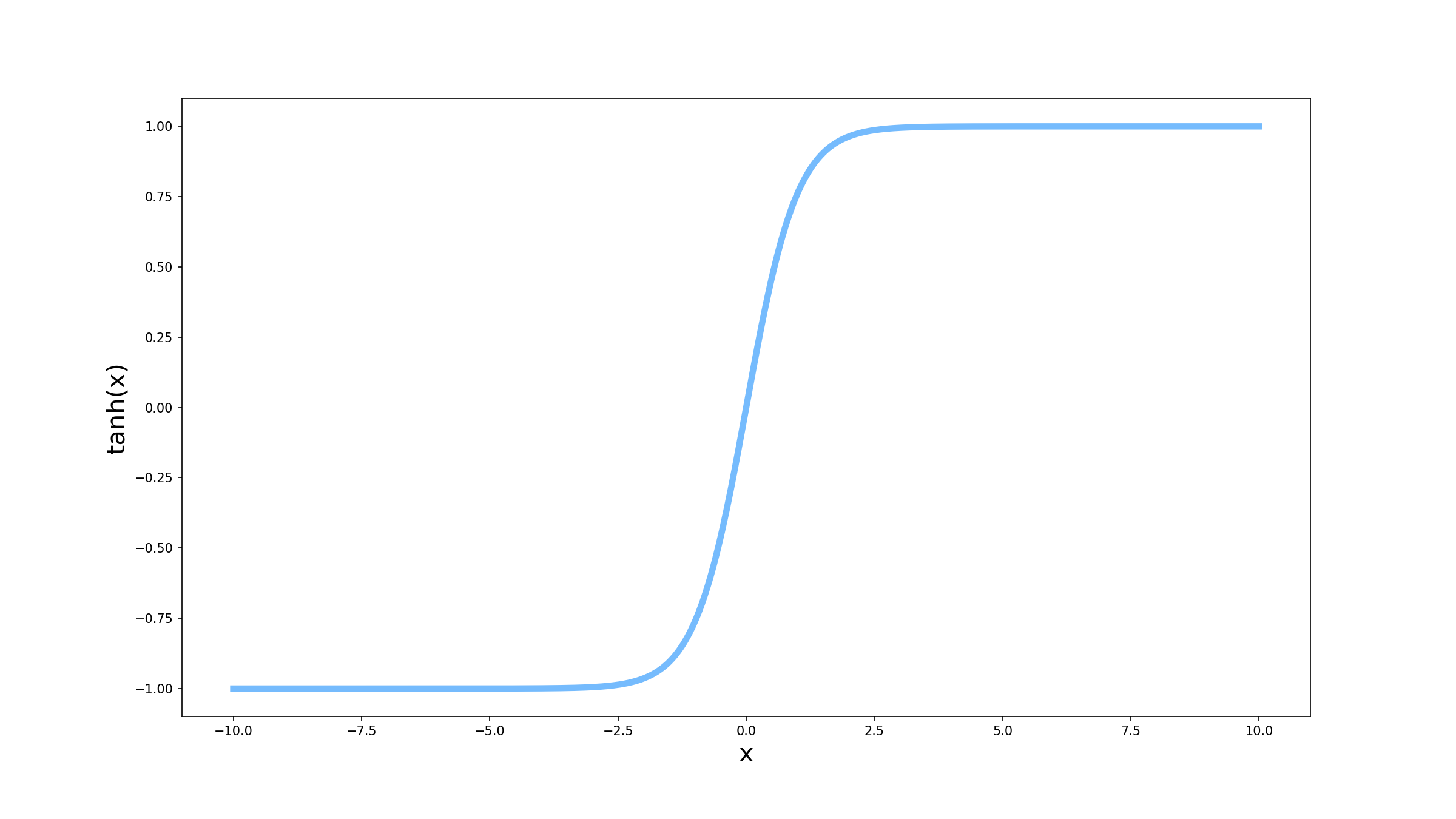
Pelo gráfico acima, a tangente hiperbólica tem uma forma muito parecida com a sigmóide. A principal diferença entre as duas é que a tangente hiperbólica tem valor mínimo -1, em vez de 0. Mas como isso ajudaria na propagação dos erros? Lembra que comentamos que a derivada pode ser vista como a inclinação da curva? O que acontece é que a tangente hiperbólica sai de -1 para chegar até 1 em um intervalo menor do que a sigmóide sai de 0 para chegar a 1. Isso significa que a inclinação da tangente hiperbólica tende a ser maior do que a da sigmóide, facilitando a atualização dos pesos.
Vamos encontrar a expressão da derivada da tangente hiperbólica primeiro e em seguida vamos comparar as duas curvas para vermos mais claramente a diferença entre elas. Aqui vamos seguir a mesma lógica de cálculo da derivada da sigmóide, utilizando a regra do quociente (novamente vamos omitir a demonstração mas, para quem quiser, é só clicar no botão):
Demonstração - Derivada Tangente Hiperbólica
$$\frac{d \tanh(x)}{dx} = \frac{\frac{d e^{x} - e^{-x}}{dx} \times (e^{x} + e^{-x}) - (e^{x} - e^{-x}) \times \frac{de^{x} + e^{-x}}{dx}}{(e^{x} + e^{-x})^2}$$ $$\frac{d \tanh(x)}{dx} = \frac{(e^{x} + e^{-x}) \times (e^{x} + e^{-x}) - (e^{x} - e^{-x}) \times (e^{x} - e^{-x})}{(e^{x} + e^{-x})^2}$$ $$\frac{d \tanh(x)}{dx} = \frac{(e^{x} + e^{-x})^2 - (e^{x} - e^{-x})^2}{(e^{x} + e^{-x})^2}$$ $$\frac{d \tanh(x)}{dx} = \frac{(e^{x} + e^{-x})^2}{(e^{x} + e^{-x})^2} - \frac{(e^{x} - e^{-x})^2}{(e^{x} + e^{-x})^2}$$Ótimo! Agora que já temos a nossa expressão, vamos plotar o gráfico das duas derivadas juntas.
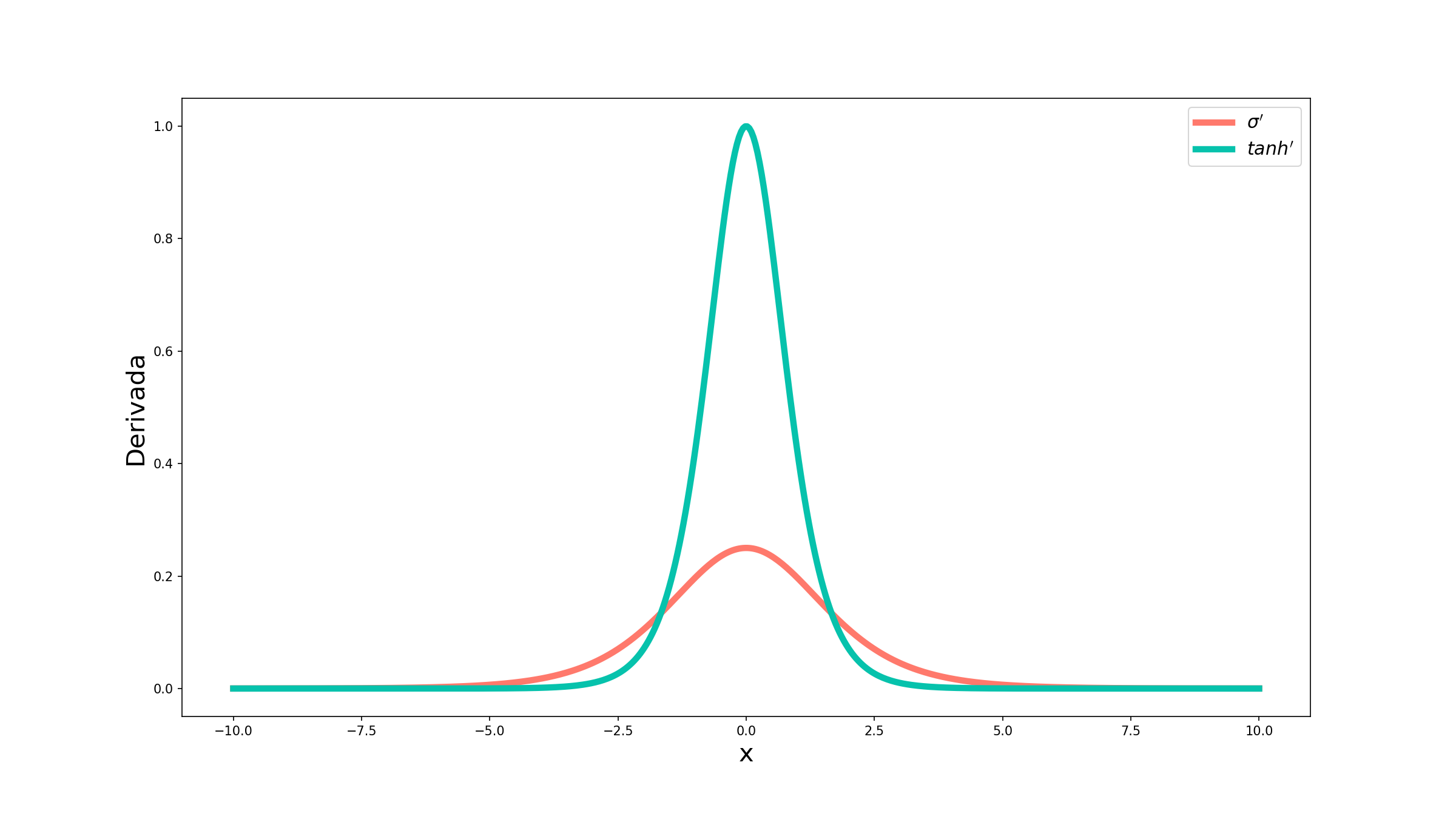
Agora sim podemos ter uma boa visão de como as derivadas sem comportam de forma diferente. Embora a derivada da tangente hiperbólica (curva em verde) vá para 0 mais rapidamente que a derivada da sigmóide (curva em vermelho/laranja), o valor dela entre -1 e 1 supera, e muito, o valor da sigmóide. Dessa forma, fica claro que os erros são melhor propagados pela tangente hiperbólica.
ReLU
\[ReLU(x) = max(0, x)\]Chegamos agora à última função que vamos abordar nesse artigo, a chamada ReLU (do inglês, Rectfied Linear Unit). O comportamento da ReLU é bastante curioso quando a comparamos com as outras funções vistas até agora: ela é basicamente a própria combinação linear quando ela é maior ou igual à 0, e é sempre 0 quando a combinação linear é menor que 0.
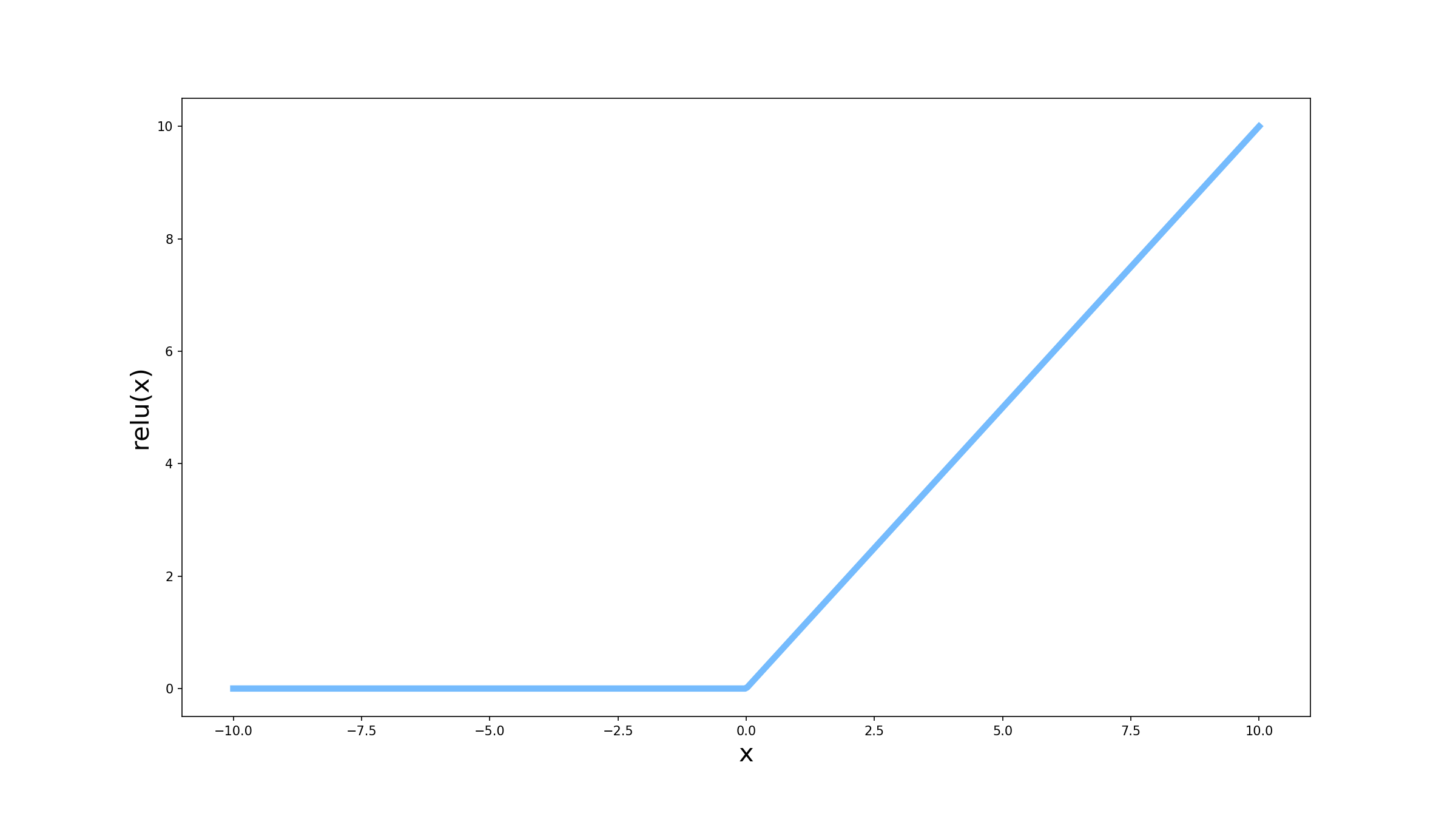
Mas qual a vantagem de utilizar essa função em vez de alguma outra que já vimos? E sendo ela uma função basicamente linear não cairíamos no mesmo problema de não ter função de ativação?
Vamos começar pela segunda pergunta: não, não teremos esse problema. Apesar de a ReLU parecer linear, o fato de que limitamos em 0 faz com que ela não seja. Isso é suficiente para garantir que temos então uma função de ativação que funciona. Para verificar a primeira questão vamos analisar o gráfico da derivada da ReLU. Seguindo o mesmo raciocínio de como calculamos a derivada da função clip, a expressão para a derivada da ReLU é:
\[ReLU^\prime(x) = \begin{cases} 1 & \textrm{se } x \lt 0, \\ 0 & \textrm{c.c.} \end{cases}\]Graficamente então temos:
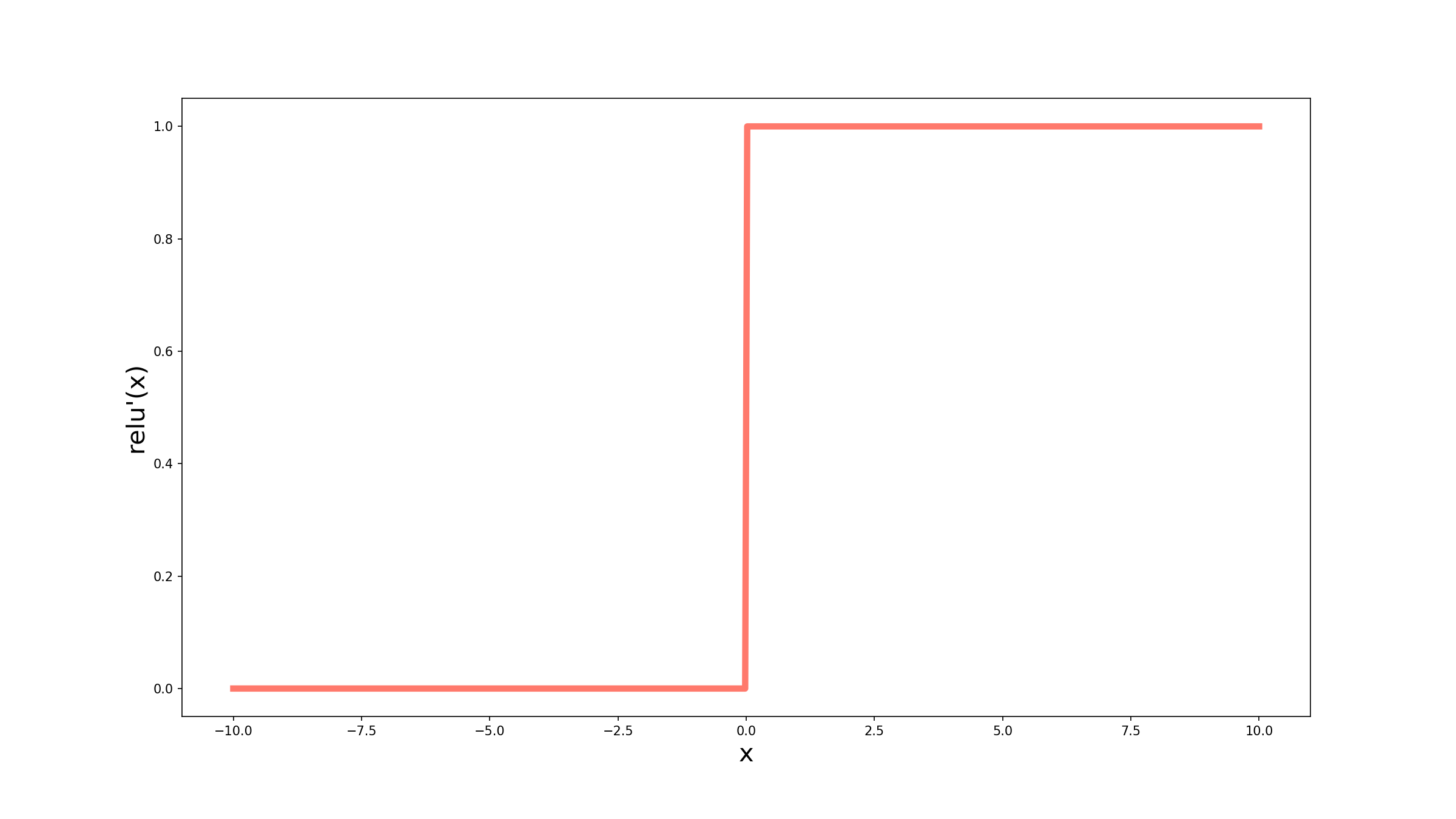
Podemos ver que qualquer valor menor ou igual que 0 tem derivada igual a 0, ou seja, o erro não é propagado. Mas quando analisamos os valores acima de 0, vemos que a derivada é sempre igual a 1. A derivada da tangente hiperbólica também tinha um valor de pico em 1, mas era um valor pontual, conforme íamos para a direita ou para a esquerda esse valor ia diminuindo.
Dissipação do gradiente
Até agora, falamos muito que era interessante que as derivadas das funções de ativação fossem mais altas porque isso ajudava a propagar o erro pela rede, mas qual a intuição por trás disso? Lembre-se que o segredo por trás do gradiente descendente é a regra de cadeia aplicada em cada camada da rede. Isso significa que a expressão do gradiente para determinada camada é a multiplicação do gradiente de todas as camadas superiores a ela com as derivadas relativas àquela camada. Dessa forma, fazendo algumas simplificações de notação, podemos escrever para uma rede de 2 camadas:
\[\frac{\partial \mathscr{L}}{\partial w_1} = f_2^\prime(z_2)f_1^\prime(z_1) U,\]em que $U$ são os outros termos da equação que não as derivadas das funções de ativação. Se tivessemos 3 camadas:
\[\frac{\partial \mathscr{L}}{\partial w_1} = f_3^\prime(z_3)f_2^\prime(z_2)f_1^\prime(z_1) U\]Podemos ver então que a cada nova camada, um novo termo é adicionado. Mas o que acontece se esses termos forem muito pequenos (entre 0 e 1)? Bom quanto mais termos pequenos, menor será o resultado da multiplicação. Isso significa que as camadas mais próximas da entrada da rede possuem um gradiente muito pequeno, fazendo que com os pesos sejam atualizados de maneira muito leve ou nem sejam atualizados! Esse problema é conhecido como dissipação do gradiente (do inglês, vanishing gradient). Vamos fazer uma simulação bem simples para fixar a ideia.
Suponha que tenhamos uma rede com 10 camadas, e que (por um sinal do destino) todas as combinações lineares dessas camadas dêem como resultado 0,5. Vamos simular 3 redes, uma com cada função de ativação que vimos. Gráfico abaixo mostra como o termo com as multiplicações das derivadas das funções de ativação (que aqui chamamos de $M$) se comporta em cada uma das camadas.
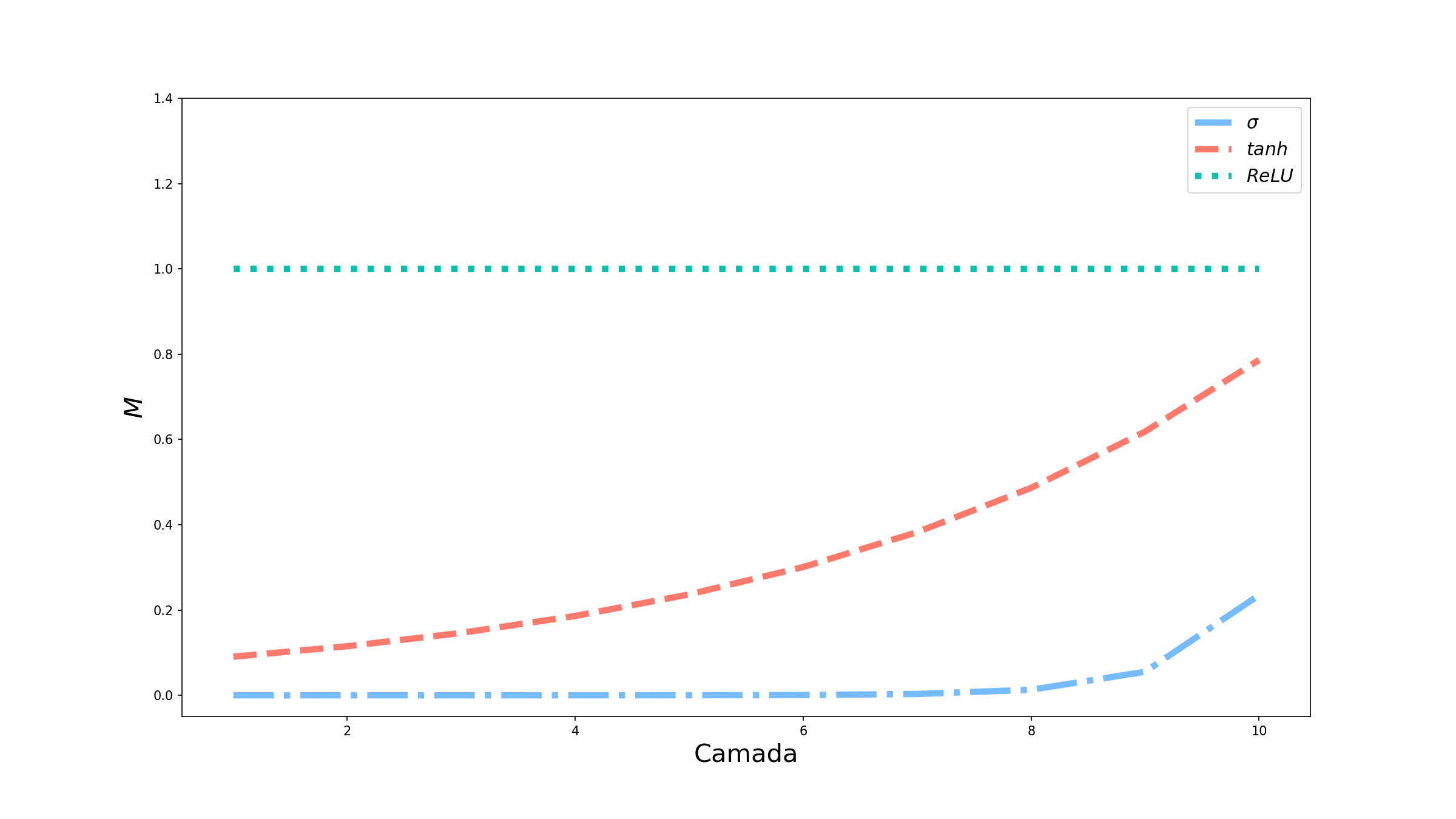
A curva da sigmóide cai rapidamente para 0, indicando que todas as camadas abaixo da camada 7/8 não terão seus pesos atualizados. Já a tangente hiperbólica possui um comportamento melhor, sendo que em 10 camadas ela ainda não convergiu para zero. Por esse motivo, ela é mais utilizada nas camadas intermediárias do que a sigmóide. Mas conforme aumentamos o número de camadas, a tendência é que ela também vá para 0. Finalmente, a ReLU apresenta um comportamento totalmente constante: independente da camada $M=1$, o que facilita a propagação do erro em camadas menos profundas.
Conclusão
Hoje falamos sobre a importância das funções de ativação, mostramos alguns exemplos muito utilizados e as características que as fazem serem escolhidas em diversos contextos. Entretanto, esses foram só alguns exemplos. Existem diversas funções de ativação que podem ser melhores dependendo do tipo de problema (por exemplo, softmax, leaky-relu, gelu, etc.). Também comentamos sobre o problema de dissipação do gradiente, mas existe o problema oposto: explosão do gradiente (do inglês, exploding gradient), em que a multiplicação leva a valores muito grandes. Todos esses são problemas que valem ser explorados, caso tenham interesse.
E agora?
Esse foi o último artigo dessa primeira série sobre redes neurais. Ainda pretendo escrever mais sobre outros tipos de redes, como as redes recorrentes, redes convolucionais e transformers, mas elas serão escritas em séries separadas. Também pretendo falar sobre outros algoritmos de aprendizado de máquina em séries futuras. Espero que tenham gostado do conteúdo desses primeiro artigos e fiquem ligados: em breve teremos novos conteúdos para vocês!

