10 min de leitura
Distâncias

Distâncias
Fala, pessoal! No último post apresentamos as ideias de viés e variância. Falamos um pouco também sobre como esses conceitos podem ser vistos no modelo dos K vizinhos mais próximos. Se você ainda não leu, corre lá que a gente te espera! Hoje vamos falar sobre outro conceito muito utilizado em diversos algoritmos de aprendizado de máquina e, de novo, vamos recorrer ao KNN (do inglês, K Nearest Neighbors) para nos auxiliar nessa explicação.
Será que eles são parecidos?
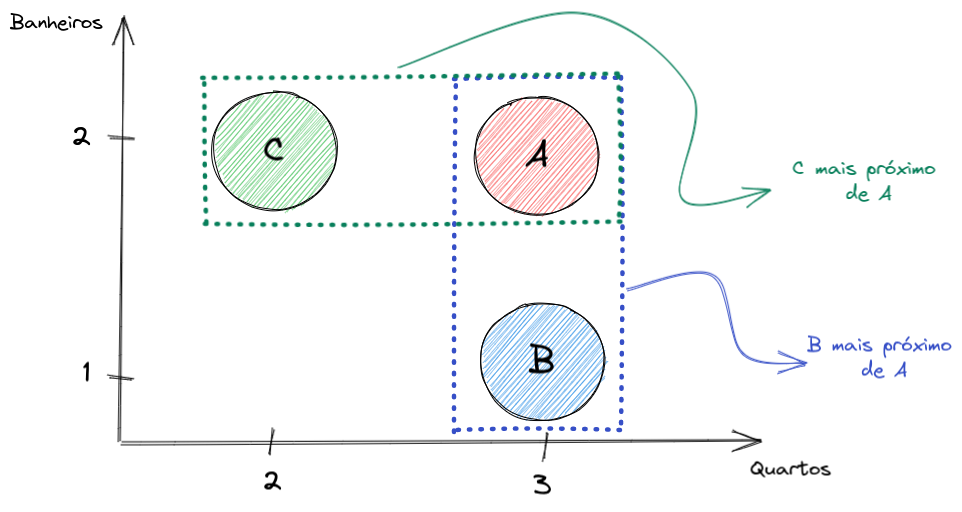
A base do KNN é encontrar pontos que são parecidos (os famosos vizinhos). Talvez você ainda não tenha parado para se questionar, mas o que faz um ponto ser parecido com outro? Vamos voltar ao nosso exemplo de previsão do preço de casas: eu posso considerar que duas casas são parecidas se elas tiverem um número semelhante de quartos. Por exemplo, se a casa A e a casa B têm 3 quartos e outra casa C tem apenas 2 quartos, podemos dizer que a casa B é mais próxima da casa A do que a casa C. Nossa, parece muito simples não é mesmo? Agora vamos supor que queremos incluir outras informações como o número de banheiros na casa. As casas A, B e C têm, respectivamente, 2, 1 e 2 banheiros. Pelo número de banheiros, a casa mais parecida com a casa A é a casa C. Hmmm … agora complicou um pouco. E se quiséssemos considerar as duas informações ao mesmo tempo? Parece complicado, mas não é (talvez só um pouco). Mas antes de dar mais detalhes, vamos definir formalmente o que é uma função de distância.
Uma definição formal (até demais)
Matematicamente, uma função de distância pode ser definida da seguinte forma:
Uma distância d sobre um conjunto $\mathbb{X}$ é uma função $d:\mathbb{X}\ \times\ \mathbb{X} \to [0, \infty)$
E, para todo $x,y,z \in \ \mathbb{X}$, satisfaz:
- $d(x,y) = 0 \iff x = y$
- $d(x,y) = d(y,x)$
- $d(x,y) \leq d(x,z) + d(z,y)$
As funções de distância também podem ser chamadas de métricas. Eu particularmente acho a notação matemática um pouco intimidadora ao primeiro contato. Para facilitar um pouco o entendimento, vamos quebrar a definição em algumas partes.
Comecemos com:
\[d:\mathbb{X}\ \times\ \mathbb{X} \to [0, \infty)\]Essa talvez seja a parte mais complicada, mas vamos lá: primeiramente, d é uma função, o que significa que ela recebe alguma informação como entrada e devolve outra informação na saída. “Mas o que raios é uma informação?”, você corretamente deve ter se perguntado. No caso da entrada, a função d recebe uma dupla (ou seja, dois pontos) que pertencem ao conjunto $\mathbb{X}$. Mas isso ainda não quer dizer muita coisa, afinal o que é esse conjunto $\mathbb{X}$. Na realidade, ele pode ser qualquer coisa: se estamos falando da distância entre 2 números reais então $\mathbb{X}$ é $\mathbb{R}$; se estamos falando da distância entre vetores de duas dimensões (por exemplo, latitude e longitude), $\mathbb{X}$ é $\mathbb{R}^2$; se estamos tentando calcular a distância entre duas palavras, então $\mathbb{X}$ é o conjunto de todas as palavras possíveis. Agora que falamos sobre o que é uma informação na entrada da função, vamos ver qual informação a função d nos retorna. Pela definição, os valores dessa função podem assumir qualquer valor entre 0 e infinito e aqui já temos uma restrição importante: as distâncias nunca podem ser negativas.
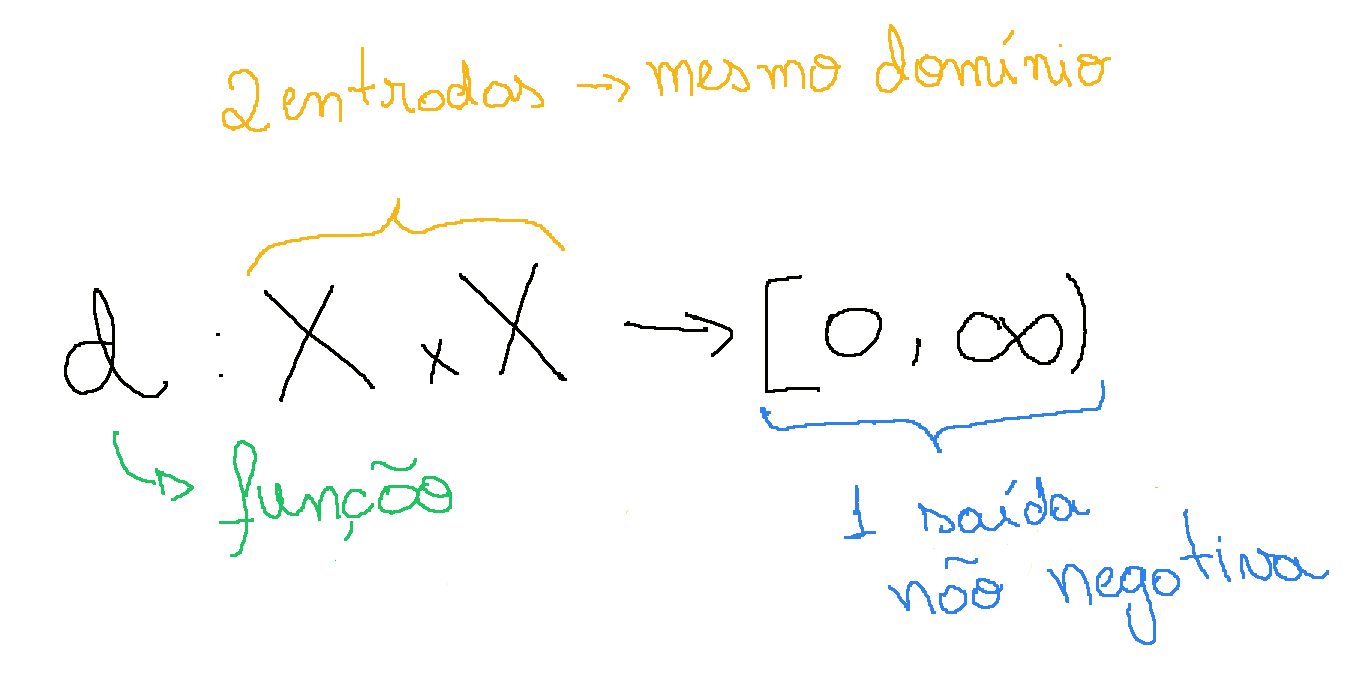
Partimos agora para entender o que significam as propriedades listadas acima. Para todas elas vamos pensar no exemplo de localização de casas.
- A propriedade 1 quer dizer que duas casas só terão distância 0 entre elas, se, e somente se, elas forem a mesma casa. Pense por exemplo no seu vizinho: por mais próximas que suas casas sejam, você ainda precisa dar alguns passos para sair da sua casa e chegar na dele;
- A propriedade 2 diz que a distância entre a sua casa e a casa do seu vizinho é a mesma distância entre a casa do seu vizinho e a sua, ou seja, não importa a ordem em que mostramos os pontos, a distância é a mesma;
- A propriedade 3 implica que se você quiser ir à casa de um amigo, o menor caminho é ir direto pra lá. Se você, por exemplo, passar para visitar um segundo amigo, a soma da distância entre a sua casa e a do segundo amigo com a distância entre a casa dos dois amigos, é, no mínimo, igual à distância entre a sua casa e a casa do primeiro amigo.
Alguns exemplos comuns de distâncias
Agora que já definimos o que é uma distância, vamos dar alguns exemplos de funções famosas.
Euclidiana
A distância mais comumente utilizada é chamada distância euclidiana, também conhecida como L2. Ela é definida, para o caso de $n$ dimensões, pela equação abaixo:
\[\text{Euclidiana}(x,y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}\]Ela parece bem complicada, né. Vamos analisar um caso em duas dimensões para simplificar. Suponha que tenhamos dois pontos $x=(0;0)$ e $y=(2;2)$. A distância euclidiana entre x e y é dada por:
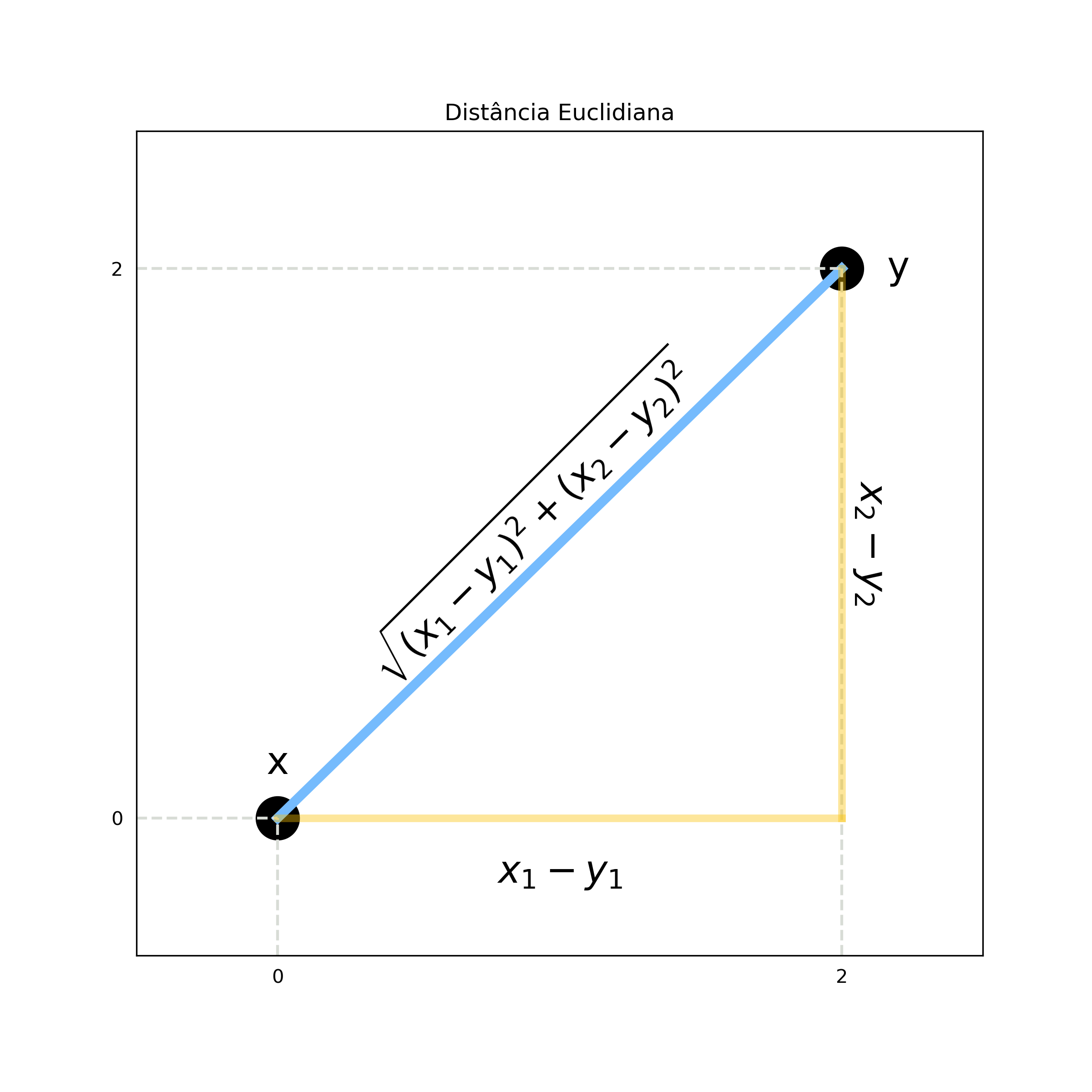
\[\text{Euclidiana}(x,y) = \sqrt{(x_1-y_1)^2 + (x_2-y_2)^2} =\] \[\sqrt{(0-2)^2 + (0-2)^2} = \sqrt{4+4} = \sqrt{8} = 2,83\]Se você acha que já viu essa equação em algum lugar, você muito provavelmente está se lembrando do Teorema de Pitágoras. Como a imagem abaixo mostra, a distância euclidiana nada mais é (no caso de 2 dimensões) o valor do comprimento da hipotenusa.
Manhattan
A distância de Manhattan, ou L1, é muito similar à distância euclidiana. A diferença entre as duas é que, em vez de elevarmos ao quadrado o valor das diferenças, agora pegamos apenas os valores absolutos e não temos que tirar a raiz quadrada. Para $n$ dimensões, essa métrica é definida por:
\[\text{Manhattan}(x,y) = \sum_{i=1}^n |x_i - y_i|\]Utilizando o mesmo exemplo anterior, temos:
\[\text{Manhattan}(x,y) =\] \[|x_1-y_1| + |x_2-y_2| = |0-2|+ |0-2| = 2 + 2 = 4\]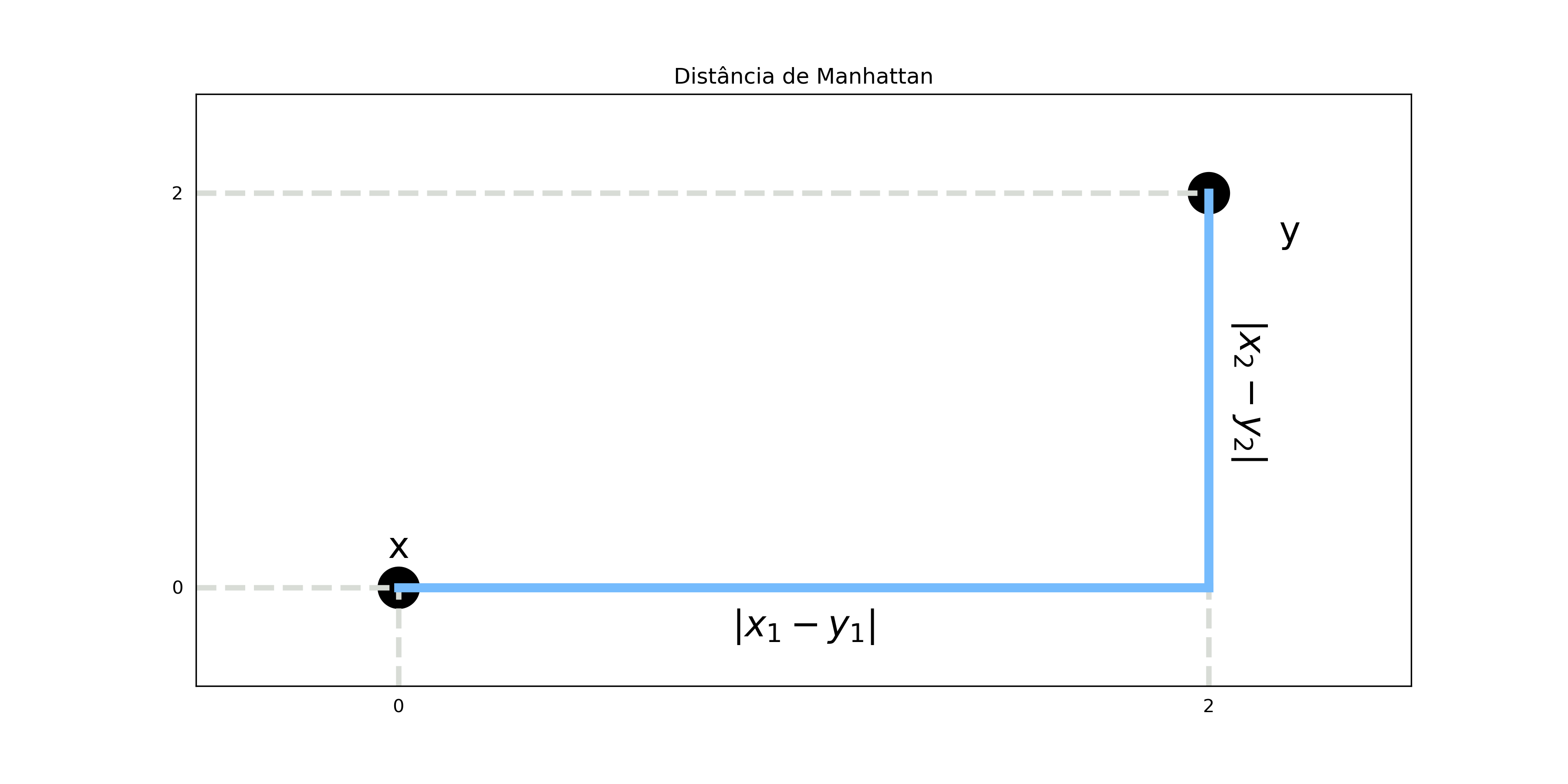
Um leitor curioso deve estar com a pulga atrás da orelha para saber porque o nome dessa distância é Manhattan. Esses leitores não precisam ficar aflitos pois, além de muito conteúdo de ciência de dados, também trazemos várias curiosidades. A razão pela qual essa distância tem esse nome é que ela nos dá a quantidade de passos unitários perpendiculares a um dos eixos que temos que dar para chegar de um ponto a outro, como se estivéssemos andando pelos quarteirões de um cidade (Manhattan, no caso).
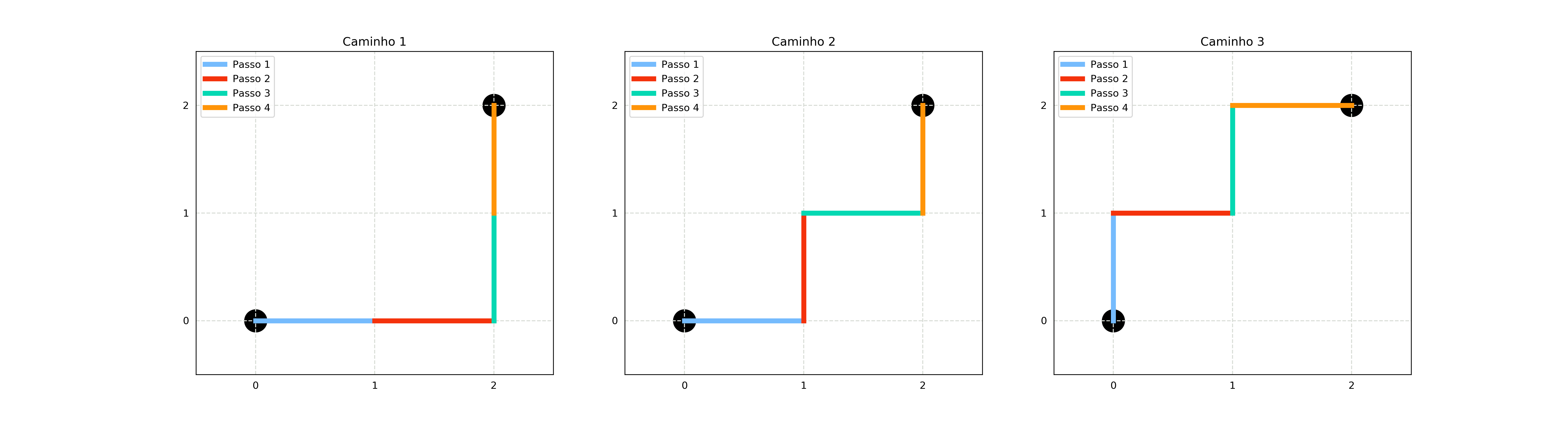
Minkowski
Na realidade, tanto a distância euclidiana quanto a distância de Manhattan fazem parte de uma família mais genérica de distâncias chamada Minkowski. A formulação dessa métrica é a seguinte, para uma ordem $p$ qualquer:
\[\text{Minkowski}(x,y) = \sqrt[\leftroot{7}\uproot{5}p]{\sum_{i=1}^n |x_i - y_i|^p}\]Podemos observar que para $p=2$ temos a distância euclidiana e para $p=1$ temos a distância de Manhattan.
Só por questão de curiosidade vamos observar como a métrica se comporta no exemplo anterior quando alteramos $p$.
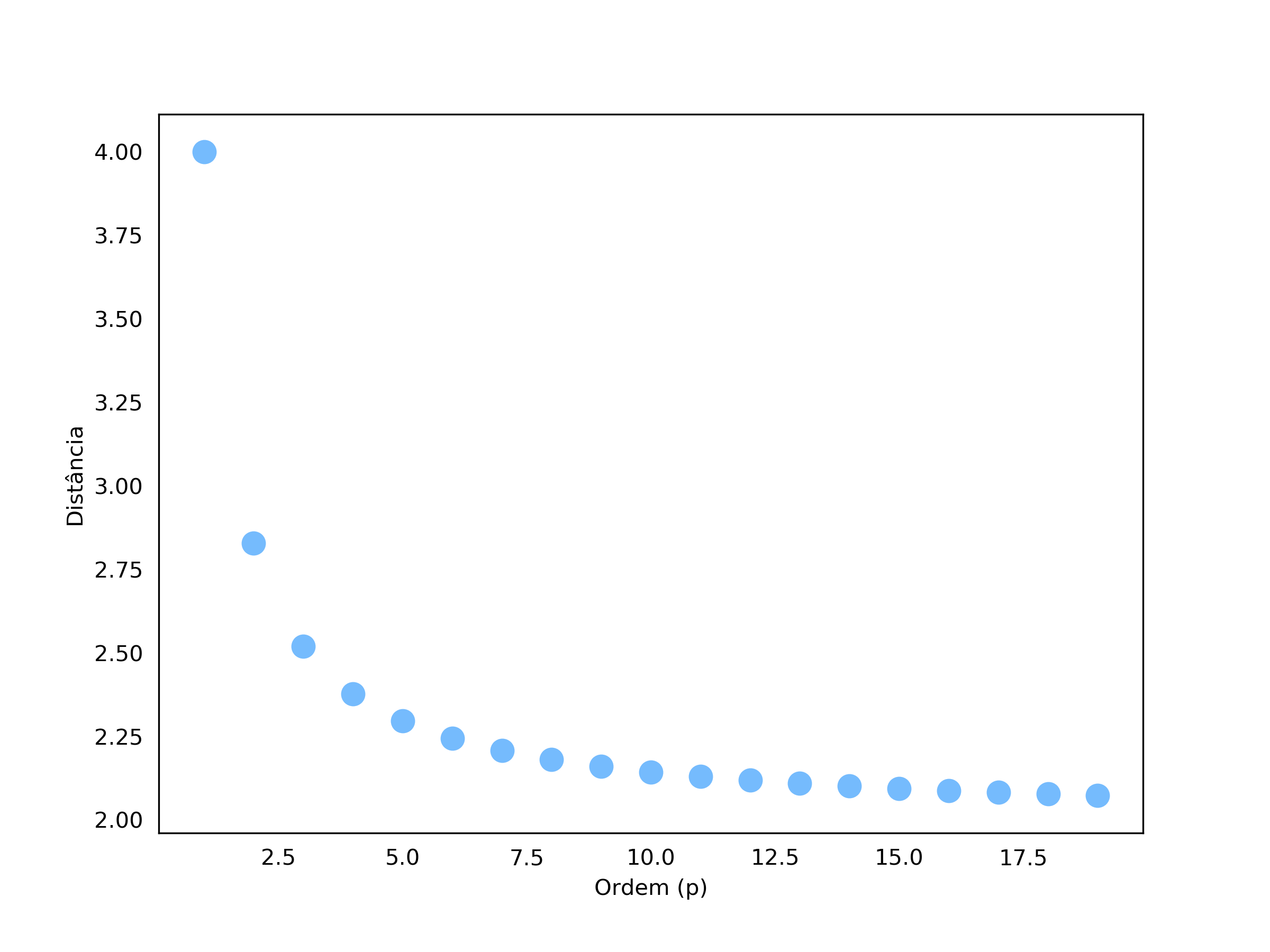
Podemos ver que conforme aumentamos a ordem, a curva parece convergir para 2. Na realidade, quando $p = \infty$, o valor da distância de Minkowski converge para a distância da dimensão com distância individual (que nesse caso é realmente 2), ou seja:
\[\lim_{p\to\infty} \text{Minkowski}(x,y) = \max(|x_1-y_1|, |x_2-y_2|, ..., |x_n-y_n|)\]Esse limite também é conhecido como distância de Chebyshev.
Menção honrosa - “Distância” do cosseno
Existem inúmeras outras distâncias como a distância de Hamming, a distância de Jaccard, etc. Cada uma dessas métricas tem uma aplicação diferente e pode ser útil em diferentes contextos. Mas antes de finalizar, gostaria de analisar uma última “distância” muito famosa por sua utilização no processamento de texto: a distância do cosseno.
Matematicamente, ela é definida como:
\[\text{DistCosseno}(x,y) = 1 - \text{SimCosseno}(x,y)\] \[\text{SimCosseno}(x,y) = \frac{x \bullet y}{\sqrt{x \bullet x}\sqrt{y \bullet y}},\]onde $\bullet$ indica o produto interno. A similaridade do cosseno (SimCosseno) indica qual o cosseno entre o ângulo formado pelo vetor $x$ e o vetor $y$. Quanto maior o ângulo entre eles, menos alinhados estão os dois vetores e menor a similaridade. Por consequência, quanto menor a similaridade maior é a distância entre os vetores. Desse modo, a distância do cosseno mede o quão alinhados dois vetores estão.
Na verdade, a distância do cosseno não satisfaz a propriedade 1, ou seja, dois vetores, mesmo que diferentes podem ter distância 0 entre si caso estejam perfeitamente alinhados. Por esse motivo, em alguns momentos eu escrevi “distância” entre aspas. Mesmo assim, devido a sua grande aplicação prática vamos estudá-la aqui.
Mas quando vamos querer utilizar essa medida em vez de alguma outra?
A distância do cosseno é muito utilizada quando a magnitude dos vetores não importa. Um exemplo prático é em análise de textos. Suponha que tenhamos 3 textos (A, B e C). Vamos considerar como variáveis a quantidade de vezes que a palavra “Esporte” aparece e a quantidade de vezes que a palavra “Livros” aparece.
Os dados são os seguintes:
| Texto | Esporte | Livros |
|---|---|---|
| A | 1 | 2 |
| B | 3 | 1 |
| C | 3 | 4 |
Calculando a distância euclidiana entre A e B temos
\[\text{Euclidiana}(A,B) = 2,23\]Já entre A e C temos
\[\text{Euclidiana}(A,C) = 2,83\]Baseando-nos nessa análise, poderíamos concluir que o texto A é mais parecido com B do que com C. Mas antes de fazermos qualquer afirmação, vamos analisar os vetores graficamente.
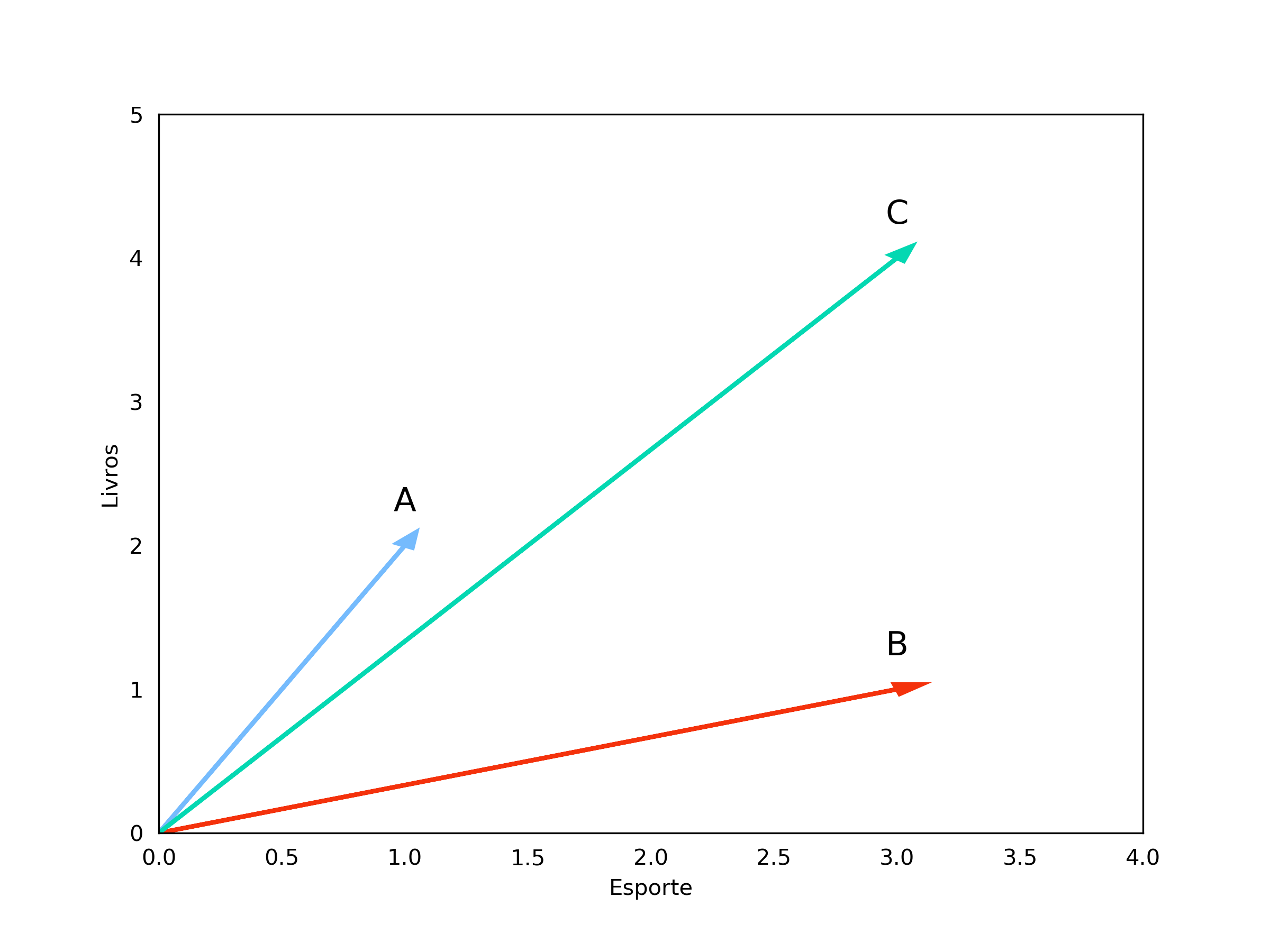
Podemos observar que a orientação do vetor C é muito mais próxima de A do que a orientação do vetor B, ou seja, a proporção entre o número de ocorrências de “Livros” e “Esporte” é mais parecida entre os textos A e C do que entre A e B. Nós podemos interpretar essa orientação, como o assunto do texto. Por exemplo, os textos A e C parecem falar sobre livros de esporte, enquanto o texto B parece ser mais focado em esportes no geral.
Mas então porque a distância euclidiana diz que o texto C é menos parecido com o texto A? Se considerarmos que os textos podem ter tamanhos diferentes, a diferença entre A e C pode ser dada por C ser mais longo, uma vez que só estamos contando cada vez que uma palavra ocorre.
Vamos analisar agora a distância do cosseno entre os vetores. Comecemos com alguns cálculos auxiliares para os vetores A e B:
\[A \bullet B = 1*3 + 2*1 = 5\] \[\sqrt{A \bullet A} = \sqrt{1*1 + 2*2} = \sqrt{5}\] \[\sqrt{B \bullet B} = \sqrt{3*3 + 1*1} = \sqrt{10}\]Colocando esses valores nas fórmulas da distância do cosseno, temos:
\[\text{SimCosseno}(A, B) = \frac{5}{\sqrt{5}*\sqrt{10}} = 0,71\]e, consequentemente,
\[\text{DistCosseno}(A,B) = 1 - \text{SimCosseno} = 0,29\]Fazendo o mesmo processo para os vetores A e C, temos a seguinte distância:
\[\text{DistCosseno}(A,C) = 0,02\]Por essa métrica, agora A e C são mais próximos que A e B. De maneira geral,se estivermos mais interessados na diferença de orientação dos vetores, a utilização da distância do cosseno é indicada.
Conclusão
Chegamos ao fim de mais um artigo e dessa vez pudemos aprender um pouco mais sobre distâncias: o que são, como calculá-las e alguns exemplos. Lembrando que existem inúmeras funções que podem ser utilizadas e cada problema pode ter uma função mais adequada. Aqui só cobrimos alguns exemplos. Se você gostou da explicação, por favor compartilhe para que mais pessoas possam aprender também! Até a próxima!

