9 min de leitura
Tipos de gradiente descendente
Fala, pessoal! No último artigo discutimos um pouco sobre como fazemos para as redes neurais aprenderem com o algoritmo do Gradiente descendente. Durante a explicação nós vimos dois cenários: para tornar o exemplo mais tangível, nós calculamos o gradiente baseado no erro de predicação de um única amostra, mas depois comentamos que o ideal é utilizar mais de uma amostra para realizar o treino porque isso deixava o algoritmo mais estável. Hoje vamos analisar mais a fundo o que isso significa e ter uma intuição melhor de como utilizar o algoritmo.
Cenário
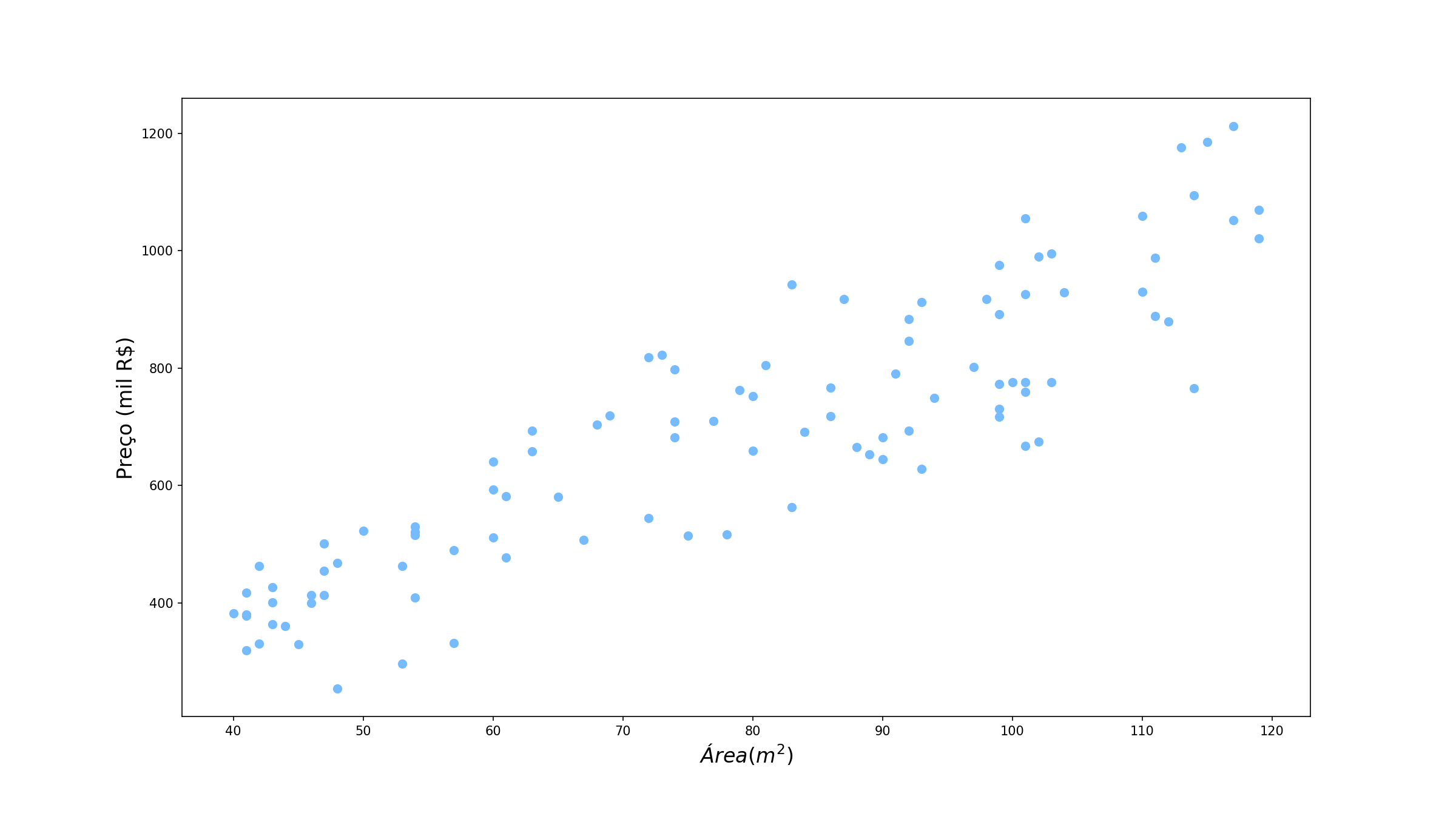
Nos últimos artigos nós estavamos trabalhando com um problema de predição do peso de uma pessoa com base na altura dela. Hoje vamos estudar um caso um pouco diferente: vamos tentar prever o preço de um imóvel, com base na área dele. Perceba que ainda estamos com um problema de regressão nas mãos (estamos tentando prever uma variável contínua, o preço do imóvel) com uma única variável. O que é apenas qual é essa variável e qual a variável explicativa que estamos utilizando. Vamos dar uma olhada nos nossos dados:
Para efeitos didáticos, vamos continuar utilizando a rede neural que tinhamos antes: uma rede com uma única camada e um único neurônio, com função de ativação identidade.
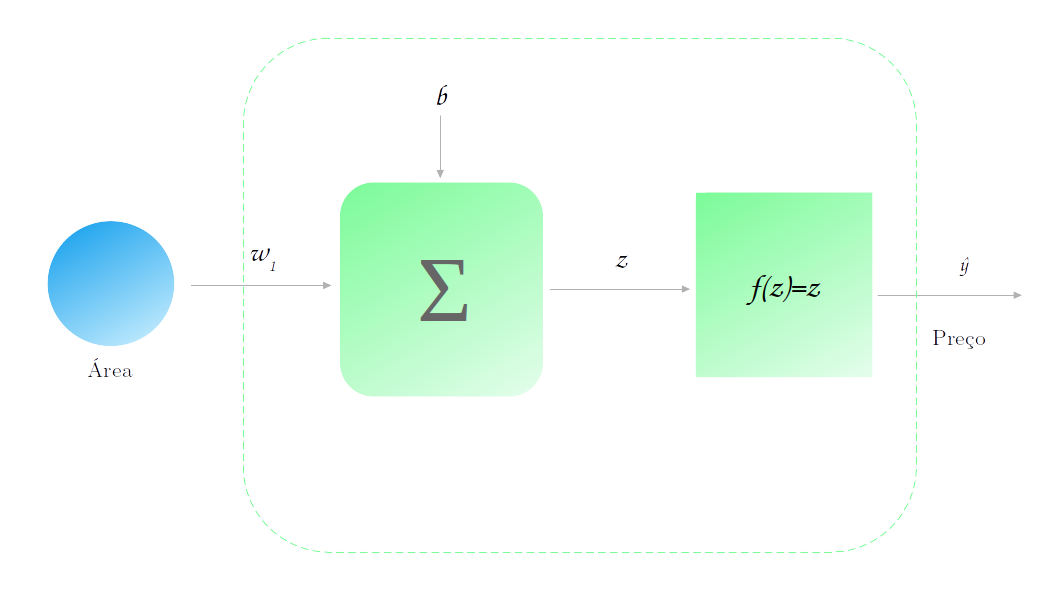
Ou seja, a nossa função de modelagem do problema é da forma:
\[\mathcal{Preço} = \mathcal{Área}*w_1 + b\]Intuição
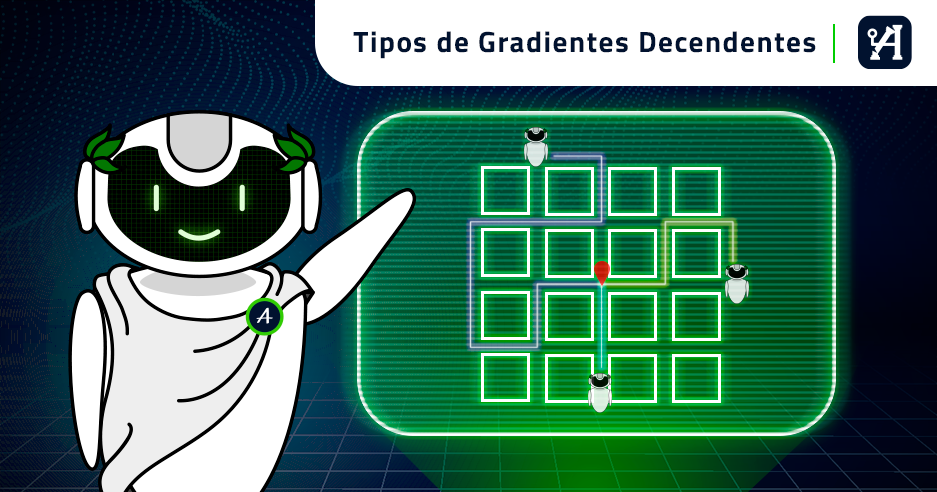
Antes de continuar com os gráficos e a matemática, vamos olhar um cenário completamente diferente que vai nos ajudar a entender um pouco problema que temos. Vamos supor que o nosso querido amigo Alex (finalmente nomeamos o nosso amigo!) está meio perdido na cidade. Ele precisa chegar no ponto indicado na imagem, mas não tem ideia de como.
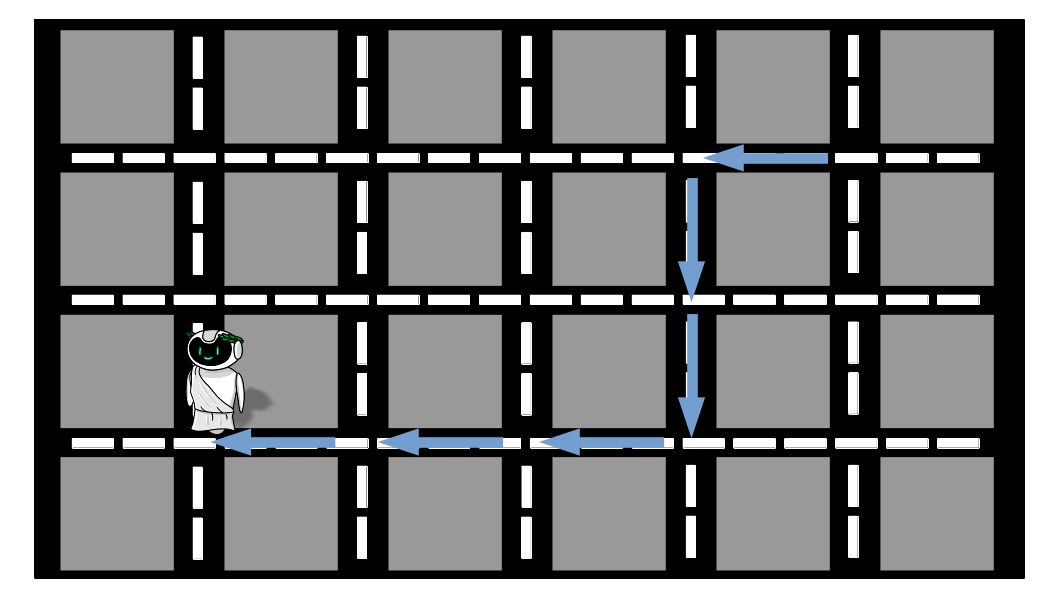
Inicialmente, ele decide seguir a estratégia de perguntar a uma pessoa por vez para onde ele deve ir. Além disso, nenhuma pessoa tem conhecimento total da cidade, elas dão a direção que acham estar correta, mas sem nenhuma garantia de que aquele é o melhor caminho mesmo. Ele também confia igualmente em todas as pessoas, embora elas pareçam confusas (o que acontece frequentemente) ou confiantes: se uma pessoa diz para ele seguir uma direção, ele segue, sempre andando um quarteirão por vez para ter certeza de que não passou do ponto (lembram-se de quando falamos da taxa de aprendizagem?). Vamos lá então, suponha que a primeira pessoa para quem ele pergunta diz que ele tem que andar para a esquerda. Nosso amigo anda então um quarteirão para a esquerda, e repete o processo.
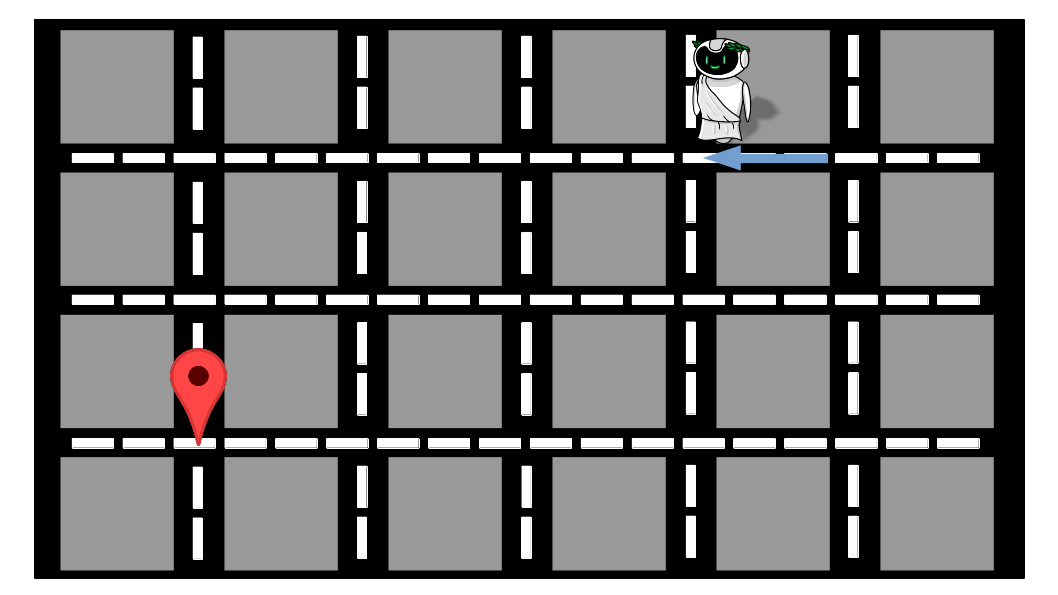
Vamos assumir que esse tenha sido o roteiro que o Alex seguiu, perguntando para cada pessoa:
- A segunda pessoa indica que ele deve descer;
- A terceira que ele deve ir para a direita;
- A quarta que ele deve descer;
- A quinta e a sexta que ele deve ir para a esquerda;
- A sétima que ele deve descer mais uma vez;
- A oitava e a nona que ele deve ir para a esquerda;
- Por fim, a décima diz que ele deve ir para cima.
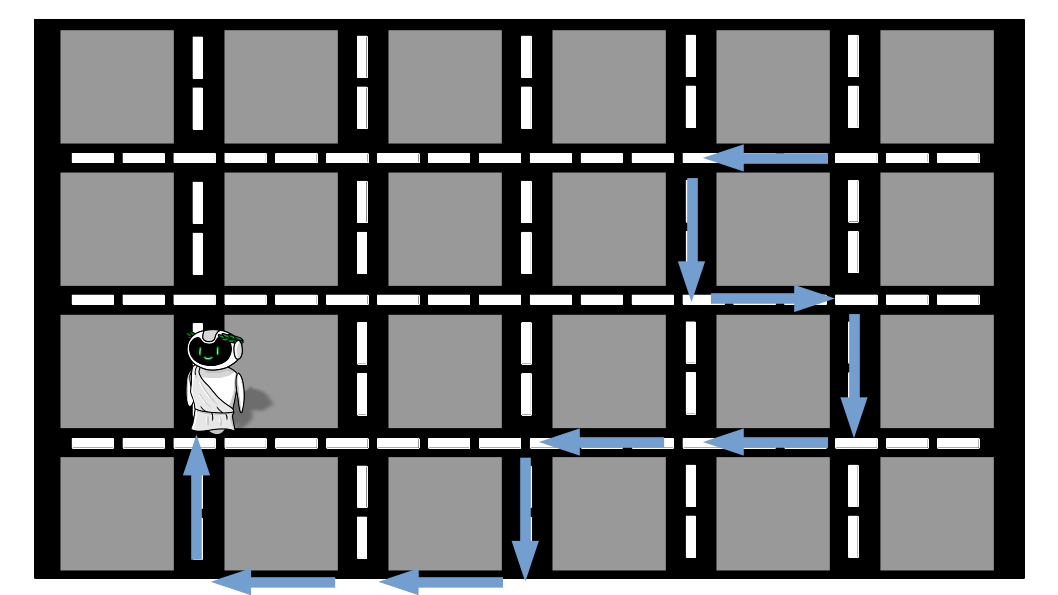
Ufa! Depois de muito andar e perguntar, Alex conseguiu chegar ao seu destino. Mas olhando atentamente ao trajeto percorrido, podemos perceber que existem trechos que são desnecessários e atrasaram nosso amigo (setas em vermelho). Isso acontece porque nenhuma das pessoas sozinha tem conhecimento da cidade inteira e, dessa forma, estão sujeitas a cometer erros.
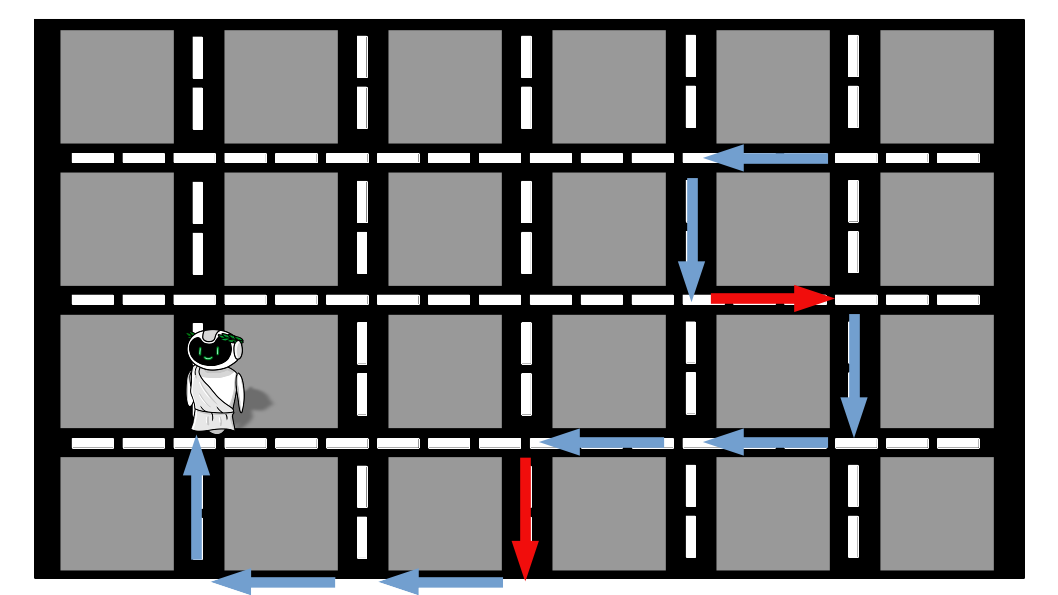
Como Alex é um cara muito curioso, ele se perguntou o que teria acontecido se ele tivesse perguntado para mais pessoas e tivesse considerado a opinião do conjunto para decidir para onde iria. No dia, seguinte ele decidiu fazer o teste: voltou ao mesmo local e agora iria tentar chegar no local desejado perguntando para um grupo de pessoas. Ele decidiu que 10 era um número adequado e que a direção que ele tomaria seria aquela que tivessido maior ocorrência entre as 10 recomendações. Sendo assim, ele só andaria na direção indicada quando tivesse atingido as 10 opiniões.
Abaixo podemos ver o que aconteceu:
- O primeiro grupo teve 8 pessoas dizendo esquerda e 2 dizendo para descer, logo ele foi para a esquerda;
- No segundo grupo, 4 pessoas disseram para ele ir para a esquerda e 6 para ele descer, então ele desceu;
- No terceiro grupo, 3 pessoas disseram para ele ir para a esquerda, 2 para ele ir para a direita e 5 para ele descer;
- No quarto, 8 disseram esquerda, 1 para cima e 1 para baixo;
- No quinto, 2 disseram para baixo, 2 para a direita e 6 para a esquerda;
- O sexto grupo teve as 10 pessoas dizendo para ele ir para a esquerda.
Oba! O Alex chegou ao destino sem ter percorrido nenhum trecho desnecessário, mesmo que algumas pessoas individualmente tivessem dado indicações incorretas. Mas ainda tinha algo incomodando Alex: mesmo que agora ele tivesse ido direto, ele havia demorado mais tempo do que no dia anterior. Quando ele parou para refletir ele percebeu que perguntar para 10 pessoas tomava tempo demais e era muito cansativo, apesar de que desse modo ele teria uma informação com maior probabilidade de estar correta. Ele então se perguntou:

E adivinhem o que ele fez? Isso mesmo! Voltou no dia seguinte para testar sua teoria. Agora ele desse decidiu que ia perguntar para apenas 5 pessoas. A imagem abaixo indica o trajeto percorrido naquele dia.
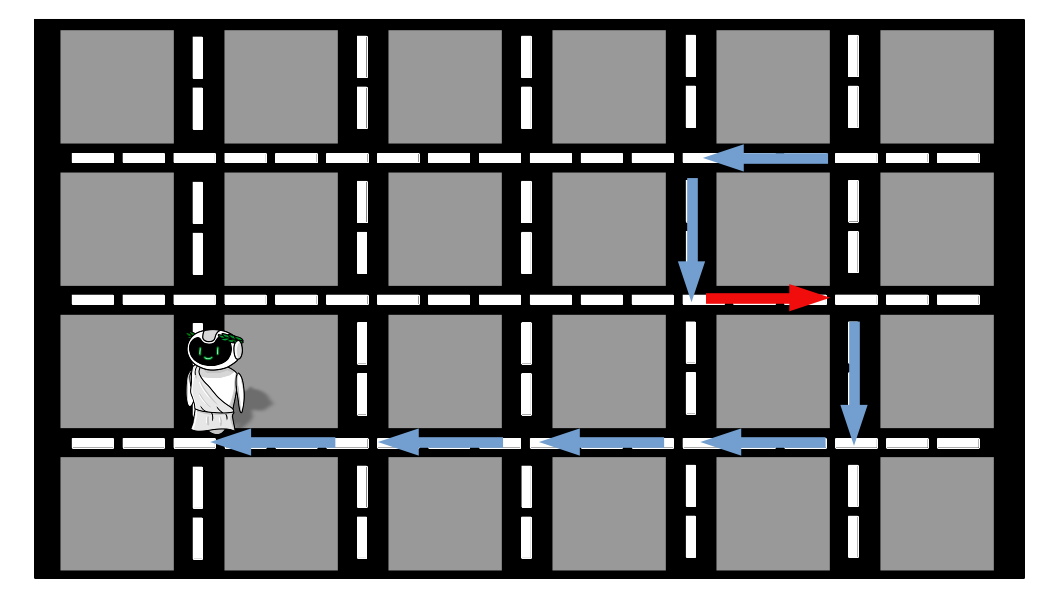
Podemos perceber duas coisas: primeiro que ainda tivemos um trecho que não era o ideal, mas foi apenas um e não dois como no primeiro dia. Segundo que o esforço e o tempo gasto em perguntar para 5 pessoas são muito menores do que perguntar para 10 pessoas. Assim, utilizando um valor intermediário nós balanceamos o custo entre ter muita incerteza e demorar muito tempo. Na verdade o tempo para chegar até o local desejado foi até menor do que perguntar para uma pessoa só, pois ele precisou fazer menos desvios desnecessários.
Voltando à rede
Vamos entender agora como a saga do Alex para chegar ao seu destino se relaciona com o número de exemplos que utilizamos para atualizar os pesos do modelo. Para isso, vamos fazer a seguinte suposição (somente para deixar a explicação mais compreensível): o valor do parâmetro $b$ do modelo vai ser iniciado em 0 e não vai ser atualizado nas iterações. Na prática, isso significa que agora nossa modelagem é dada por:
\[\mathcal{Preço} = \mathcal{Área}*w_1\]Agora, utilizando o nosso conjunto de dados, vamos ver como o erro quadrático médio (MSE do inglês Mean Squared Error) varia conforme variamos o valor de $w_1$.
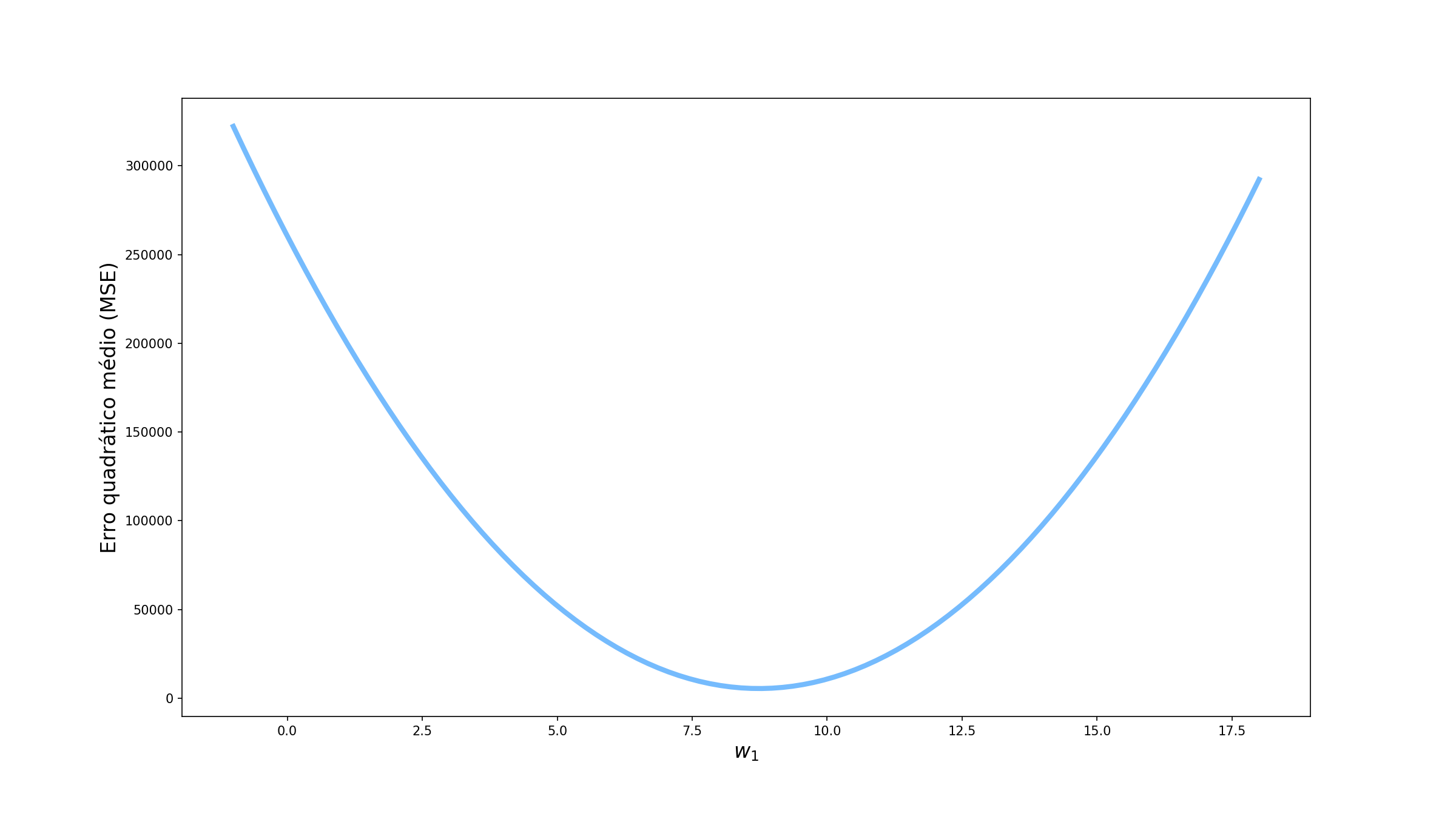
O ideia é que percorramos essa curva tentando encontrar o valor de $w_1$ que minimize o erro. Vamos tentar então as 3 abordagens que foram utilizadas pelo Alex:
Todos os pontos de uma vez
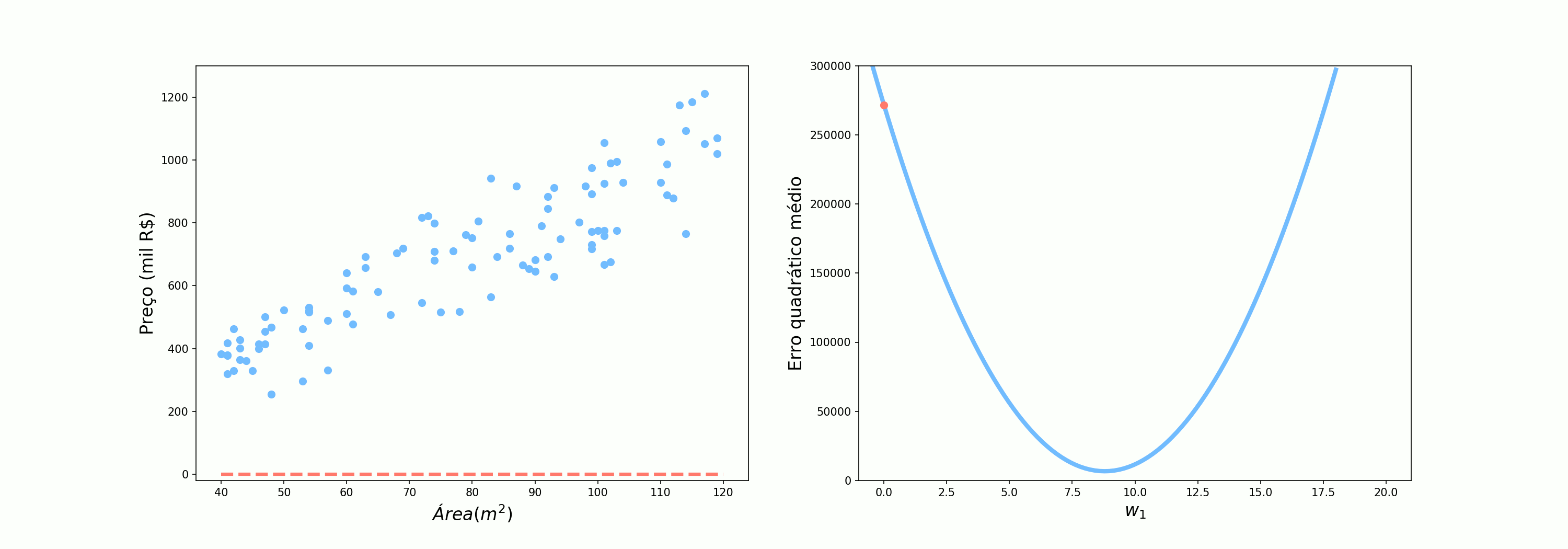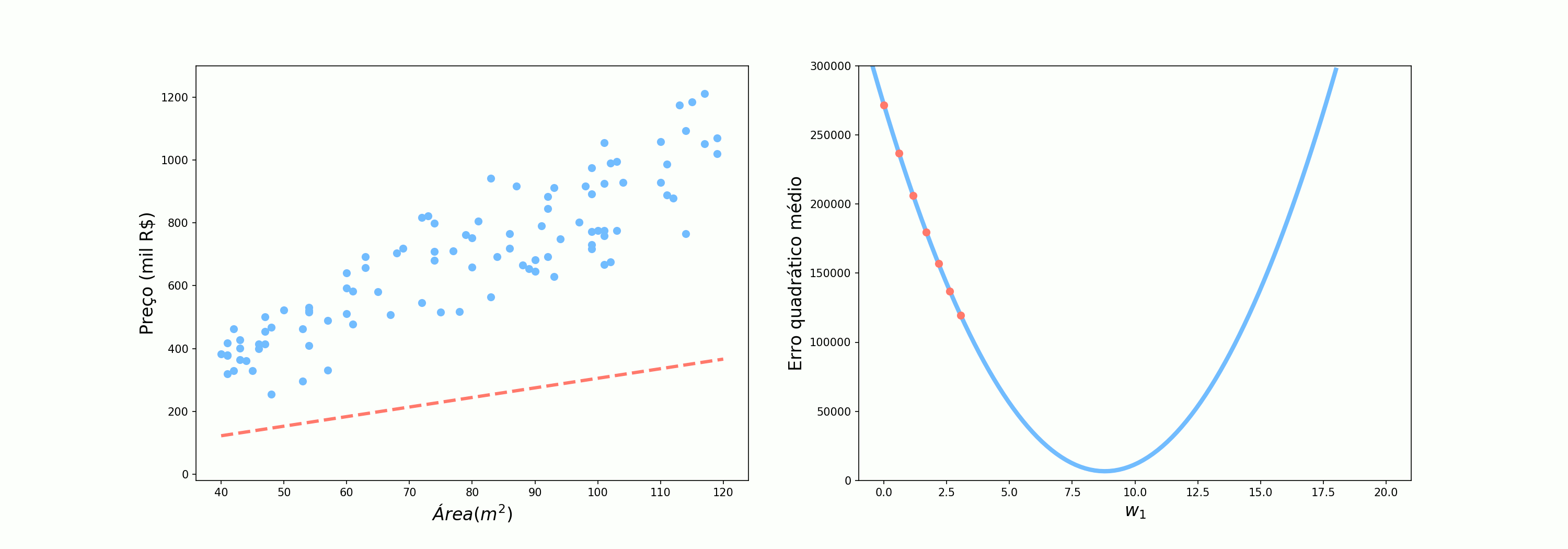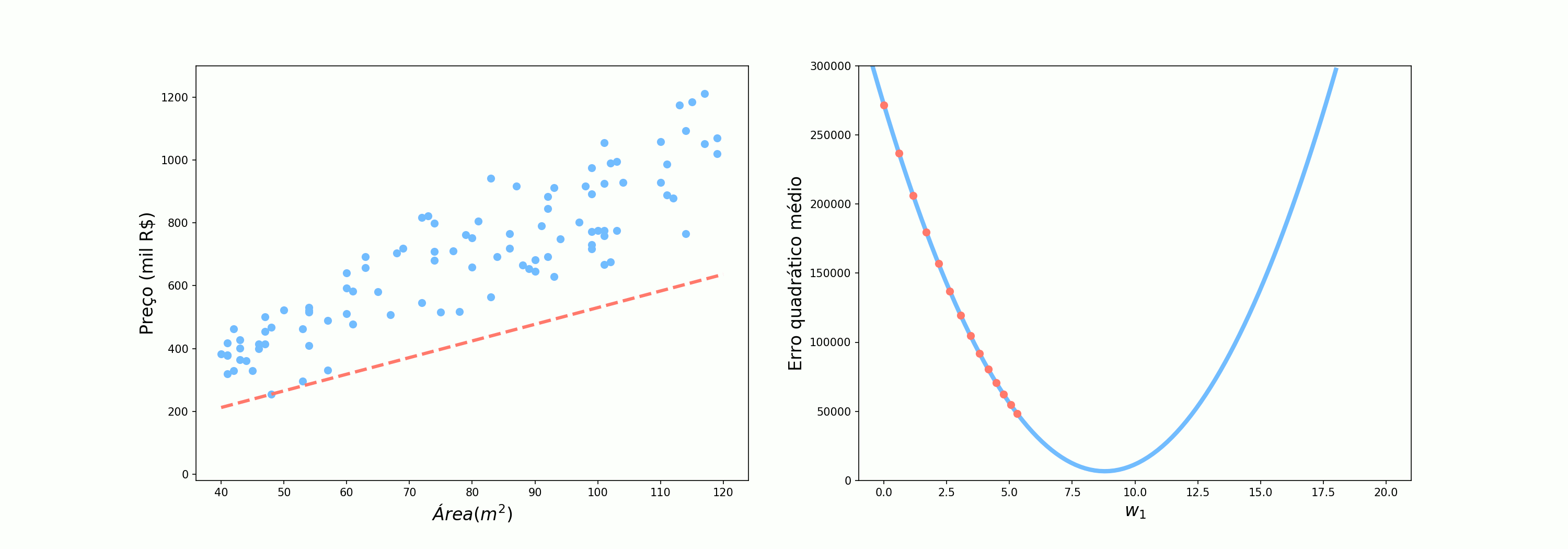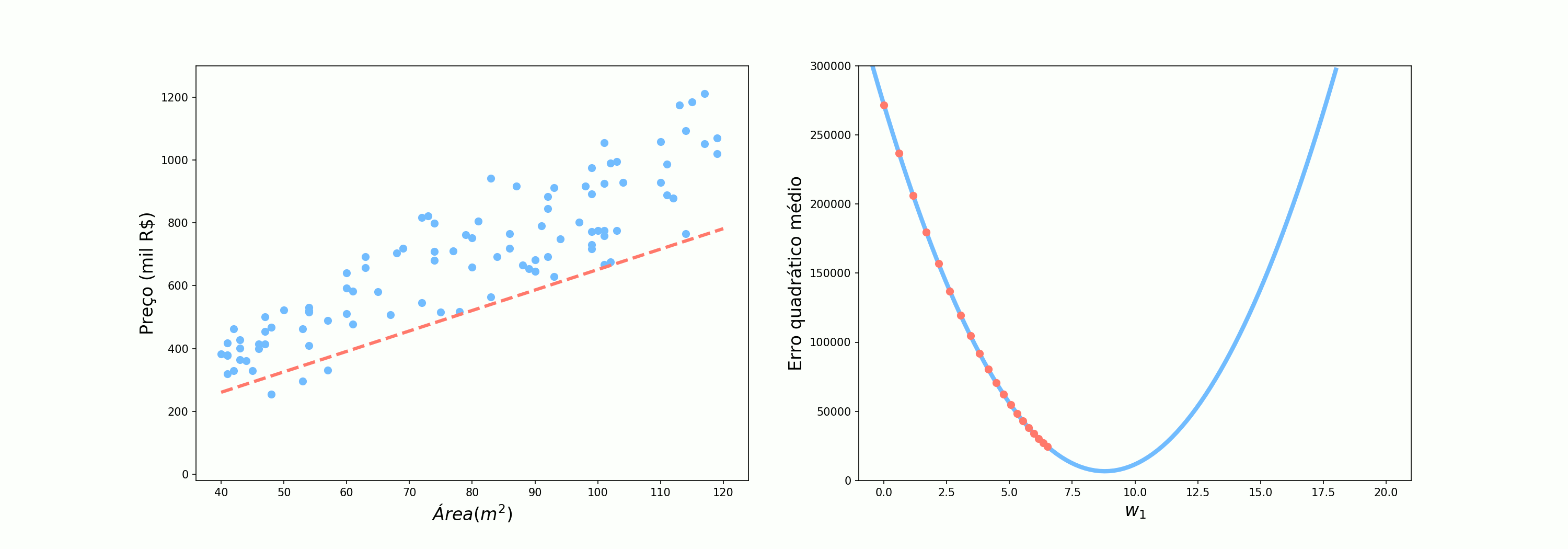
A primeira abordagem que vamos testar utilizar todos os pontos de uma vez. Vamos observar o comportamento dos parâmetros quando utilizamos os erros das 100 previsões para atualizar os pesos. Esse é o cenário em que o Alex perguntava para 10 pessoas antes de seguir seu caminho.
Um ponto de cada vez
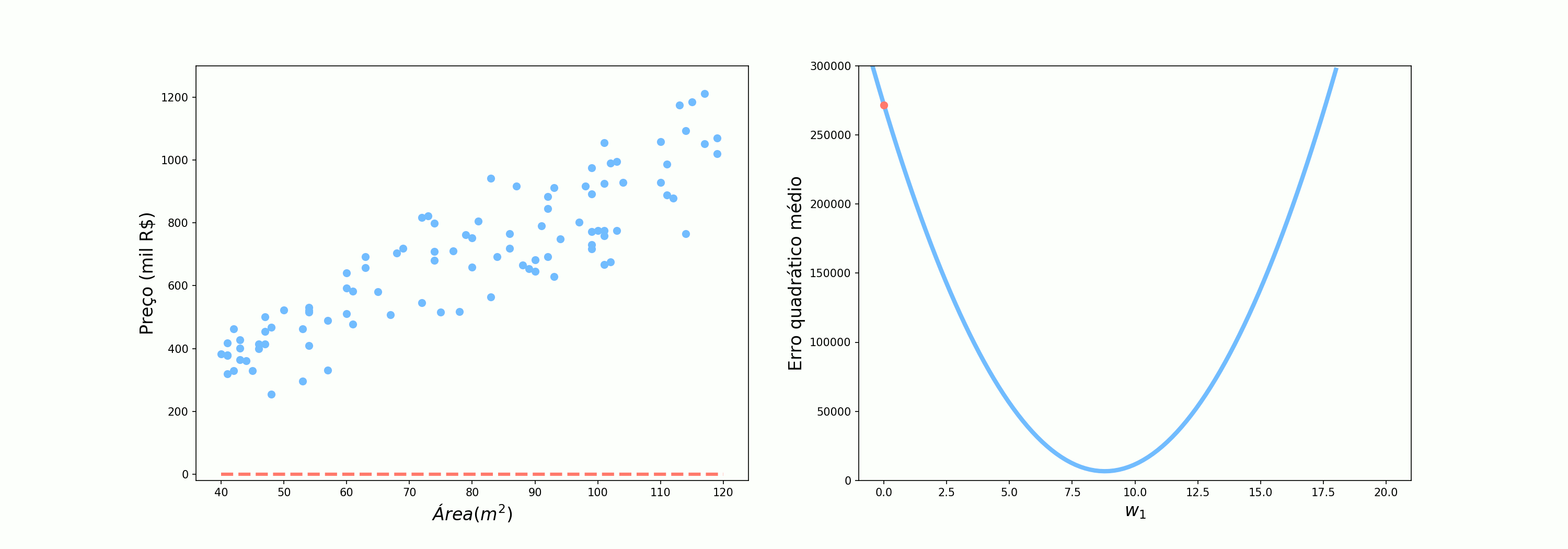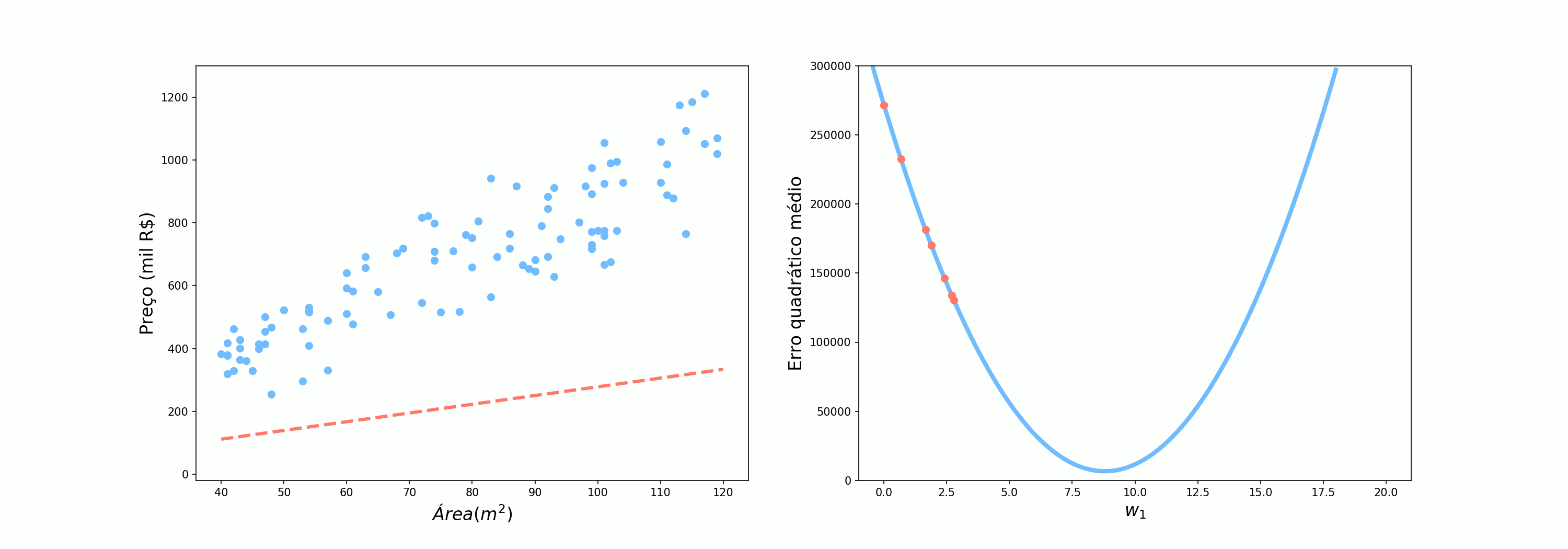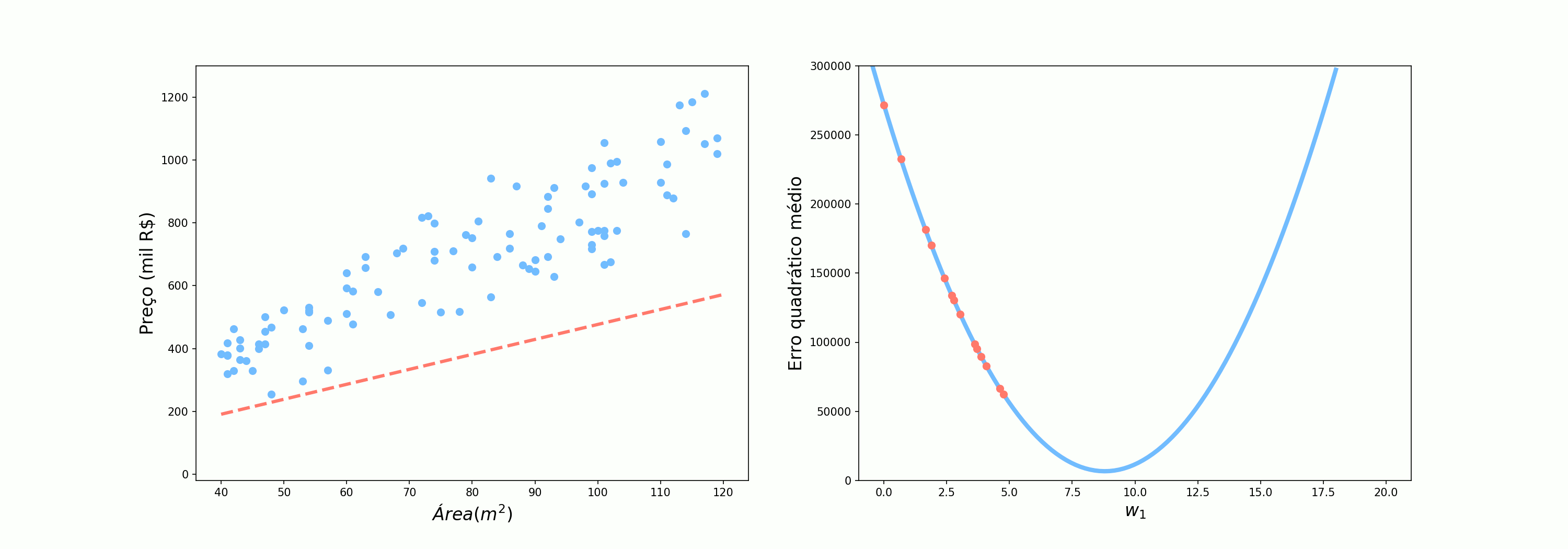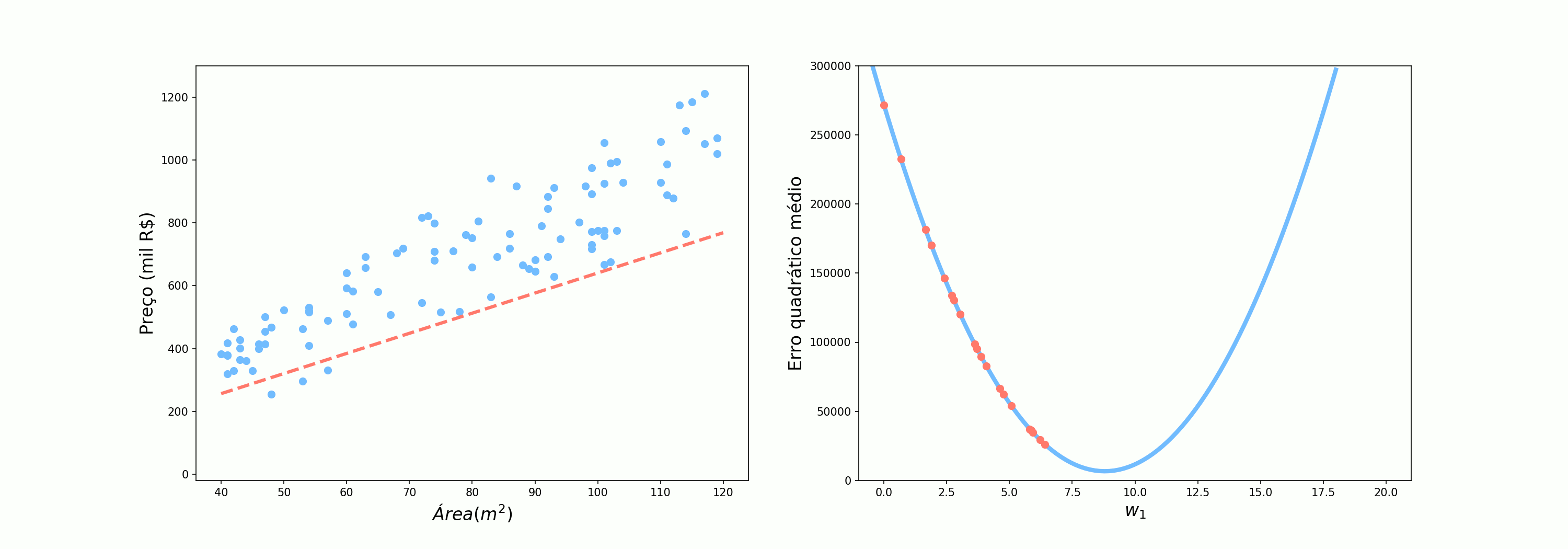
Vamos agora ver como o algoritmo se comporta quando utilizamos um apenas ponto, selecionado aletoriamente, para atualizar os pesos. Como devem ter imaginado, na nossa analogia, esse é o cenário em que o Alex perguntava somente para uma pessoa antes de seguir.
Alguns pontos por vez
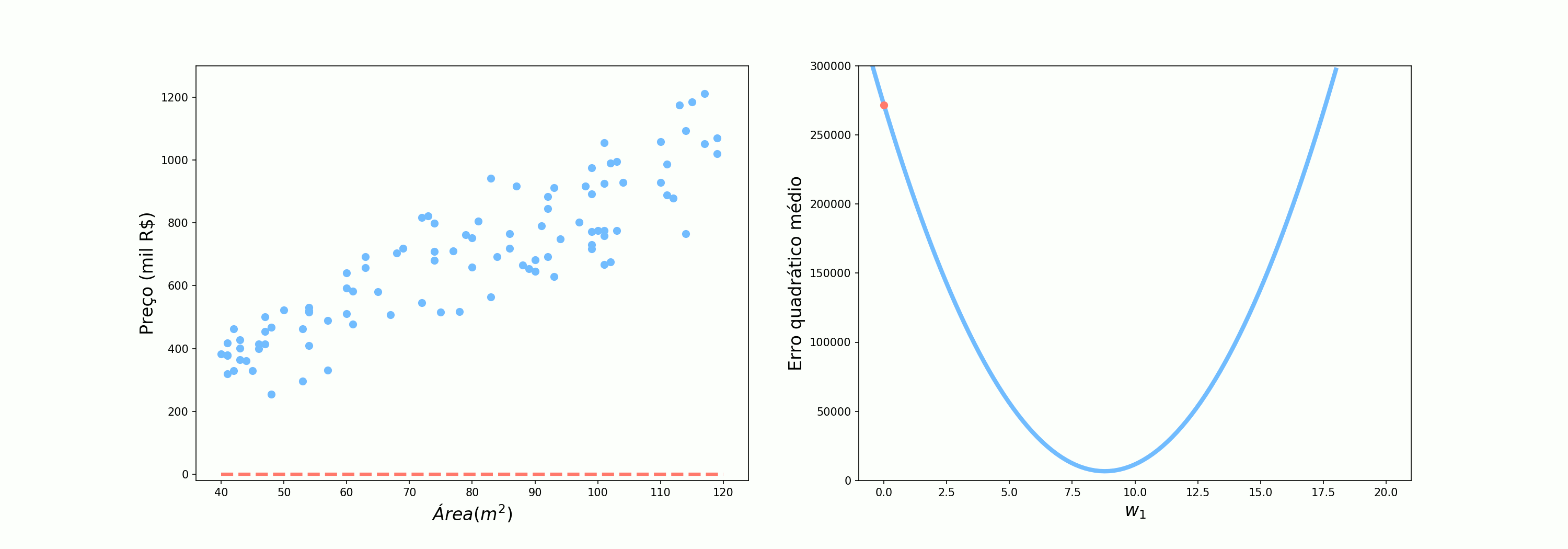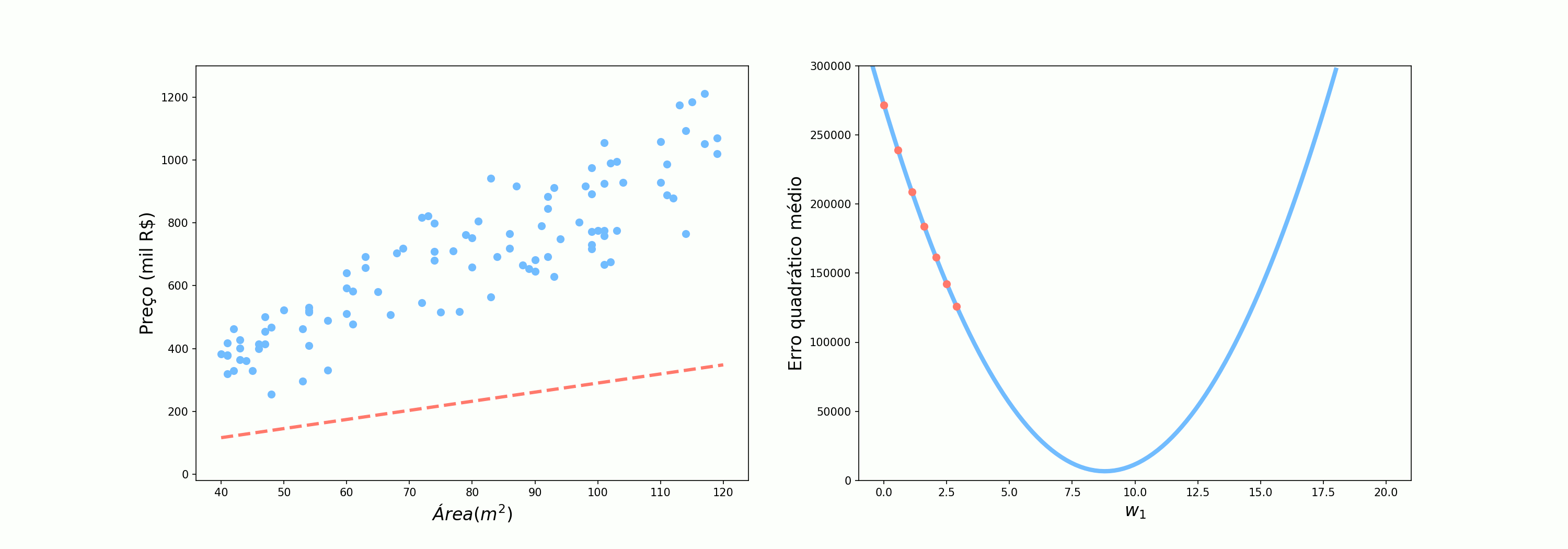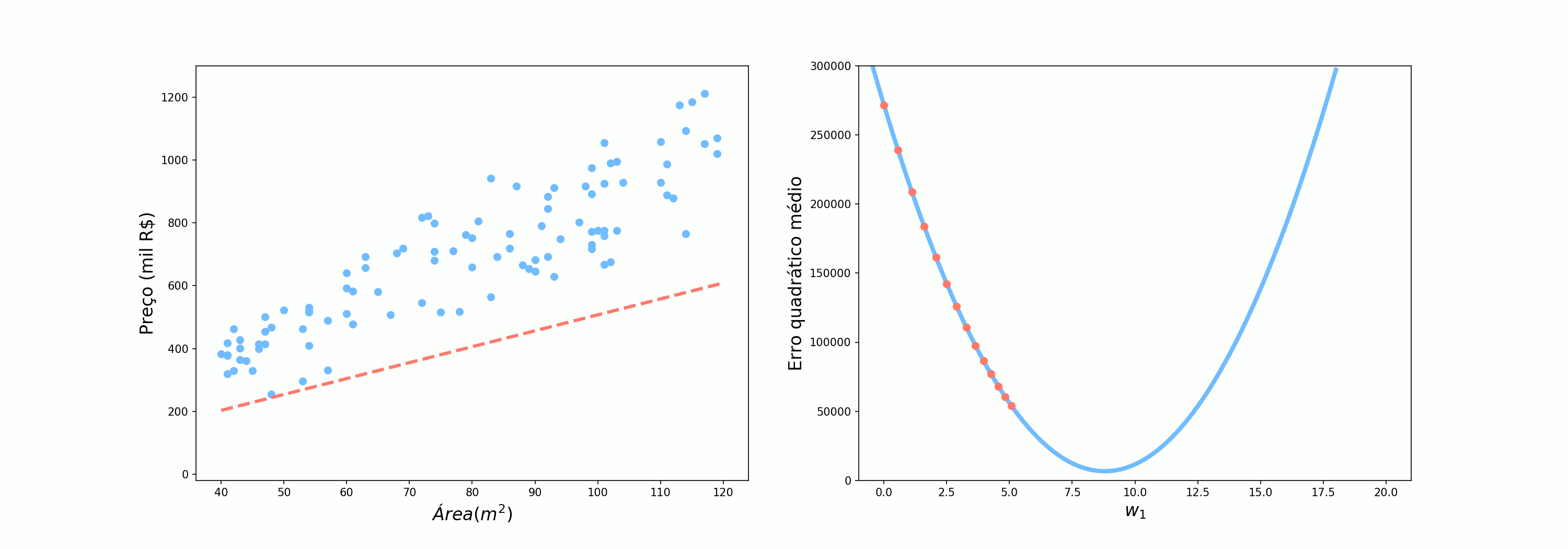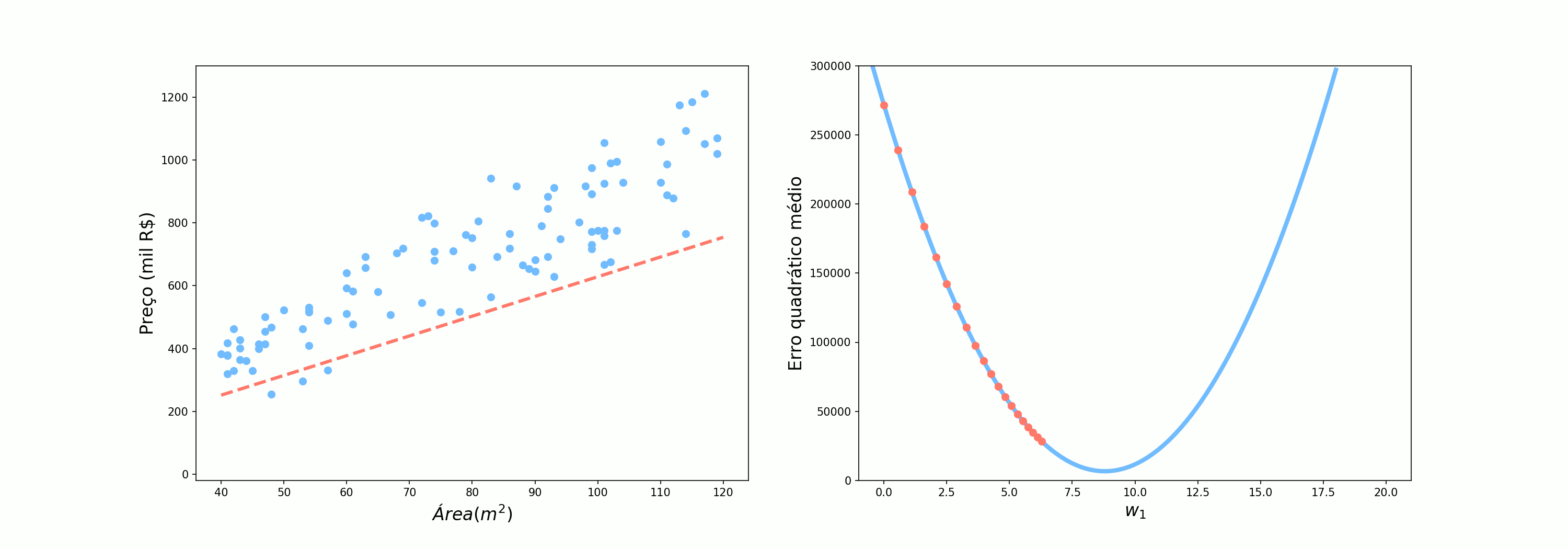
Por fim, vamos analisar como o algoritmo se comporta quando pegamos 10 pontos por vez. Talvez seja óbvio, mas esse é o último cenário vivido por Alex, no qual ele pergunta para 5 pessoas.
Comparando
Se olharmos atentamente ao comportamento do erro nos três cenários, podemos ver claramente que quando utilizamos todos os pontos o comportamento do algoritmo é muito bem comportado, dando “passos” de tamanho ótimo na direção de decrescimento da função. Ao utilizar todos os exemplos o algoritmo tem o nome específico de Gradiente Descendente.
Já quando utilizamos um ponto por vez, o comportamento é muito mais irregular. Apesar de estarmos indo na direção certo, alguns passos são bem curtos enquanto outros são bem longos. Nesse contexto, devido à incerteza associada a cada amostra (ruído, pontos extremos, erro de medição, etc), temos uma incerteza relacionada à previsão de dada amostra e, por isso, chamamos o algoritmo de Gradiente Descendente Estocástico (SGD do inglês Stochastic Gradient Descent). Esse incerteza pode ser relacionado à confusão das pessoas quando Alex perguntava para onde ele devia ir: assim como as pessoas estavam sujeitas a erros, as nossas amostras podem ter medições incorretas, ou terem características um pouco distoantes do restante da distribuição.
O cenário intermediário já nos mostra um comportamento mais regular se comparado ao SGD mas ainda mais incerto do que o Gradiente Descendente completo. Muitas vezes, vamos encontar na literatura esse cenário com o nome de SGD, mas aqui vamos nos referir à ele como Gradiente Descendente com mini lotes (Mini-batch Gradient Descent).
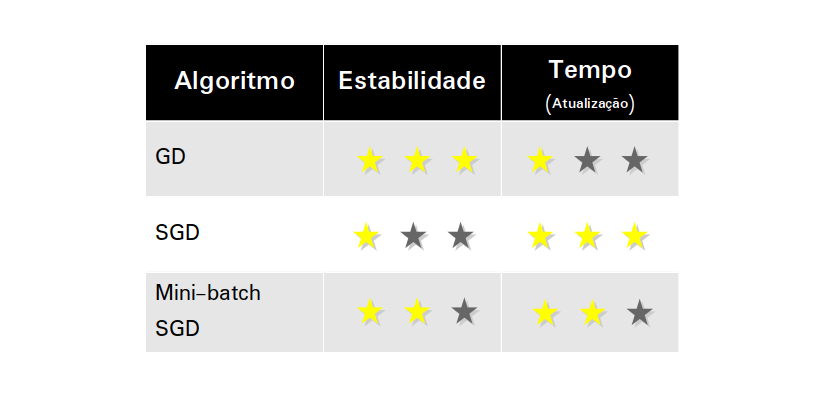
A tabela abaixo sumariza as características de cada um.
E agora?
Por hoje era isso, pessoal. Espero que tenha ficado claro a ideia de quais são as vantagens e desvantagens de cada um dos métodos. No próximo artigo vamos falar um pouco mais sobre algumas funções de ativação. Não perca!