22 min de leitura
Quem bate sou eu!

Quem bate sou eu!
Recentemente, vimos nos noticiários uma certa rixa no elenco do multimiliónario Paris Saint-Germain (PSG) a respeito de quem deveria ser o cobrador oficial de pênaltis da equipe. Desde a renovação com o PSG, Mbappé tem sido o centro das atenções e o principal nome do elenco, mas desde a sua chegada em 2017, Neymar tem sido o cobrador oficial de penalidades do time. A dúvida que surgiu é: qual dos dois é o melhor cobrador de pênaltis? Isto é, será que existe um melhor cobrador entre os dois? Ou ainda, será que o melhor cobrador do PSG é um dos dois mesmo? Afinal temos um elenco recheados de estrelas, como o 6 vezes ganhador da bola de ouro, Lionel Messi. É isso que pretendemos responder nesse artigo! E para isso vamos recorrer à chamada Estatística Bayesiana.
O problema com baixo volume de dados
Antes de começarmos, vou fazer um alerta de que os dados apresentados aqui são só do campeonato francês (Ligue 1) a partir da temporada 17/18, que foi quando Neymar e Mbappé chegaram ao time. Dito isso, podemos começar a análise. A forma mais simples de descobrir se há um melhor cobrador é olhar os número de cobranças contra o número de gols convertidos por cada um. Esses valores estão na tabela abaixo.
| Jogador | Cobranças | Gols | Conversão |
|---|---|---|---|
| Neymar | 26 | 23 | 88,5% |
| Mbappé | 13 | 11 | 84,6% |
Só pela conversão, podemos ver que Neymar seria considerado um melhor cobrador, mas como bons conhecedores da estatística poderíamos nos perguntar: será que essa diferença é significativa? Existem algumas formas de determinar isso na estatística frequentista, sendo a mais usual, os testes de hipótese. O problema dos testes de hipótese é que normalmente eles precisam de um bom volume de dados para serem significativos. E se, por exemplo, quiséssemos comparar um dos dois jogadores com um jogador que acertou 100% das cobranças. Você poderia falar que esse jogador com certeza é melhor, mas e se eu te desse outra informação: ele só bateu 2 pênaltis. Nesse caso, deveríamos ficar em dúvida: será que ele é mesmo um excelente cobrador ou acertou os pênaltis por sorte? Para ter mais certeza, precisaríamos de mais evidências.
Aí vem ela: a distribuição Beta!
Para resolver a essa problema, vamos utilizar o que chamamos de inferência bayesiana e vamos precisar conhecer uma distribuição de probabilidades chamada distribuição Beta. Ela é conhecida como uma distribuição de probabilidades pois o seu intervalo está entre os valores 0 e 1. Ela é muito usada para modelar taxas de conversão como por exemplo a taxa de cliques em anúncios pagos ou até mesmo a taxa de rebatidas de jogadores de baseball. A ideia aqui é dar uma visão geral sobre ela e o que significam seus parâmetros. Vamos começar então com a fórmula matemática da função densidade de probabilidade:
\[f(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{\text{B}(\alpha, \beta)}\] \[\text{B}(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)},\ \Gamma(\alpha) = (\alpha-1)!\]A princípio ela pode parecer bem complicada, com essas funções beta $\text{B}(\alpha, \beta)$ e gamma $\Gamma(\alpha)$, mas vamos ver que a intuição dela não é tão assustadora assim. Para começar, vamos esquecer o denominador $\text{B}(\alpha, \beta)$ da primeira equação. Não é que ele não tenha importância, mas o papel que ele faz é somente de uma constante para que a integral dessa função seja igual a 1 (afinal estamos falando de uma distribuição de probabilidade).
Vamos então nos concentrar no numerador $x^{\alpha-1}(1-x)^{\beta-1}$. Se você tem a sensação de que já viu essa equação em algum lugar, provavelmente você está se lembrando da distribuição binomial, que mede qual a probabilidade de x sucessos em n tentativas de um evento (por exemplo, 5 caras em 10 lançamentos de uma moeda). Dada a probabilidade p de sucesso, a equação da função densidade de probabilidade da binomial é:
\[f(x) = {n \choose x} p^x(1-p)^{n-x}\]Perceba que, apesar de parecidas, elas têm uma importante diferença: na distribuição beta, a probabilidade é tratada como uma variável aleatória, ou seja, o valor x é probabilidade de um sucesso que estamos tentando estimar. Já na distribuição binomial, a probabilidade de sucesso é um parâmetro e o valor x representa o número de sucessos que esperamos. Mas, apesar dessa diferença, olhar as duas pode nos ajudar a ter uma intuição do que os parâmetros da beta significam. Analisando mais atentamente, podemos ver que na binomial a probabilidade de x sucessos é dada por $p^x$. Na beta, esse termo é $x^{\alpha-1}$. Podemos então dizer que $\mathbf{\alpha}-1$ na verdade representa o número de sucessos (no nosso caso gols). Analogamente, $\mathbb{\beta}-1$ representa o número de fracassos, e $(\alpha - 1) + (\beta - 1)= \alpha+\beta-2$ o número total de tentativas.
Ótimo! Entendemos o que siginificam os parâmetros da beta e agora vamos olhar qual o comportamento dessa distribuição:
Código - Betas
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import beta
x_lin = np.linspace(0,1,100)
fig, ax = plt.subplots(figsize=(12,10))
ax.plot(x_lin, beta(5,5).pdf(x_lin), c="xkcd:light blue", lw=2, ls="-", label="B(5,5)")
ax.plot(x_lin, beta(8,2).pdf(x_lin), c="xkcd:orange", lw=2, ls="--", label="B(8,2)")
ax.plot(x_lin, beta(2,8).pdf(x_lin), c="xkcd:turquoise", lw=2, ls="-.", label="B(2,8)")
ax.legend()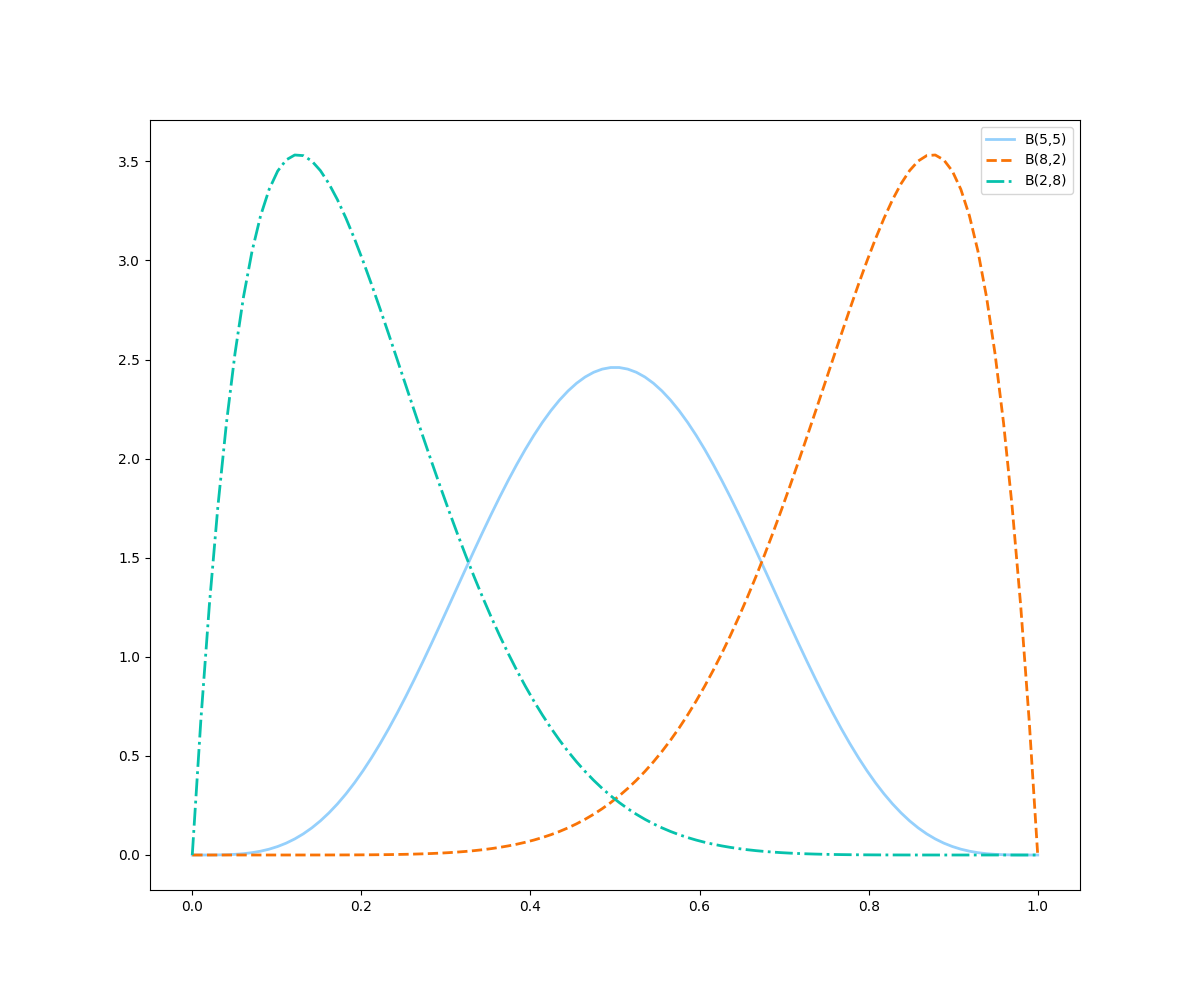
Pela imagem acima, em todos os casos tivemos 10 tentativas, mas no caso em que 8 dos 10 foram sucessos ($B(8,2)$), a curva está muito mais à direita do que no caso em que só tivemos 2 sucessos ($B(2,8)$), ou seja, quanto maior a proporção de sucessos, mais a direita deslocamos a curva. Perceba também que quando tivemos o mesmo número de sucesso e fracassos, a curva ficou bem centralizada. Uma outra curiosidade é o que acontece quando aumentamos o número de eventos.
Código - Variância da beta
x_lin = np.linspace(0,1,100)
fig, ax = plt.subplots(figsize=(12,10))
ax.plot(x_lin, beta(5,5).pdf(x_lin), c="xkcd:light blue", lw=2, ls="-", label="B(5,5)")
ax.plot(x_lin, beta(10,10).pdf(x_lin), c="xkcd:orange", lw=2, ls="--", label="B(10,10)")
ax.plot(x_lin, beta(20,20).pdf(x_lin), c="xkcd:turquoise", lw=2, ls="-.", label="B(20,20)")
ax.legend()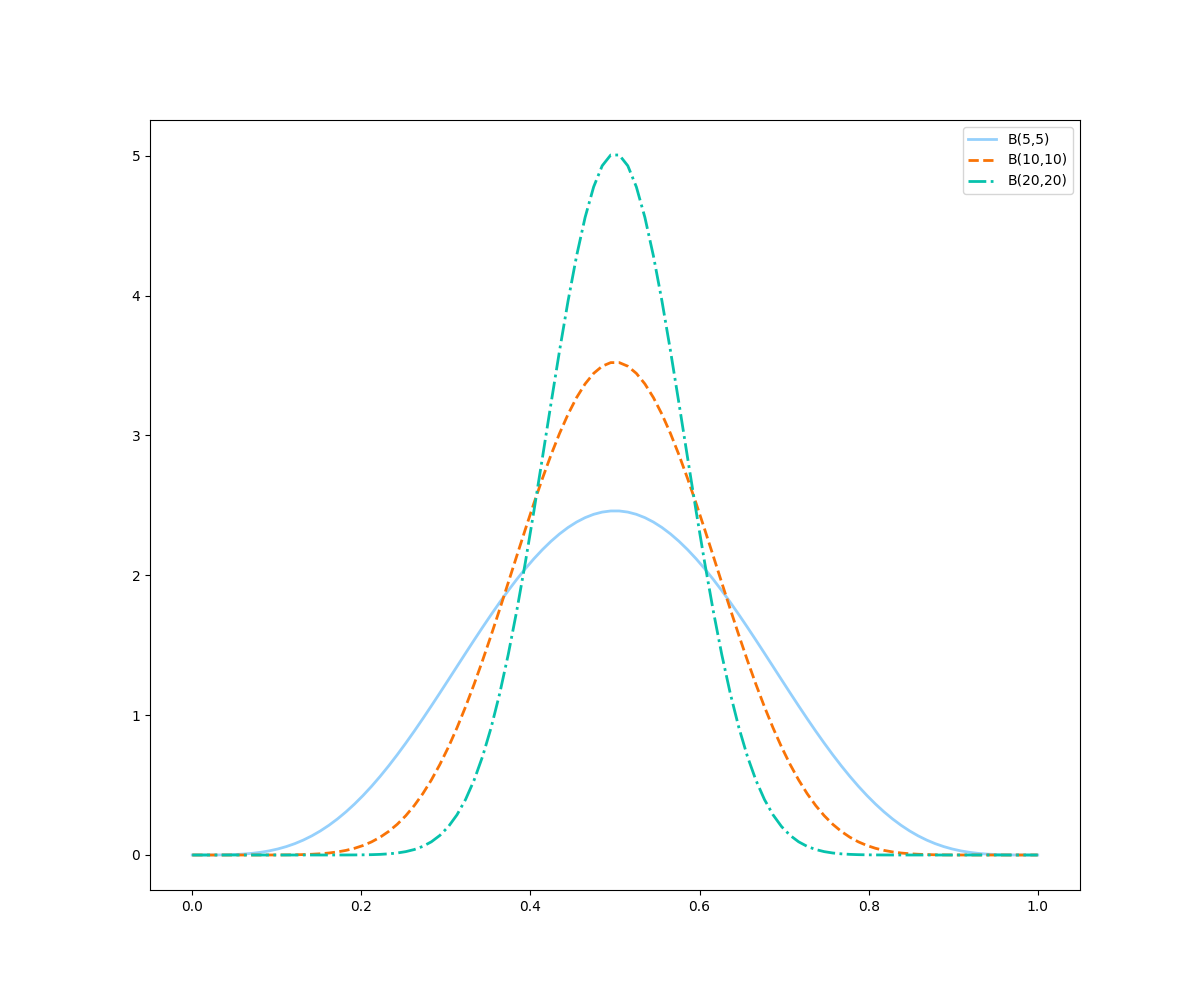
Perceba que as curvas estão centralizadas na mesma posição, pois a taxa de sucesso é a mesma em todas elas (50%). Porém, quanto mais dados temos, mais “finas” essas curvas ficam, ou seja, menor é a variância da distribuição e mais certeza temos que aquele é o valor mais provável de probabilidade.
Apesar de ter essas distribuições ser muito legal, muitas vezes queremos uma estimativa mais pontual do valor da probabilidade. Se você se lembrar das aulas de distribuições de probabilidade, deve pensar em no mínimo 4 métricas para descrever a distribuição. Uma característica muito legal da distribuição beta é que a média (ou esperança da distribuição) é dada por uma equação simples (e que vai ser bem útil):
\[E[x] = \frac{\alpha}{\alpha+\beta}\]Priori e a atualização de expectativa
Excelente! Já temos agora o conhecimento base para introduzirmos outro conceito da inferência bayesiana: a distribuição a priori. Essa distribuição representa nada mais do que uma crença inicial que nós temos. Claramente você não entendeu nada até agora né :? Vamos então tentar colocar num exemplo real. Se um jogador nunca cobrou um pênalti, ou seja, você não tem dado nenhum sobre ele, qual é sua estimativa da probabilidade que ele vá fazer o gol? Isso é o que chamamos de priori!
Você pode ter pensado: “como assim? É só eu chutar uma distribuição?”. É quase isso … Na estatística bayesiana, a definição da priori é uma das tarefas mais importantes pois ela pode determinar o resultado final da análise. Vamos então analisar algumas possibilidades. Suporemos aqui que a chance inicial (média) de um jogador é de 50% para fazer o gol. A primeira priori que podemos testar é a $B(1,1)$, também chamada de não informativa. Se você se lembrar, há pouco dissemos que o $\text{sucessos} = \alpha-1$ e $\text{fracassos} = \beta-1$. Com a $B(1,1)$, não estamos assumindo nada pois tanto o número de sucesso, quanto o de fracassos é 0! Mas também podemos testar outras, como por exemplo $B(2,2)$, ou seja, 1 sucesso e 1 fracasso. Abaixo vemos alguns exemplos.
Código - Priori
x_lin = np.linspace(0,1,100)
fig, ax = plt.subplots(figsize=(12,10))
ax.plot(x_lin, beta(1,1).pdf(x_lin), c="xkcd:light blue", lw=2, ls="-", label="B(1,1)")
ax.plot(x_lin, beta(2,2).pdf(x_lin), c="xkcd:orange", lw=2, ls="--", label="B(2,2)")
ax.plot(x_lin, beta(6,6).pdf(x_lin), c="xkcd:turquoise", lw=2, ls="-.", label="B(6,6)")
ax.plot(x_lin, beta(11,11).pdf(x_lin), c="xkcd:royal purple", lw=2, ls=":", label="B(11,11)")
ax.legend()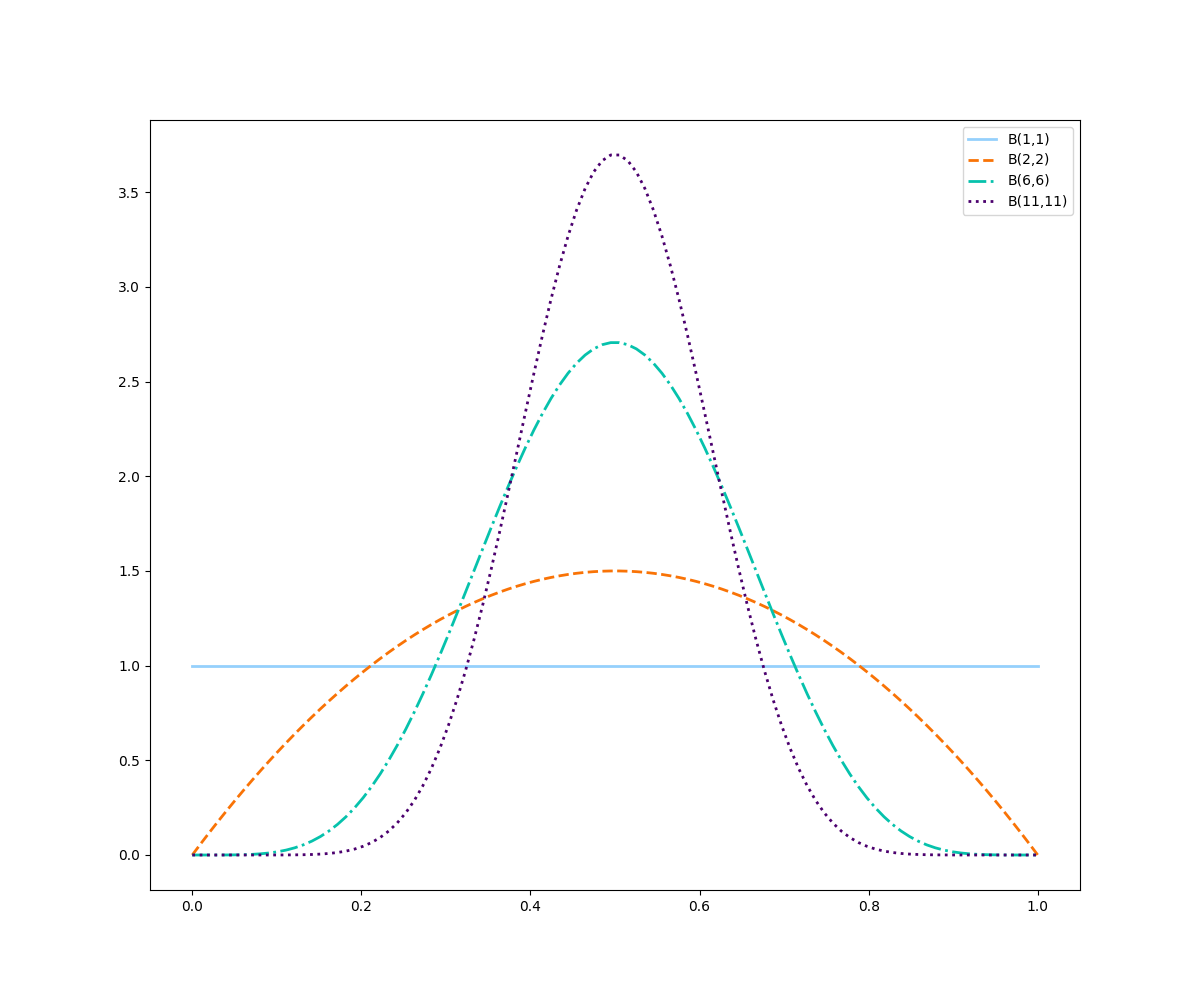
A priori não informativa nos dá uma reta horizontal, ou seja, todos os valores tem a mesma chance de ser a probabilidade real. Perceba também que ao assumirmos que a probabilidade inicial média ($\frac{\alpha}{\alpha+\beta}$) de 50%, temos várias possibilidades de escolha do número de eventos. Todas as curvas acima, tem probabilidade média de 50%! Como então escolher o melhor valor? E no que isso vai impactar?
Para responder essa pergunta, vamos primeiro mostrar como nós atualizamos nossa crença. Dissemos que a priori era um “chute” inicial, mas com o tempo nós começamos a observar mais dados dos atletas. Por exemplo, se um jogador bateu 3 pênaltis e converteu 2, como eu incluo essa informação na distribuição? Acontece, que com a distribuição beta isso é muito simples. Tendo uma priori $B(\alpha_0, \beta_0)$, a distribuição atualizada (chamada de posteriori) vai ter a forma $B(\alpha_0+\text{gols}, \beta_0+\text{erros})$. Vamos ver então como ficaria nosso exemplo.
Código - Posteriori
x_lin = np.linspace(0,1,100)
fig, ax = plt.subplots(figsize=(12,10))
ax.plot(x_lin, beta(3,2).pdf(x_lin), c="xkcd:light blue", lw=2, ls="-", label=r"$B(1,1) \rightarrow B(3,2)$")
ax.plot(x_lin, beta(4,3).pdf(x_lin), c="xkcd:orange", lw=2, ls="--", label=r"$B(2,2) \rightarrow B(4,3)$")
ax.plot(x_lin, beta(6,7).pdf(x_lin), c="xkcd:turquoise", lw=2, ls="-.", label=r"$B(6,6) \rightarrow B(8,7)$")
ax.plot(x_lin, beta(13,12).pdf(x_lin), c="xkcd:royal purple", lw=2, ls=":", label=r"$B(11,11) \rightarrow B(13,12)$")
ax.legend()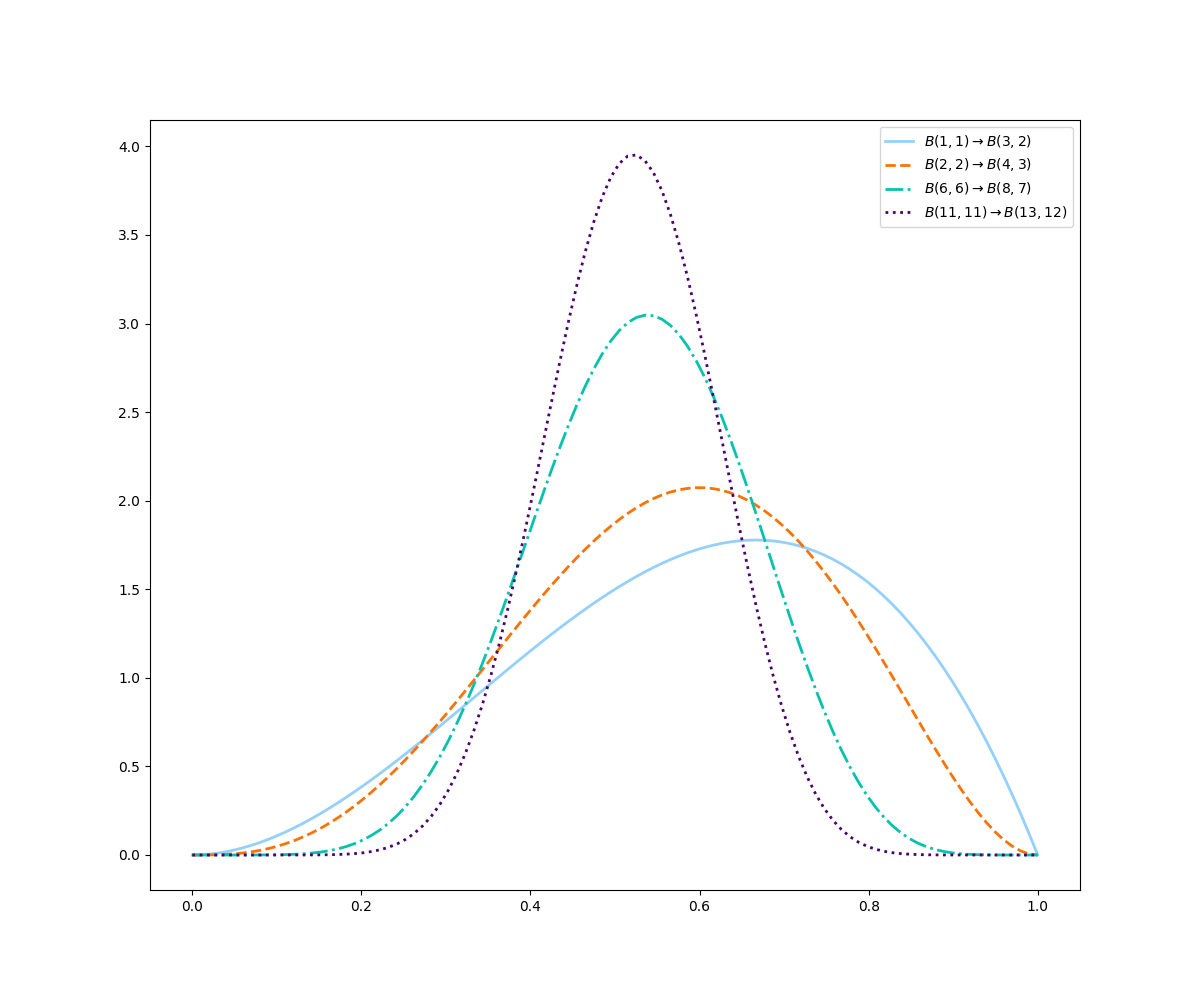
Observe que quanto menos eventos tinhamos na priori ($\alpha_0+\beta_0$), mais fácil é mudar a curva de lugar. A curva com priori $B(1,1)$ foi a mais deslocada, enquanto a curva com priori $B(11,11)$ praticamente ficou no mesmo lugar. Uma priori com poucos eventos chamamos de “fraca”, pois poucas novas evidências conseguem modificá-la. No outro lado, temos a priori “forte”, em que precisamos de muitos eventos para modificá-la. A implicação disso é que se escolhermos uma priori muito fraca, não estamos dando nenhuma informação, e se escolhermos uma muito forte estamos dando informação demais e a curva não irá se alterar.
Neymar vs Mbappé: a hora da verdade!
Chega de enrolação! Vamos logo fazer a comparação que estamos esperando! Primeira coisa: vamos criar nossa priori. Como temos dados de todas as cobranças do campeonato francês, podemos ter uma estimativa da média de conversão e usar isso como estimativa inicial.
Código - Estimativa Conversão
import pandas as pd
data = pd.read_csv("Ligue 1 - Penalties.csv")
data.columns = [col.replace(" ", "_").lower() for col in data.columns]
grouped_data = data.groupby("name").sum()[["penalty_goals", "penalties_taken", "penalty_won"]]
grouped_data["conversion"] = (grouped_data["penalty_goals"]/grouped_data["penalties_taken"]).fillna(0)
mean_prior = grouped_data.sum()["penalty_goals"]/grouped_data.sum()["penalties_taken"]
print(f"Número de cobranças: {grouped_data.sum()['penalties_taken']}")
print(f"Número de Goals: {grouped_data.sum()['penalty_goals']}")
print(f"Conversão: {mean_prior}")Desde a temporada 17/18, tivemos 669 cobranças de pênalti com 529 gols, resultando em uma conversão de aproximadamente 80%. Ótimo! Agora que sabemos a conversão precisamos criar nossa priori. Vamos supor que um bom número de cobranças seja 5, ou seja, queremos que $\alpha_0+\beta_0 - 2 = 5$. Dessa forma, estimamos que $\alpha_0=5$ e $\beta_0=2$. Esse valor foi escolhido pelo que eu achei que fazia sentido, mas perceba que existe uma razão para não usarmos 669 cobranças: com esse número a priori seria tão forte que, dificilmente, algum jogador conseguiria alterar sua curva.
\[\alpha_0 = (5*0.8) + 1 = 5\] \[\beta_0 = 5 - (5*0.8) + 1 = 2\]Código - Priori cobranças de pênalti
n_eventos = 10
alpha_0 = n_eventos*round(mean_prior,1) + 1
beta_0 = n_eventos - n_eventos*round(mean_prior,1) + 1
print(alpha_0, beta_0)Estamos chegando a algum lugar! Depois de calcular a priori, podemos atualizá-la com os dados de cobranças dos dois jogadores. Lembre-se que para atualizar a priori, basta criarmos uma nova beta com $\alpha = \alpha_0 + \text{gols}$ e $\beta = \beta_0 + \text{tentativas-gols}$.
| Jogador | Cobranças | Gols | Conversão real | $\alpha_0$ + Gols | $\beta_0$ + (Cobranças - Gols) | Conversão estimada |
|---|---|---|---|---|---|---|
| Neymar | 26 | 23 | 88,5% | 28 | 5 | 84,5% |
| Mbappé | 13 | 11 | 84,6% | 16 | 4 | 80% |
Código - Neymar vs Mbappé
x_lin = np.linspace(0,1,100)
fig, ax = plt.subplots(figsize=(12,10))
ax.plot(x_lin, beta(9,3).pdf(x_lin), c="xkcd:dark gray", lw=2, ls="-", label="Priori")
ax.plot(x_lin, beta(28,5).pdf(x_lin), c="xkcd:jade", lw=2, ls="--", label="Neymar")
ax.fill_between(x_lin, 0, beta(28,5).pdf(x_lin), color="xkcd:jade", alpha=0.4)
ax.plot(x_lin, beta(16,4).pdf(x_lin), c="xkcd:marine blue", lw=2, ls="-.", label="Mbappé")
ax.fill_between(x_lin, 0, beta(16,4).pdf(x_lin), color="xkcd:marine blue", alpha=0.4)
ax.legend()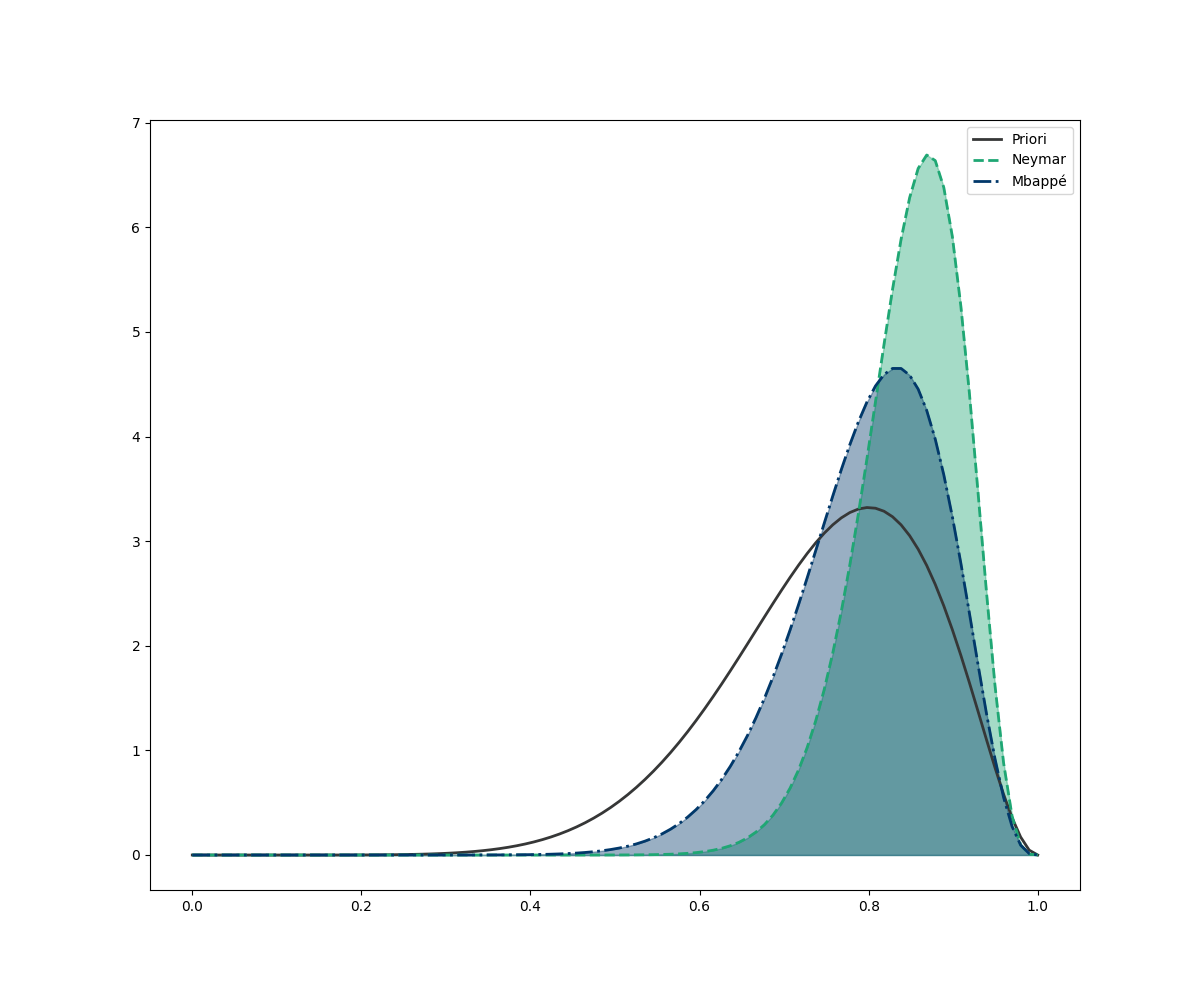
Pela nossa nova estimativa, o Neymar ainda é um cobrador melhor que o Mbappé, convertendo 4% a mais das cobranças. Entretanto, se observarmos as curvas, vemos que temos uma grande intersecção entre elas. Qual será o nosso nível de confiança de que o Neymar é realmente melhor?
O teste AB Bayesiano (ou quase)
Para tentar estimar essa probabilidade de que o Neymar seja realmente melhor, vamos usar uma estratégia muito comum nos teste AB. Não vamos entrar no detalhe sobre o que é um teste AB, nem como mensurá-lo. A ideia é tomar emprestada uma estratégia para compararmos duas distribuições. A receita é bem simples:
- Estime as duas distribuições que você quer comparar;
- Retire uma amostra suficientemente grande de cada uma delas;
-
Compare a primeira amostra da distribuição 1 com a primeira amostra da distribuição 2, a segunda com a segunda, e assim por diante;
a. Para cada comparação, veja qual distribuição tem a maior amostra;
- A proporção de vitórias de distribuição 1 é a probabilidade de essa distribuição ser melhor que a distribuição 2.
Fazendo essa amostragem, estimamos que a chance de o Neymar ser um melhor cobrador que o Mbappé é de 67%! Nada mal, não é mesmo!
Código - Teste AB
n_samples = 1_000_000
samples_neymar = beta(28,5).rvs(n_samples)
samples_mbappe = beta(16, 4).rvs(n_samples)
(samples_neymar - samples_mbappe > 0).sum()/n_samplesO melhor de todos
Uma outra dúvida que tínhamos era se esses eram realmente os dois melhores cobradores do PSG. Para responder a essa pergunta, vamos precisar utilizar outros dados além do que temos aqui. Como Neymar e Mbappé cobraram praticamente todos os pênaltis do PSG no campeonato francês desde que chegaram, vamos utilizar dados de toda a carreira dos outros jogadores. Esses dados forma obtidos do site Transfer Market. Vamos analisar 4 jogadores: Neymar, Mbappé, Messi e Pablo Sarabia (você já verá o porquê!).
| Jogador | Cobranças | Gols | Conversão |
|---|---|---|---|
| Neymar | 87 | 72 | 82,7% |
| Mbappé | 25 | 20 | 80% |
| Messi | 134 | 104 | 77,6% |
| Sarabia | 16 | 16 | 100% |
Pela tabela acima, Sarabia parece ser o melhor cobrador, mas vamos ver como ficariam as estimativas das betas para esses jogadores com esses dados.
Código - Posterior melhor cobrador
alpha_neymar = alpha_0 + 72
beta_neymar = beta_0 + 15
alpha_mbappe = alpha_0 + 20
beta_mbappe = beta_0 + 5
alpha_sarabia = alpha_0 + 16
beta_sarabia = beta_0 + 0
alpha_messi = alpha_0 + 104
beta_messi = beta_0 + 30
x_lin = np.linspace(0,1,100)
fig, ax = plt.subplots(figsize=(12,10))
ax.plot(x_lin, beta(9,3).pdf(x_lin), c="xkcd:dark gray", lw=2, ls="-", label="Priori")
ax.plot(x_lin, beta(alpha_neymar,beta_neymar).pdf(x_lin), c="xkcd:jade", lw=2, ls="--", label="Neymar")
ax.fill_between(x_lin, 0, beta(alpha_neymar,beta_neymar).pdf(x_lin), color="xkcd:jade", alpha=0.4)
ax.plot(x_lin, beta(alpha_mbappe, beta_mbappe).pdf(x_lin), c="xkcd:marine blue", lw=2, ls="-.", label="Mbappé")
ax.fill_between(x_lin, 0, beta(alpha_mbappe, beta_mbappe).pdf(x_lin), color="xkcd:marine blue", alpha=0.4)
ax.plot(x_lin, beta(alpha_sarabia, beta_sarabia).pdf(x_lin), c="xkcd:salmon", lw=2, ls="-.", label="Sarabia")
ax.fill_between(x_lin, 0, beta(alpha_sarabia, beta_sarabia).pdf(x_lin), color="xkcd:salmon", alpha=0.4)
ax.plot(x_lin, beta(alpha_messi, beta_messi).pdf(x_lin), c="xkcd:sky blue", lw=2, ls="-.", label="Messi")
ax.fill_between(x_lin, 0, beta(alpha_messi, beta_messi).pdf(x_lin), color="xkcd:sky blue", alpha=0.4)
ax.legend()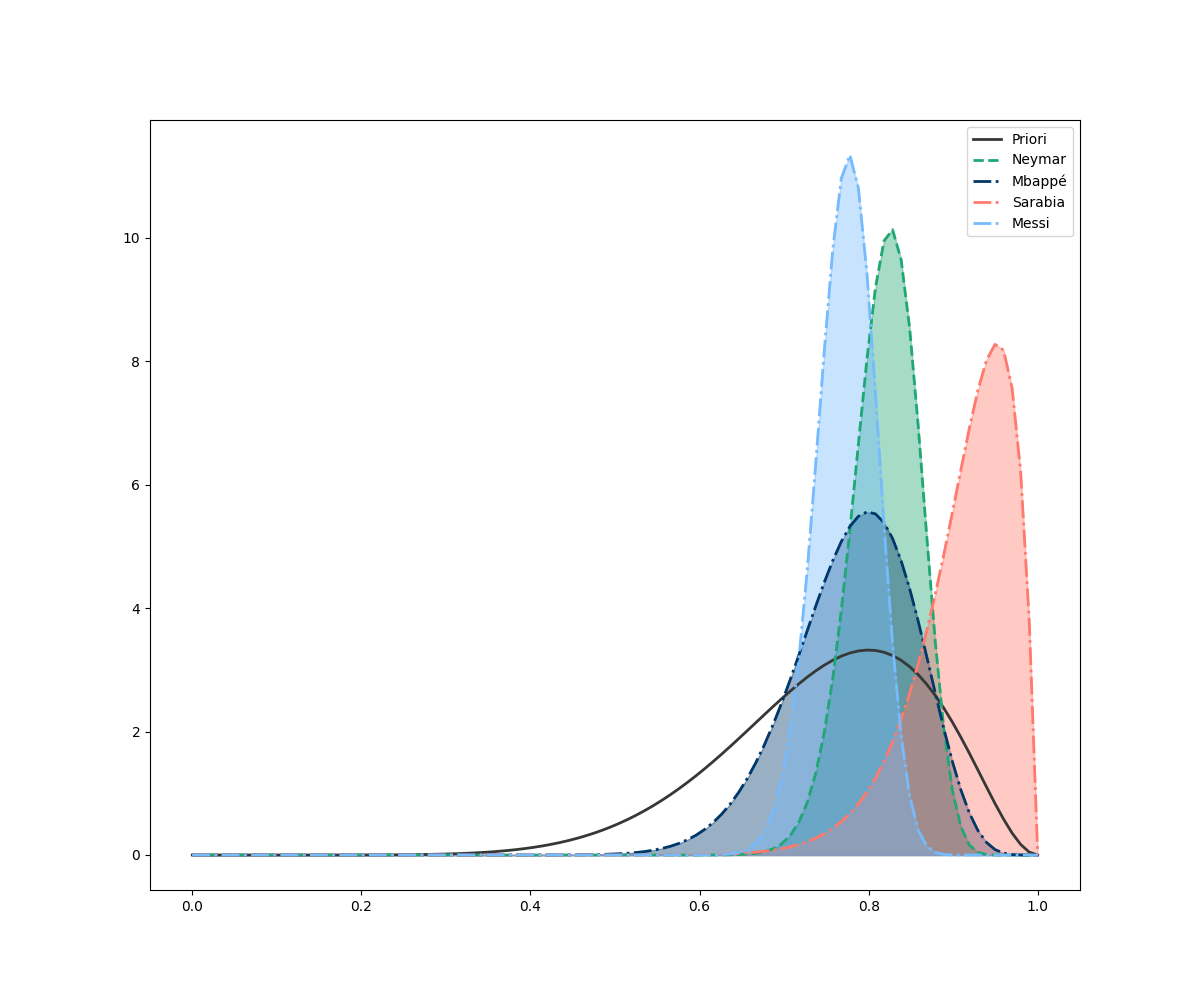
Sarabia continua na frente! Logo atrás temos o Neymar, mas vamos ver qual a probabilidade do Sarabia ser melhor cobrador que o Neymar. Utilizando novamente o teste AB, vemos que a probabilidade de isso acontecer é de 90%! Os dados estão no dizendo que a escolha mais lógica como batedor de pênaltis oficial do time deveria ser ninguém mais, ninguém menos que Pablo Sarabia!
Código - Teste AB Neymar vs Sarabia
n_samples = 1_000_000
samples_neymar = beta(alpha_neymar,beta_neymar).rvs(n_samples)
samples_sarabia = beta(alpha_sarabia, beta_sarabia).rvs(n_samples)
(samples_sarabia - samples_neymar > 0).sum()/n_samplesConclusão
A ideia de artigo foi usar essa polêmica recente para introduzir os conceitos da inferência bayesiana. Vimos o que é a distribuição beta e como ela se encaixa no nosso problema, como estimar a priori, como atualizar nossas crenças e como verificar a probabilidade de uma distribuição ser melhor do que a outra. Claro que isso tudo foi só uma introdução e existem muito mais conceitos para serem entendidos. Para quem quiser brincar um pouco, estou disponibilizando os dados usados nessa análise. Por hoje é isso, pessoal! Espero que tenham gostado!

