8 min de leitura

Uma introdução a Redes Neurais

Featured image

Fala, pessoal! Hoje vamos falar um pouco sobre o que talvez seja o modelo mais comentado atualmente quando falamos de Inteligência Artificial: as famosas Redes Neurais. Apesar de bastante conhecidas, muitos acreditam que seu funcionamento é muito complexo para ser entendido e preferem acreditar que se trata de uma "caixa preta" ou "mágica". O objetivo dessa série de artigos é mostrar como realmente esse algoritmo funciona e que não é nenhum "ser sobrenatural".

Nesse primeiro artigo, vamos estudar quais elementos compõem um rede neural e como podemos utilizá-los para realizar previsões.

O que são Redes Neurais?

Antes de mais nada vamos começar dando uma visão geral dos componentes de uma Rede Neural:

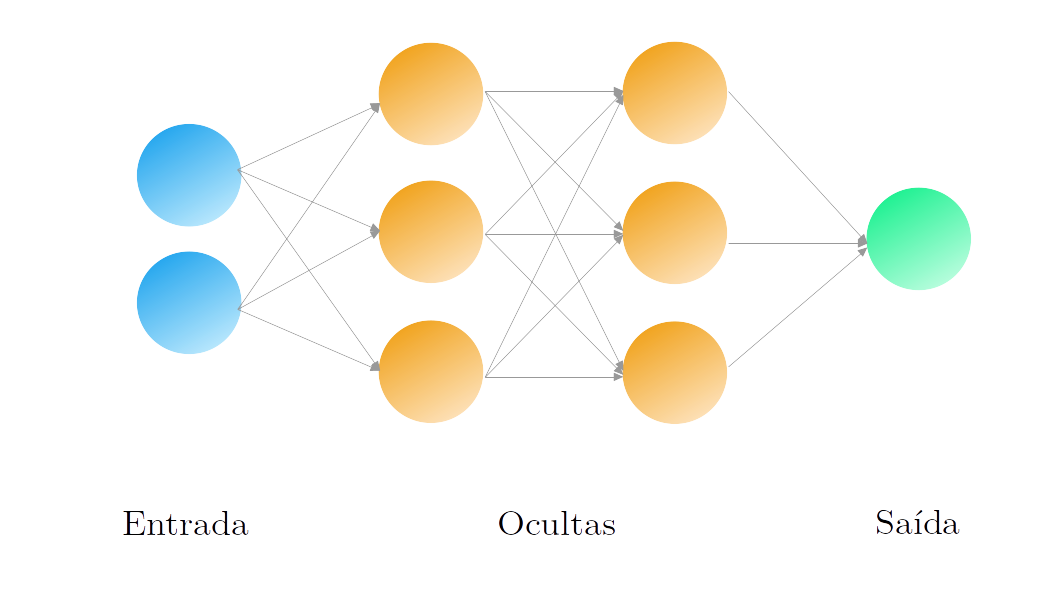
A imagem acima mostra uma arquitetura genérica para redes neurais na qual podemos ver claramente 3 estruturas:

  1. Camada de entrada (em azul): essa é estrutura responsável por receber as informações que queremos utilizar como variáveis explicativas do nosso modelo;
  2. Camada de saída (em verde): estrutura final da rede, responsável por dar a previsão final em que estamos interessados;
  3. Camadas ocultas (em laranja): são representações intermediárias que auxiliam na passagem do nosso conjunto de dados de entrada para a nossa saída. São chamadas ocultas pois as saídas dessas camadas não são vistas pelos usuários finais.

As camadas são as estruturas macro da rede. Mas do que elas são compostas?

O elemento básico de uma camada é chamado de neurônio (por isso o algoritmo se chama redes neurais). Um neurônio nada mais é do que uma combinação linear (o que??) de suas entradas seguida pela aplicação de uma função de ativação. Falamos vários termos técnicos, mas o que realmente isso quer dizer?

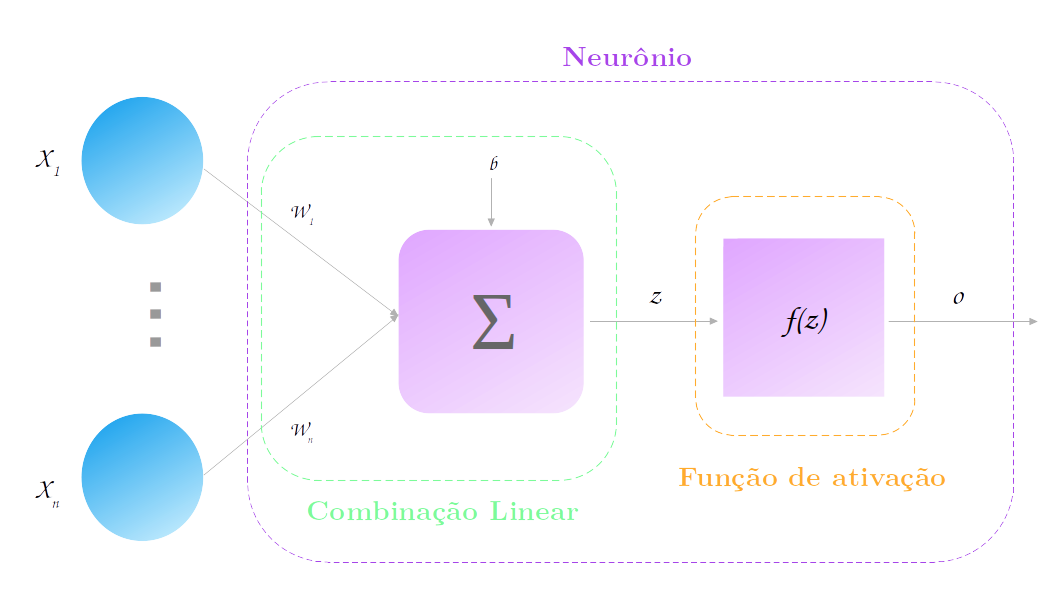
Combinação Linear

Uma combinação linear significa que vamos multiplicar cada valor de entrada $X_i$ por um outro valor $w_i$, denominado peso, e depois somar todos os resultados dessa multiplicação. Além de somarmos os valores de entrada multiplicados pelos seus pesos, também somamos um valor constante:

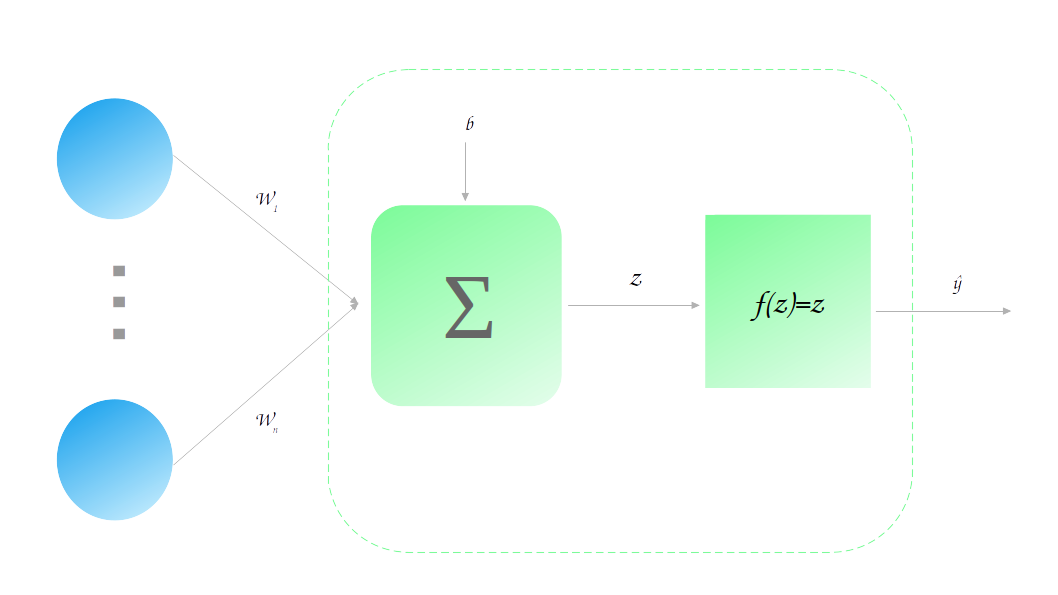
\[\large c(X_1, ..., X_n) = b\ +\ w_1X_1\ +\ w_2X_2\ +\ ...\ +\ w_nX_n\]

Mas espere um pouco, essa não é uma equação conhecida? Exatamente: esse é a equação do algoritmo de Regressão Linear!!! Uma regressão linear nada mais é do que uma combinação linear das variáveis de entrada. E uma regressão linear também pode ser vista como uma rede neural muito simples: não temos camadas escondidas, a camada de saída tem somente um neurônio e a função de ativação dele é a função identidade $f(z) = z$.

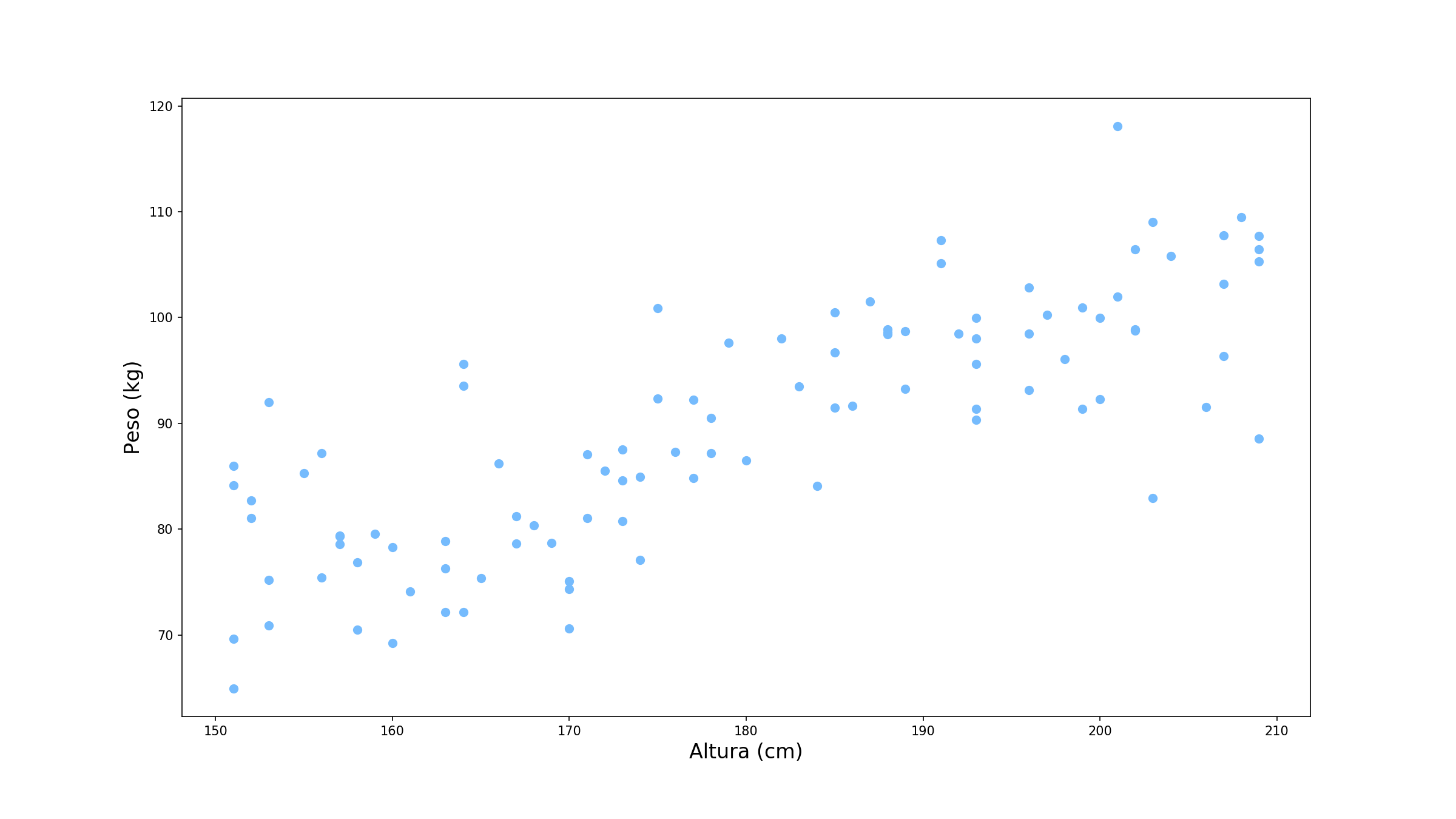
Vamos usar um exemplo prático. Suponha que queremos prever o peso de uma pessoa sabendo sua altura. Nossos dados estão dispostos como abaixo:

Nessa caso, temos uma única variável explicativa, a altura, e a nossa variável alvo é o peso. Assim nossa rede neural assume a seguinte forma:

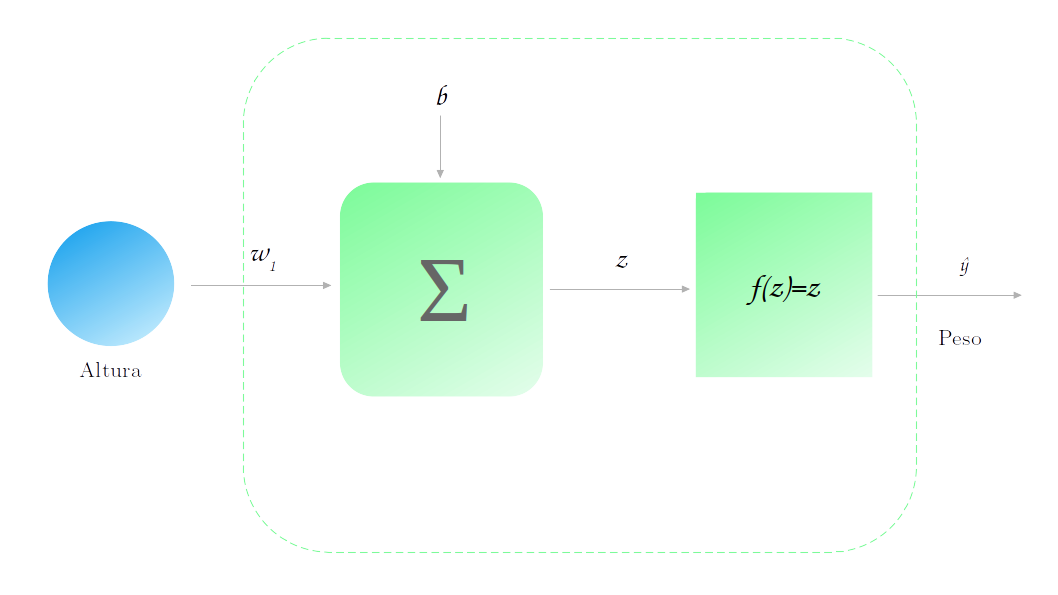
Vamos supor também que nosso modelo já foi treinado (mostraremos em outro post como esse treino é realizado) e que obtemos os seguintes parâmetros: $w_1 = 0.43$ e $b=12$. Vamos utilizar o nosso modelo para realizar uma previsão sobre o peso de uma pessoa com 177 cm de altura. Para fazer isso, basta multiplicarmos a nossa altura, 177 cm, por 0.43 e somarmos 12, resultando em 88.1. Também precisamos passar esse resultado pela função de ativação, que no caso é a identidade e então nós temos que a previsão final é 88.1 kg.

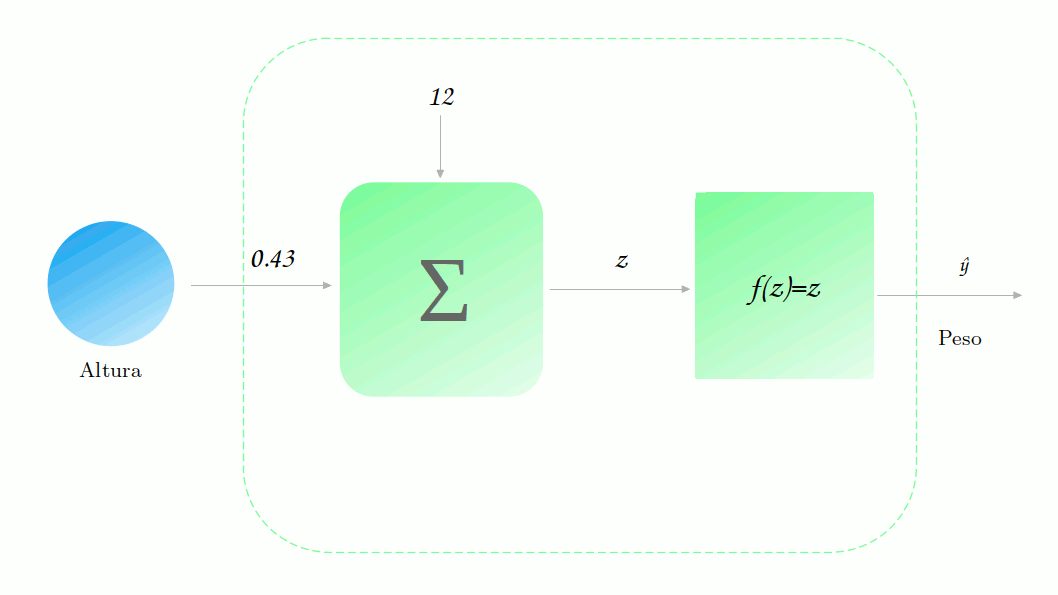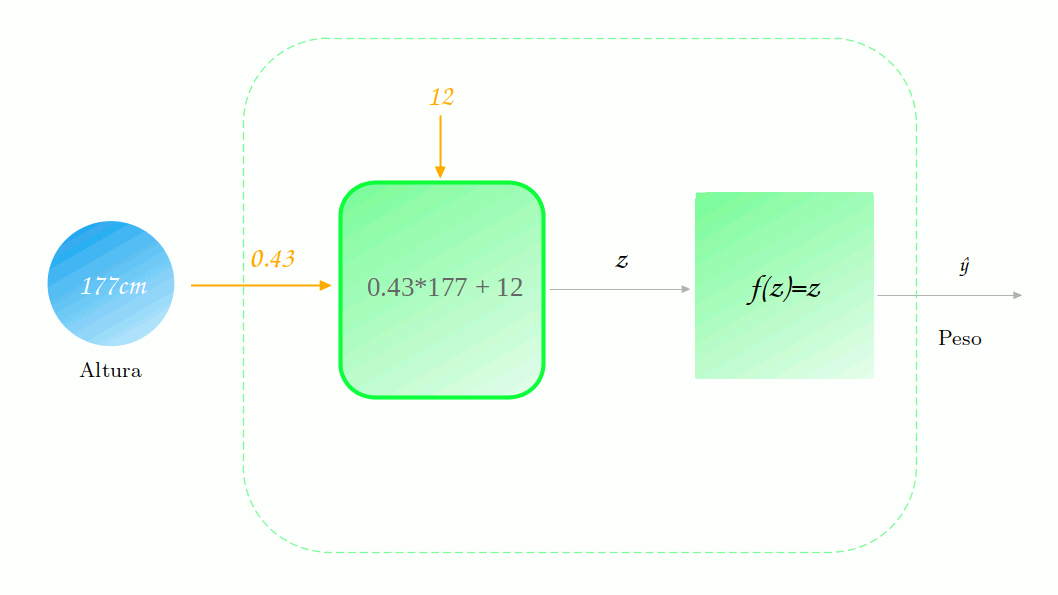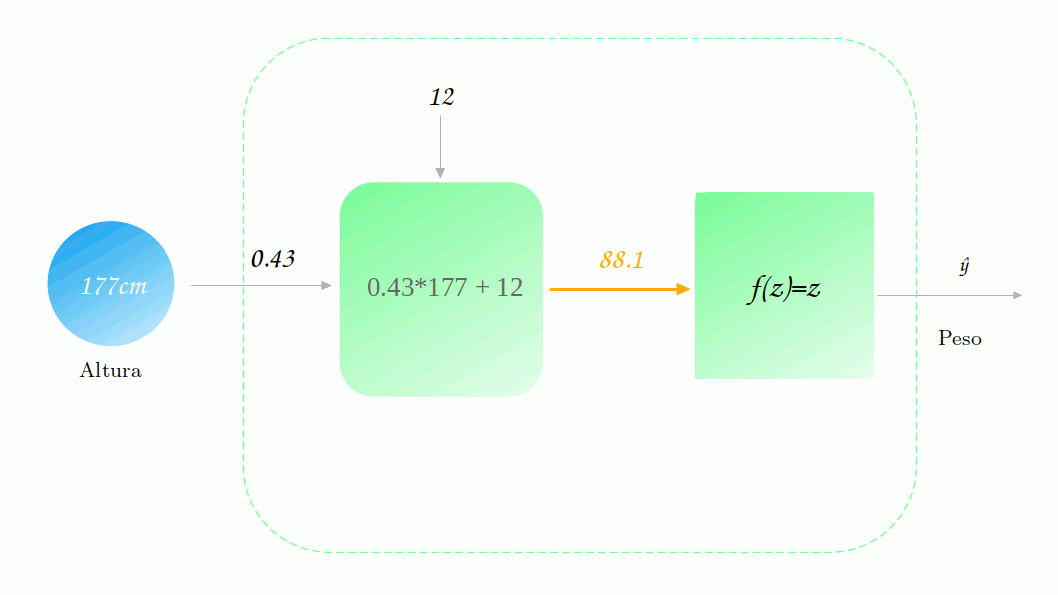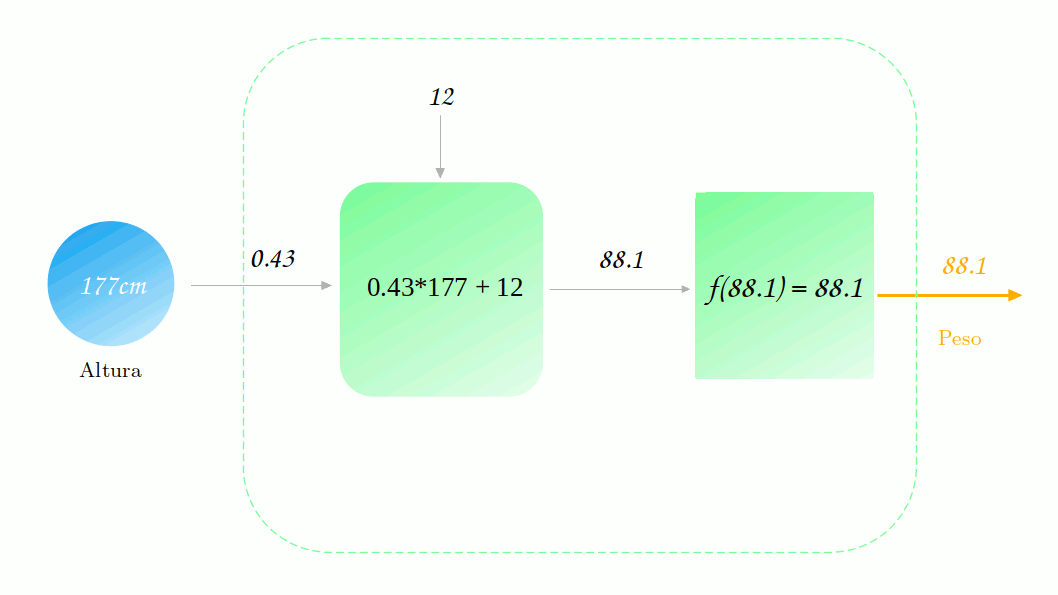
Muito simples não é mesmo, mas vamos adicionar um pouco mais de complexidade aqui.

Funções de ativação

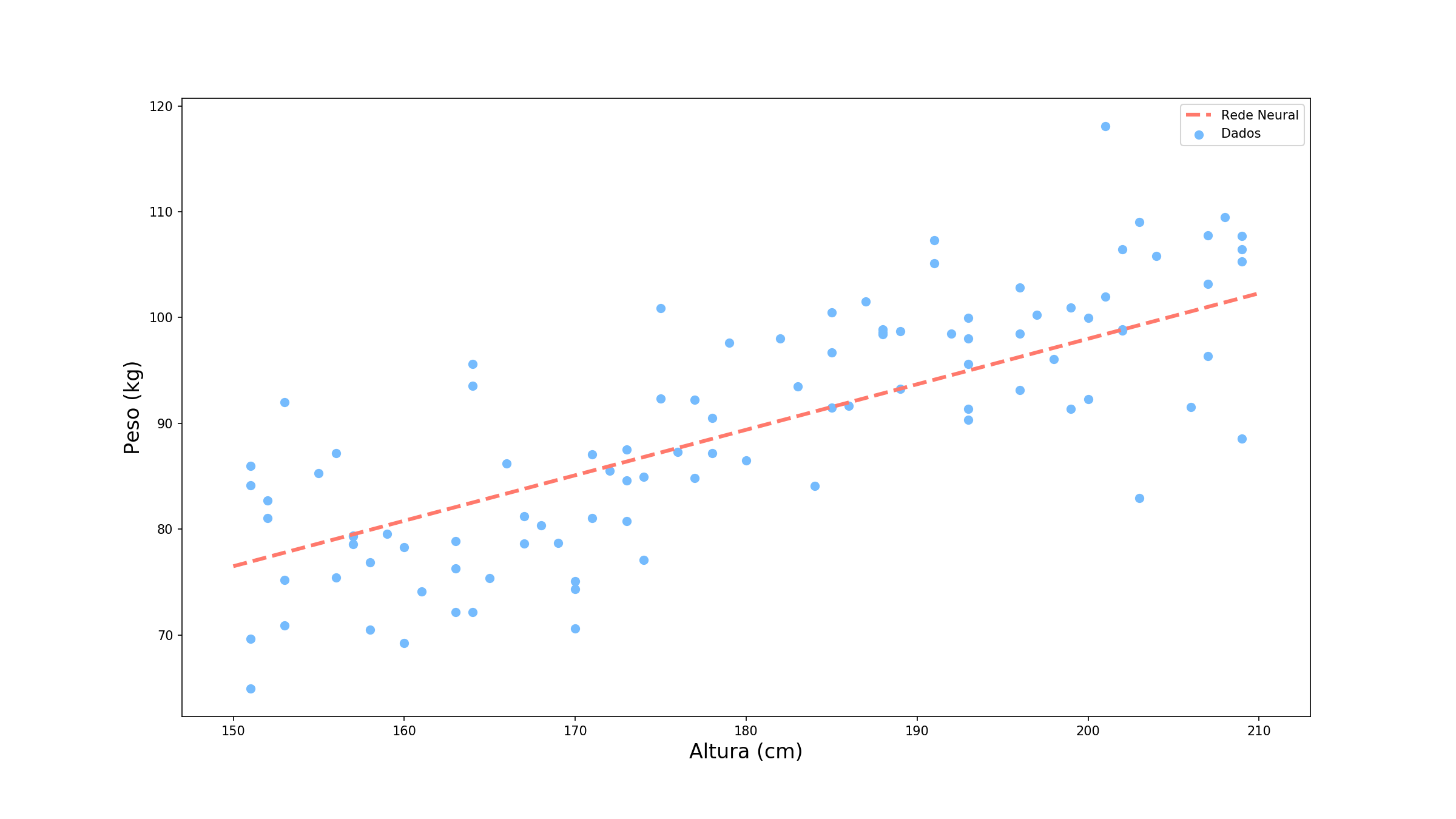
Quando analisamos os dados do nosso problema, podemos perceber que existe uma relação linear entre a altura e o peso. O nosso modelo anterior, com um único neurônio e função de ativação identidade tem justamente o formato de uma reta (ou um hiperplano em problemas com mais variáveis), como podemos ver abaixo.

Mas e se por acaso tivemos um outro problema, dessa vez de classificação, que se comporta da seguinte maneira:

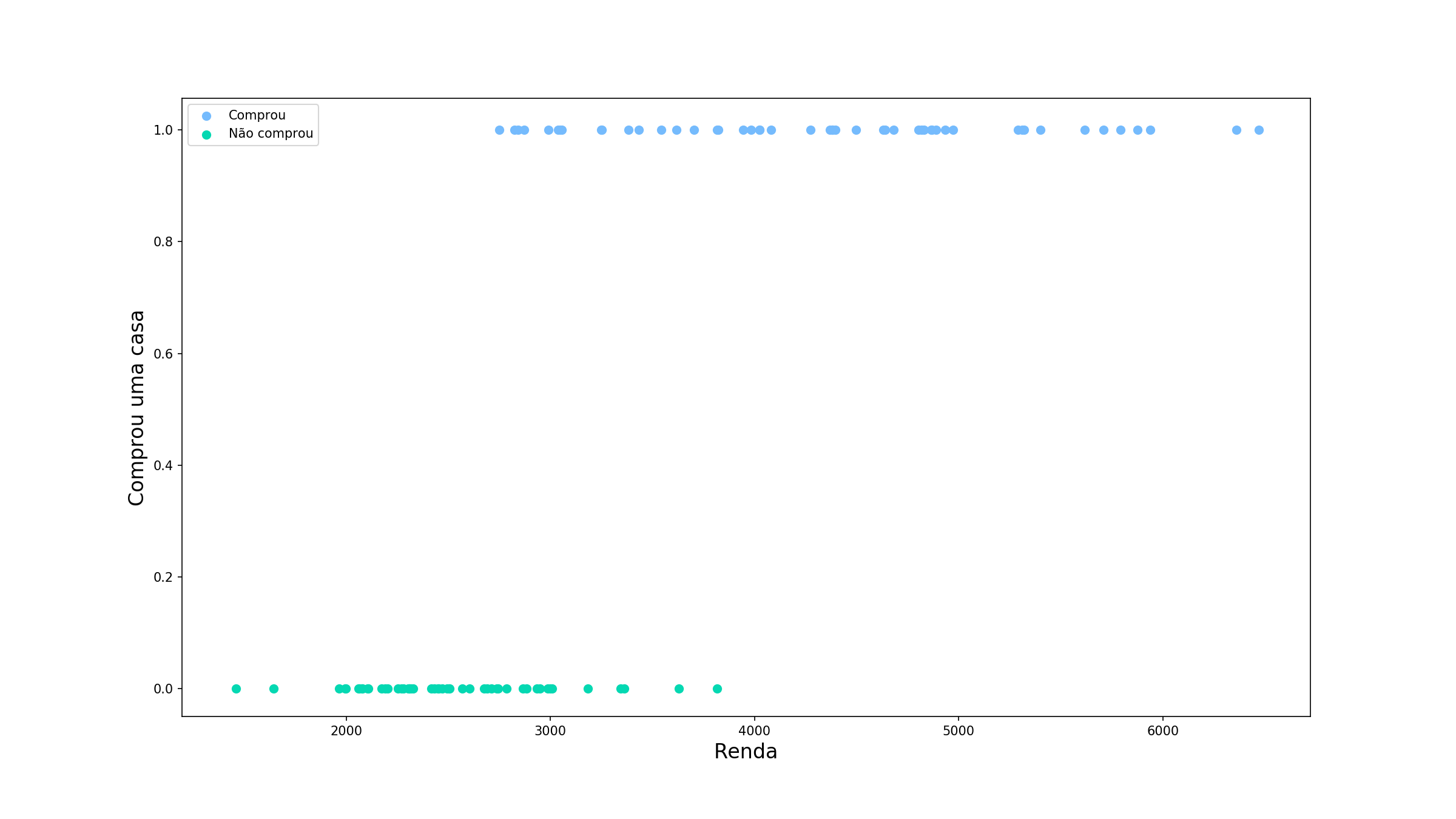
Agora estamos tentando prever se uma pessoa compraria uma casa em determinada região baseado na sua renda. Perceba que nossa variável alvo é limitada agora entre 0 (não comprou) e 1 (comprou). Vamos ver como nosso modelo anterior funcionaria.

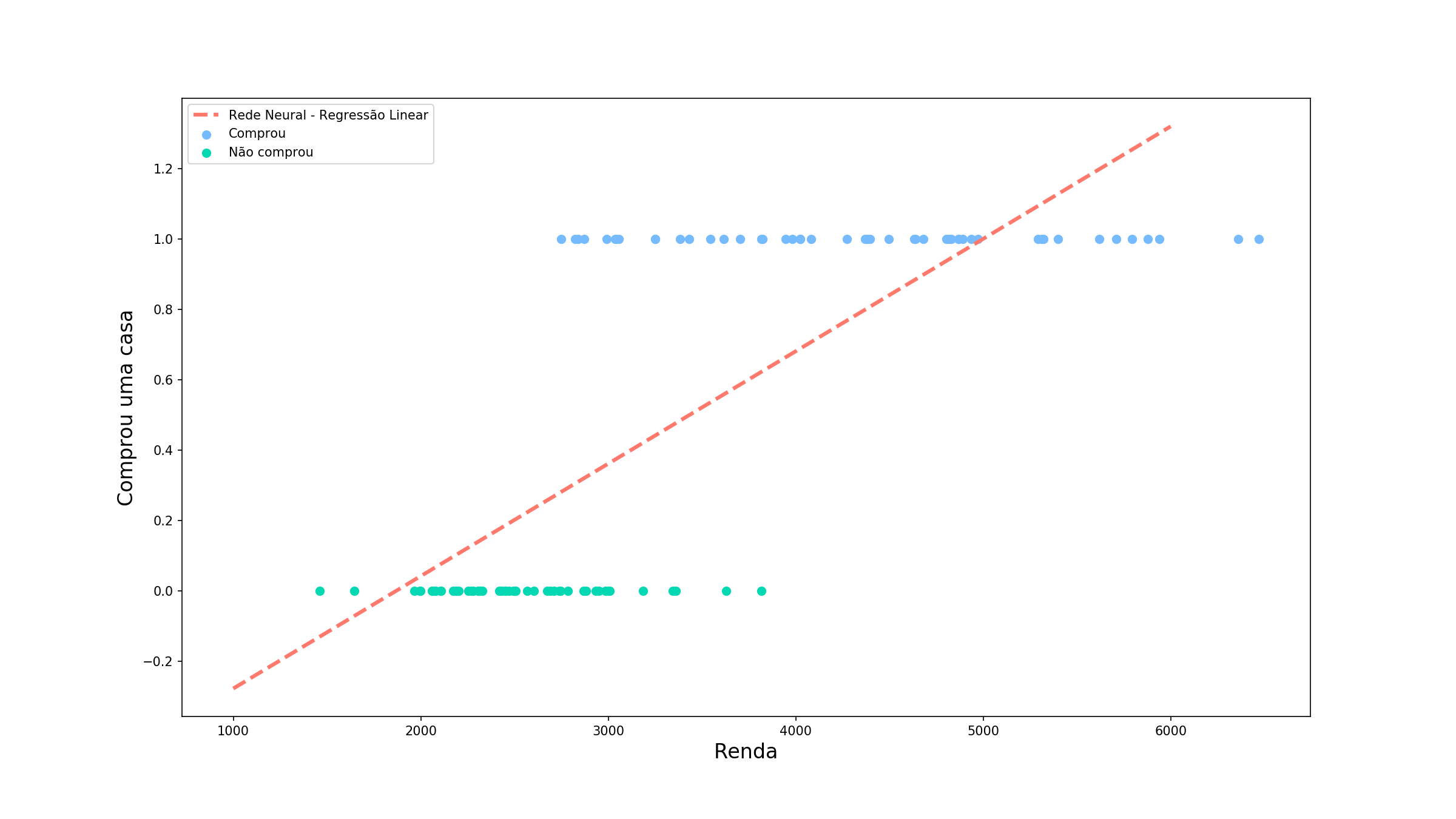
Não ficou muito legal, não é? Alguns valores de previsão ficaram abaixo de 0 e outros acima de 1 (o que isso significa???). Para o nosso problema esses valores não tem sentido algum, mas somente com uma combinação linear dos nosso valores de entrada, nós não temos como controlar quais os valores limites que a previsão pode assumir. É ai que entra o primeiro motivo para usarmos uma função de ativação:

Na camada de saída, a função de ativação é utilizada para mapearmos a saída da combinação linear dos neurônios dessa camada para o domínio esperado

Como nossos valores esperados estão entre 0 e 1, podemos por exemplo utilizar uma função chamada sigmóide para mapear a saída. A sigmóide tem a seguinte equação:

\[\large \sigma(x) = \frac{1}{1 + e^{-x}}\]

Vamos analisá-la com calma agora: quando x é muito grande, vamos dizer $\infty$, $e^{-x}$ tende a 0 e, assim, $\sigma(x)$ tende a 1. Em contrapartida, se x é muito pequeno, como $-\infty$, $e^{-x}$ tende a $\infty$ e como consequência $\sigma(x)$ tende a 0. Desse modo, conseguimos limitar a nossa saída para o domínio desejado. Mas espere! Essa função também já não é conhecida? Novamente você está certo: quando aplicamos a sigmóide na saída da combinação linear temos a mesma equação da Regressão Logística.

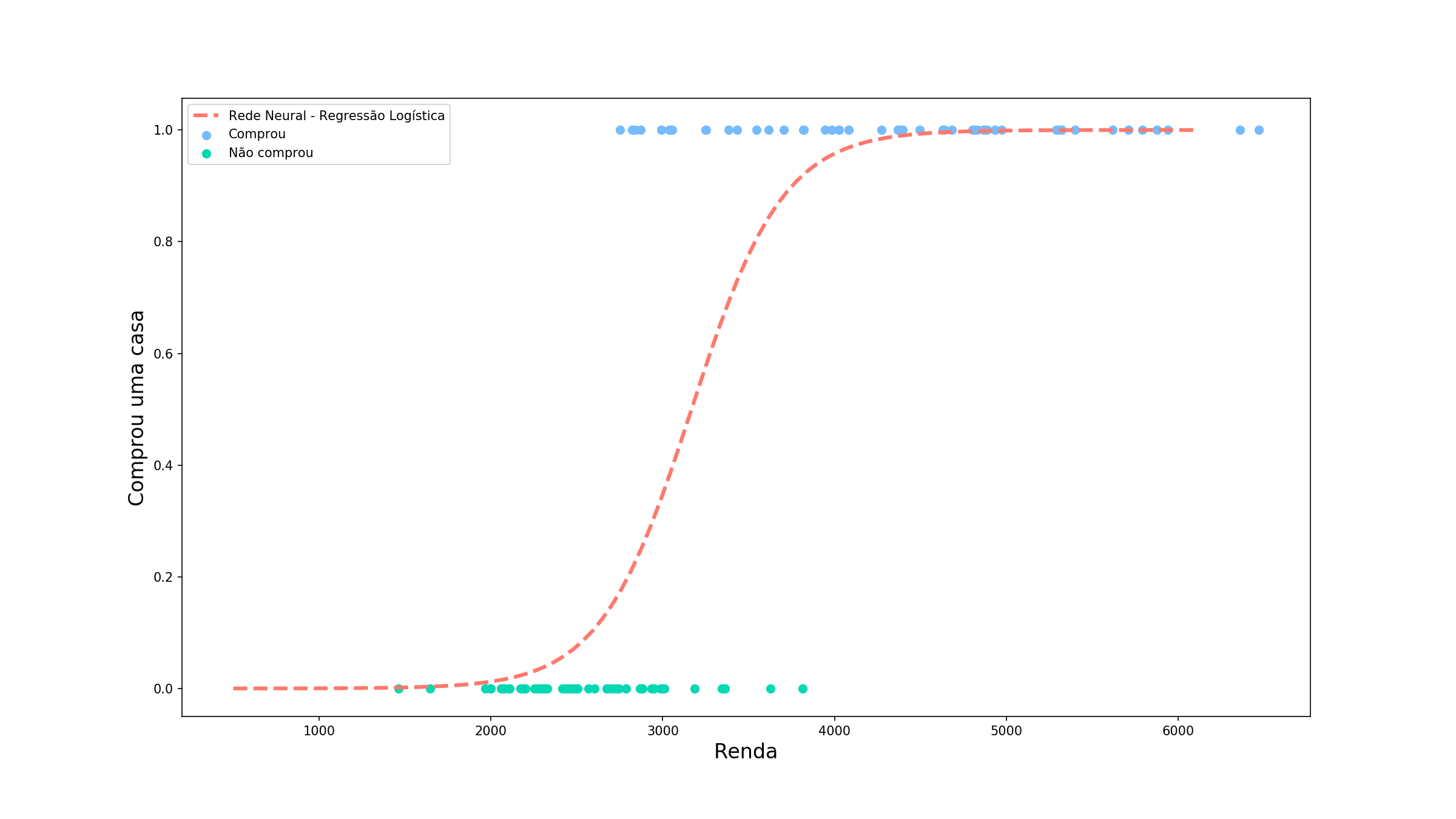
Vamos observar isso funcionaria no nosso diagrama da rede. Novamente vamos supor que ela já está treinada (vamos chegar lá, mais um pouco de paciência). Dessa vez, vamos tentar prever se um pessoa com renda de 6100 reais compraria uma casa nessa região.

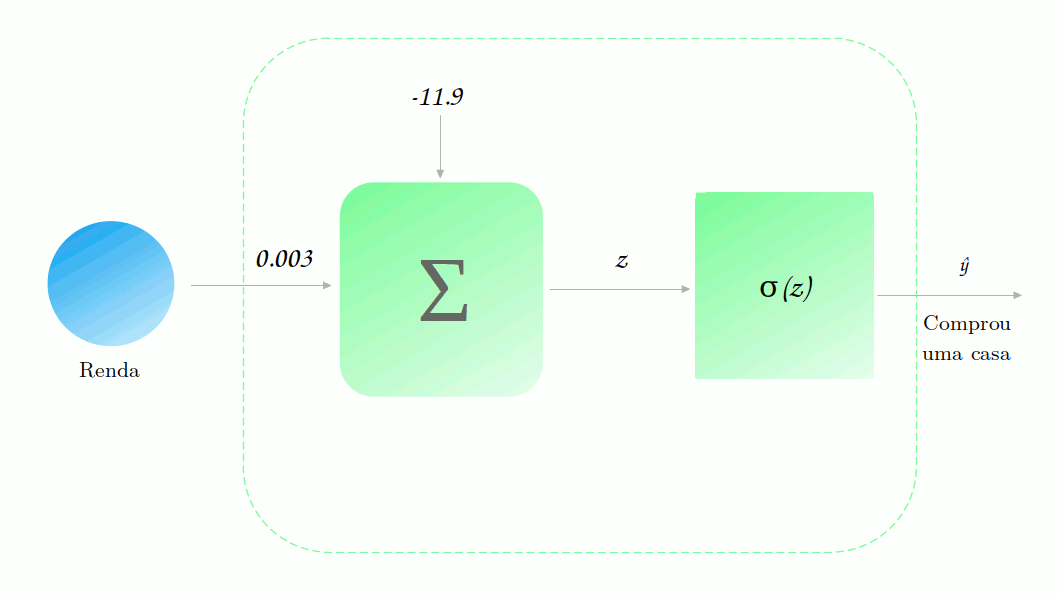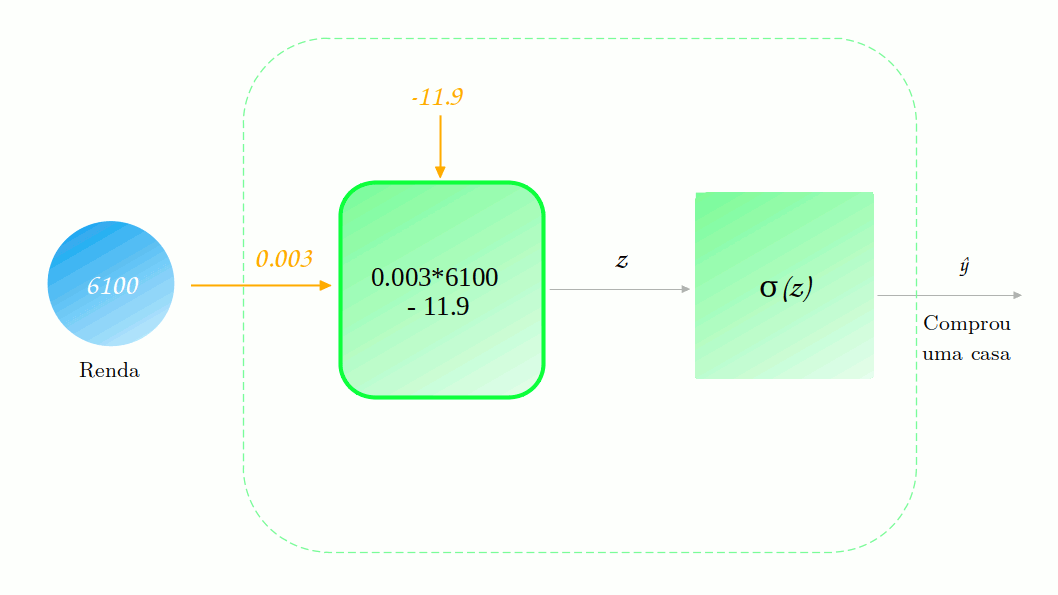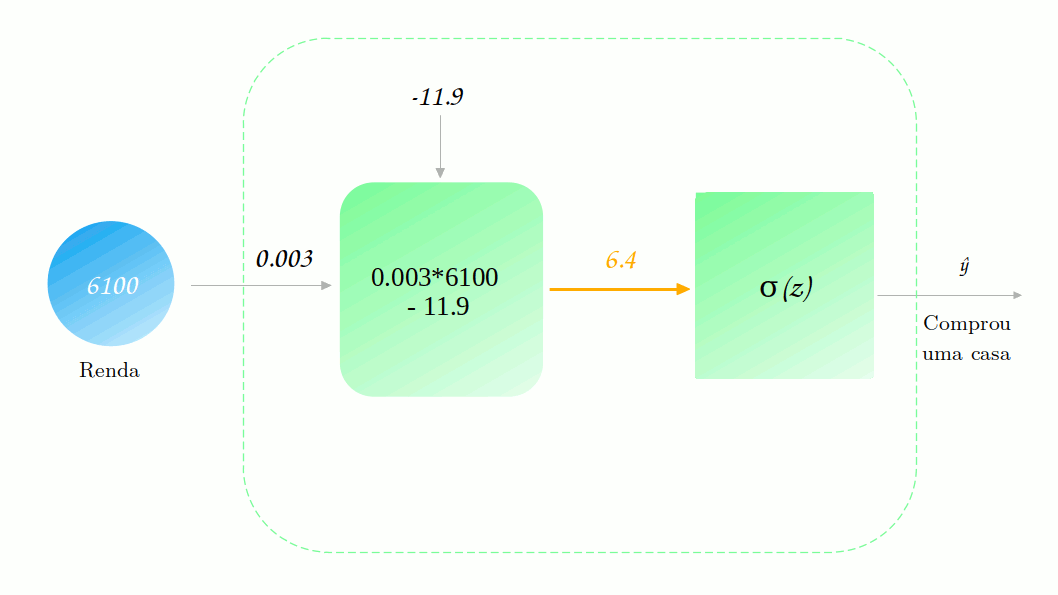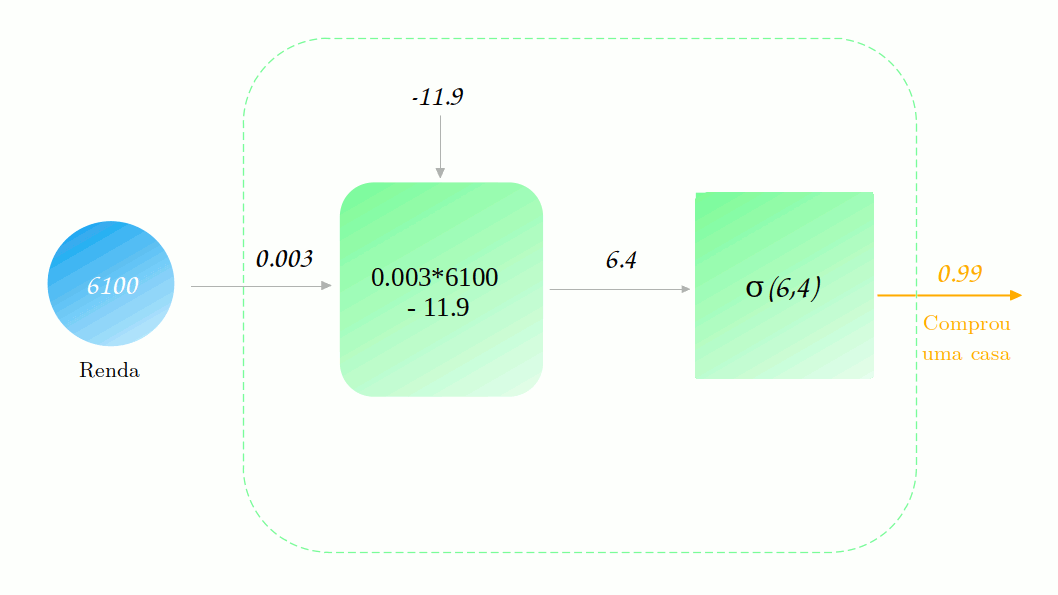
Podemos perceber que mesmo a saída da combinação linear sendo maior do que 1, a saída final do modelo é menor, como esperávamos que fosse. Esse comportamento se mantém para os outros de renda também. Agora não temos mais o problema de ter previsões que não fazem sentido!

Adicionando camadas

Vimos até agora uma arquitura básica de redes neurais, na qual não existia nenhuma camada oculta. Entretanto o grande poder das redes neurais vem das camadas ocultas. Já vamos entender o porquê disso, mas antes vamos introduzir algumas notações:

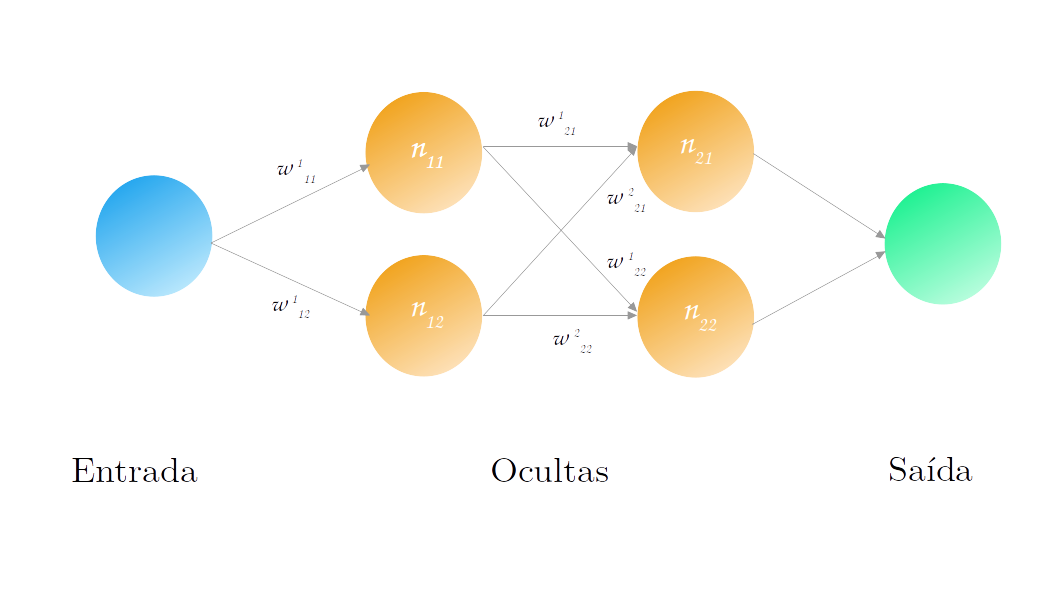
Utilizando essa notação, vamos escrever as equações da nossa rede na forma matricial (é só uma forma diferente de escrever que vai facilitar nossa vida daqui pra frente).

\[X_i = \begin{bmatrix} x_{i1}\\ \vdots\\ x_{ik} \end{bmatrix} \in \mathbb{R}^{k\times 1}\] \[O_i = \begin{bmatrix} o_{i1}\\ \vdots\\ o_{ij} \end{bmatrix} \in \mathbb{R}^{j\times 1}\] \[W_i = \begin{bmatrix} w_{i1}^1 & \cdots & w_{ij}^1 \\ \vdots & \ddots & \vdots \\ w_{i1}^k& \cdots & w_{ij}^k \end{bmatrix} \in \mathbb{R}^{k \times j}\]

Assim, a equação que mapeia a entrada $X_i$ para a saída $O_i$ é:

\[O_i = f(W_i^T X_i + b_i),\]

em que $b_i \in \mathbb{R}^{j\times 1}$ é um vetor com os bias de cada neurônio da camada.

O poder das funções de ativação

Na camada de saída já vimos que a função de ativação é importante para limitarmos o domínio da saída para coincidir com o domínio esperado. Mas existe uma outra utilidade que talvez seja a mais importante. Vamos supor que no nosso exemplo com duas camada ocultas e dois neurônios em cada não utilizamos nenhuma função de ativação.

Na primeira camada temos:

\[\large O_1 = W_1^T X_1+ b_1\]

Já na segunda camada, a saída da camada anterior é a nossa entrada, então:

\[\large O_2 = W_2^T O_1+ b_2\] \[\large O_2 = W_2^T (W_1^T X_1 + b_1)+ b_2\] \[\large O_2 = (W_2^T W_1^T) X_1 + (W_2^T b_1 + b_2)\] \[\large O_2 = W^{\prime T}_2 X_1 + b^\prime_2\]

Calma ai! O que é esse monte de equação?? Podem ficar tranquilos, apesar de parecer complicado o que queremos mostrar é muito simples: se não utilizarmos uma função de ativação, a saídas das camadas mais profundas serão apenas combinações lineares da entrada. É como se estivessemos fazendo cálculos extras para chegar na mesma reposta. Tendo isso em mente, a segunda característica importante das funções de ativação é:

A funções de ativação introduzem não-linearidades nas camadas intermediárias que diminuem o viés do modelo como um todo. Caso elas não existissem, só conseguiríamos modelar, até a camada de saída, funções lineares.

E agora?

Hoje vimos quais elementos compõem uma rede neural, qual a importância de cada um e como eles são utilizados para realizar previsões. Parabéns por ter chegado até aqui! Já temos uma visão geral do funcionamento de um rede treinada, mas fica a questão: como a rede aprende quais são os melhores parâmetros? Esse será o tema do próximo artigo da série: Ensinando Redes Neurais. Não perca!