10 min de leitura
Ensinado Redes Neurais

Fala, pessoal! Bem-vindos de volta! Espero que tenham gostado do último artigo em que apresentamos os conceitos básicos de redes neurais. Até o momento, sempre que passávamos por uma iteração da rede dizíamos que os pesos já estavam treinados, mas nunca comentamos como os pesos foram treinados. Chegou a hora! Vamos falar de como podemos ajustar os pesos para que tenhamos previsões cada vez melhores.
O Gradiente
Para introduzirmos esse assunto, precisamos lembrar de um conceito de cálculo: o gradiente. Em termos matemáticos, podemos escrever o gradiente da seguinte maneira:
\[\nabla f(x_1, \cdots, x_n) = \begin{bmatrix} \frac{\partial f}{\partial x_1}\\ \vdots\\ \frac{\partial f}{\partial x_n} \end{bmatrix} \in \mathbb{R}^{n\times 1}\]mas isso não quer dizer muita coisa. Para entendermos como ele é utilizado para ensinar as redes, precisamos entender um pouco de sua intuição geométrica.
O vetor gradiente de uma função $f$ indica a direção em que o valor da função cresce de maneira mais rápida.
Ok … ainda não entendi. Sem problemas, vamos utilizar um exemplo mais prático. Suponha que queremos encontrar o valor máximo da função $f(x) = -x^2$ ($f$ só depende de uma variável, mas para efeitos didáticos fica mais fácil de ensinar). Graficamente, ela tem o seguinte formato.
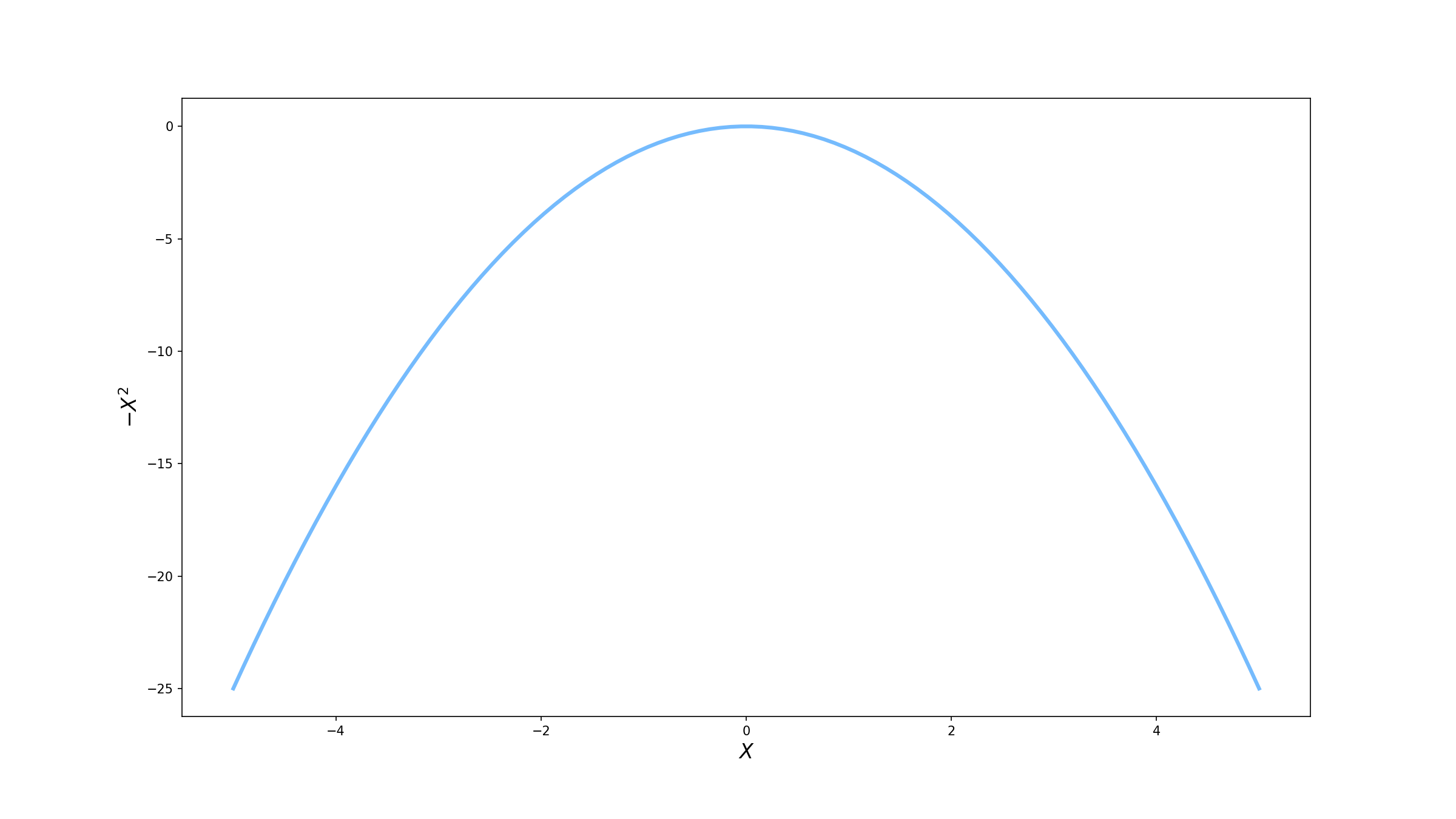
Vamos supor também que já estamos em cima dessa curva, no ponto $x=-4$. Como $f$ tem dependência somente na variável $x$, temos duas opções: ou adicionamos um valor positivo em $x$ e “andamos” para a direita, ou adicionamos um valor negativo e vamos para a esquerda.
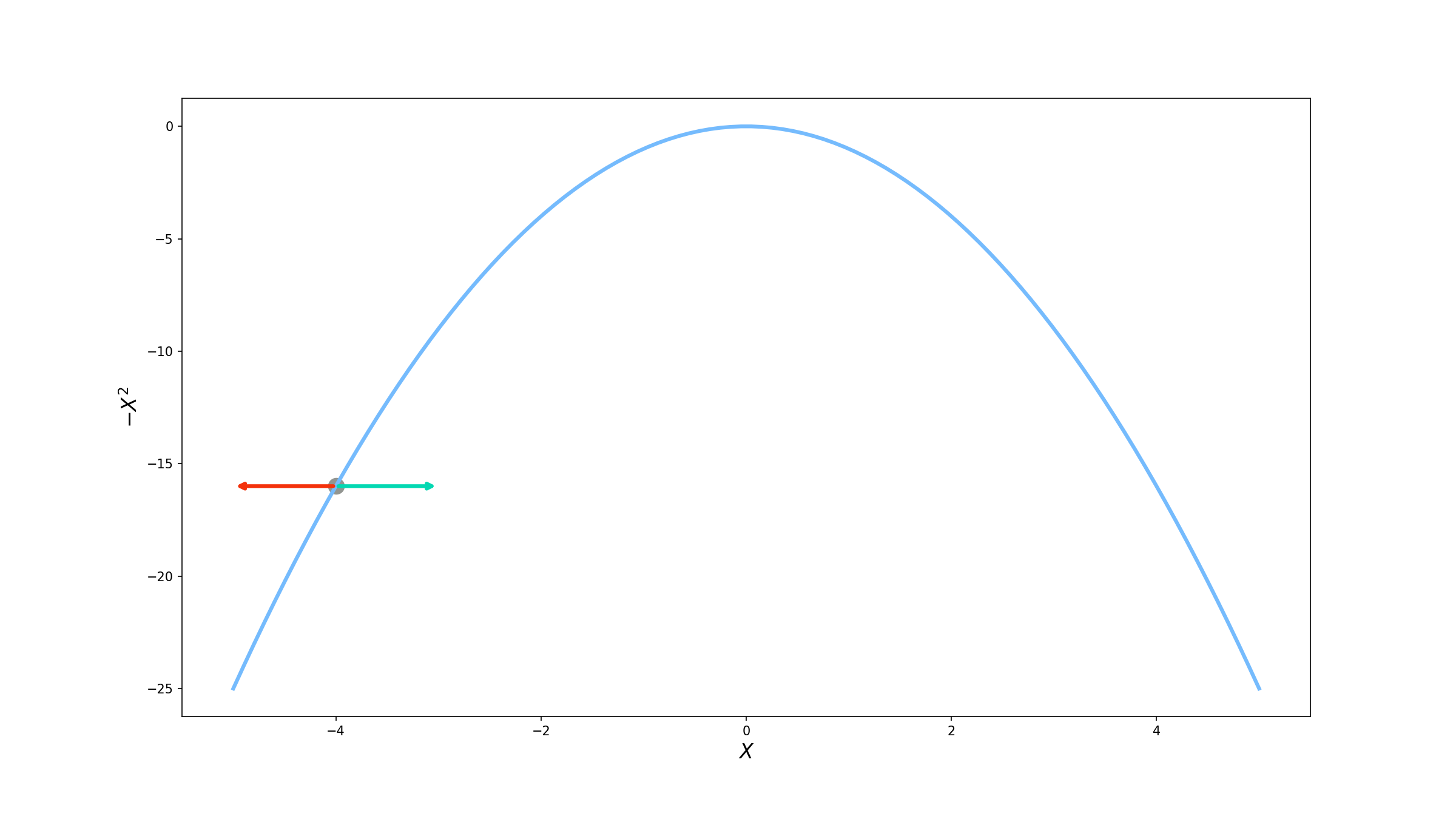
Visualmente, podemos ver que devemos ir para a direita, mas como podemos ter certeza pensando matematicamente? É ai que entra o gradiente! Como falamos o gradiente indica a direção de maior crescimento da função. Vamos começar calculando então o vetor gradiente.
\[\nabla f(x) = \begin{bmatrix} \frac{\partial f}{\partial x} \end{bmatrix} = \begin{bmatrix} -2x \end{bmatrix}\]Vamos com calma agora. Dissemos que o vetor nos daria uma direção, mas pelo que calculamos ainda temos uma função de $x$. Isso é devido ao fato de para cada $x$ termos uma valor diferente de gradiente o que leva a uma direção diferente também. Para sabermos qual a direção no ponto em que estamos, basta substituirmos o valor do ponto atual no gradiente. Assim,
\[\nabla f(-4) = \begin{bmatrix} -2x \end{bmatrix} = \begin{bmatrix} 8 \end{bmatrix}\]Ótimo! Calculamos o nosso gradiente, vimos que ele é positivo e então temos que "andar" para a direita, como esperávamos. Mas quanto devemos andar? Vamos tentar dar um passo da magnitude do gradiente:
\[|\nabla f(-4)| = 8\]Com isso vamos parar em $x=4$ .
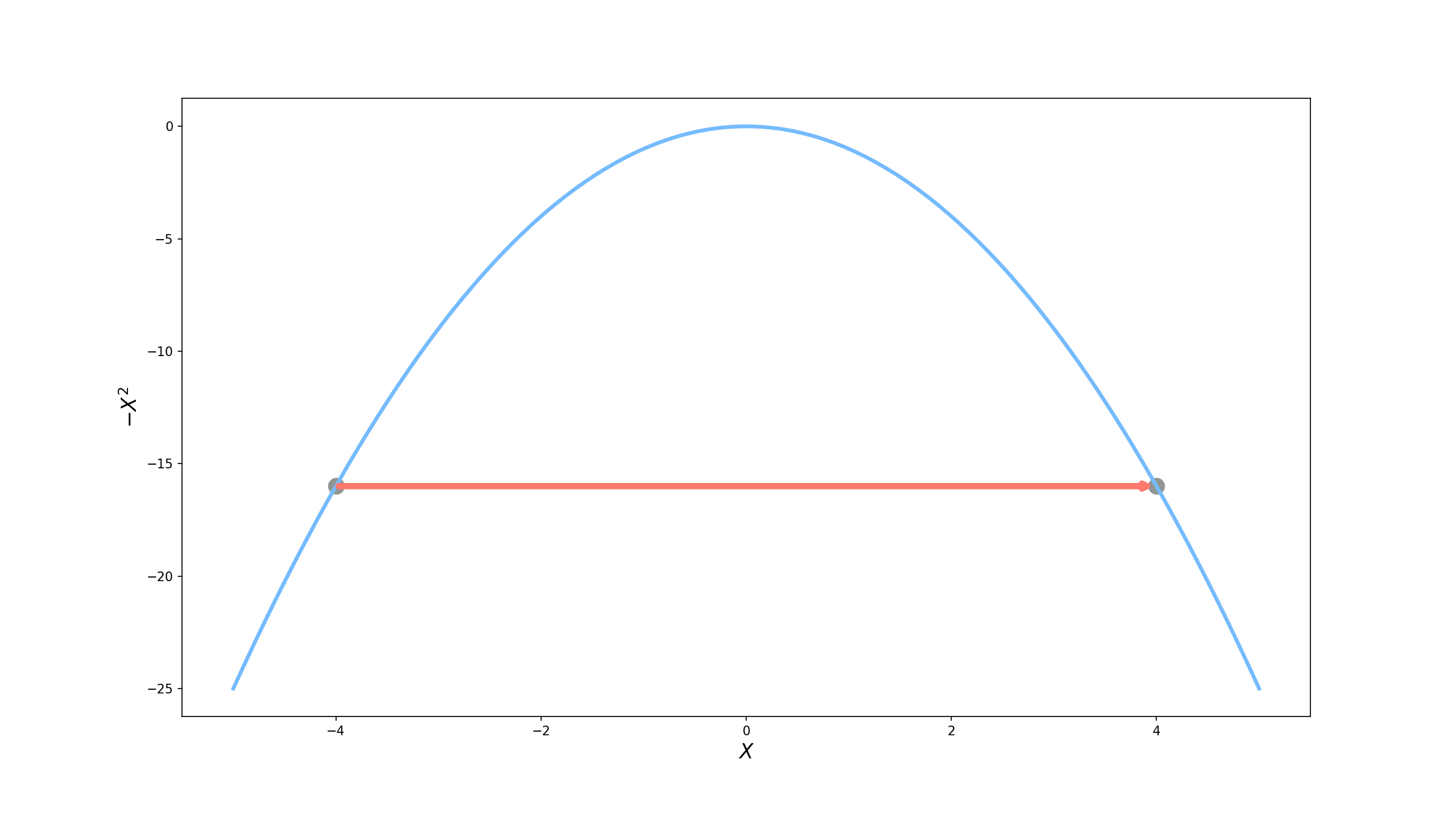
Hum... Não parece que melhorou muito. Ainda estamos com um valor $f(4)=16$, o mesmo que na posição anterior. E se calcularmos o gradiente de novo?
\[\nabla f(4) = \begin{bmatrix} -2x \end{bmatrix} = \begin{bmatrix} -8 \end{bmatrix}\]Dessa vez o gradiente é negativo, logo temos que ir para a esquerda. Porém se dermos de novo um "passo" da magnitude do vetor gradiente, voltaríamos para $x=-4$, a nossa posição inicial. Parece que esse método não está levando a nenhum lugar, não é? Vamos tentar então uma outra abordagem. Ao invés da darmos um passo com a magnitude total do gradiente, vamos utilizar só uma porcentagem desse valor. Para testar, vamos fazer $10\%$.
\[x^\prime = x + 0.1*|\nabla f(x)| = -4 + 0.1 * 8 = -3.2\]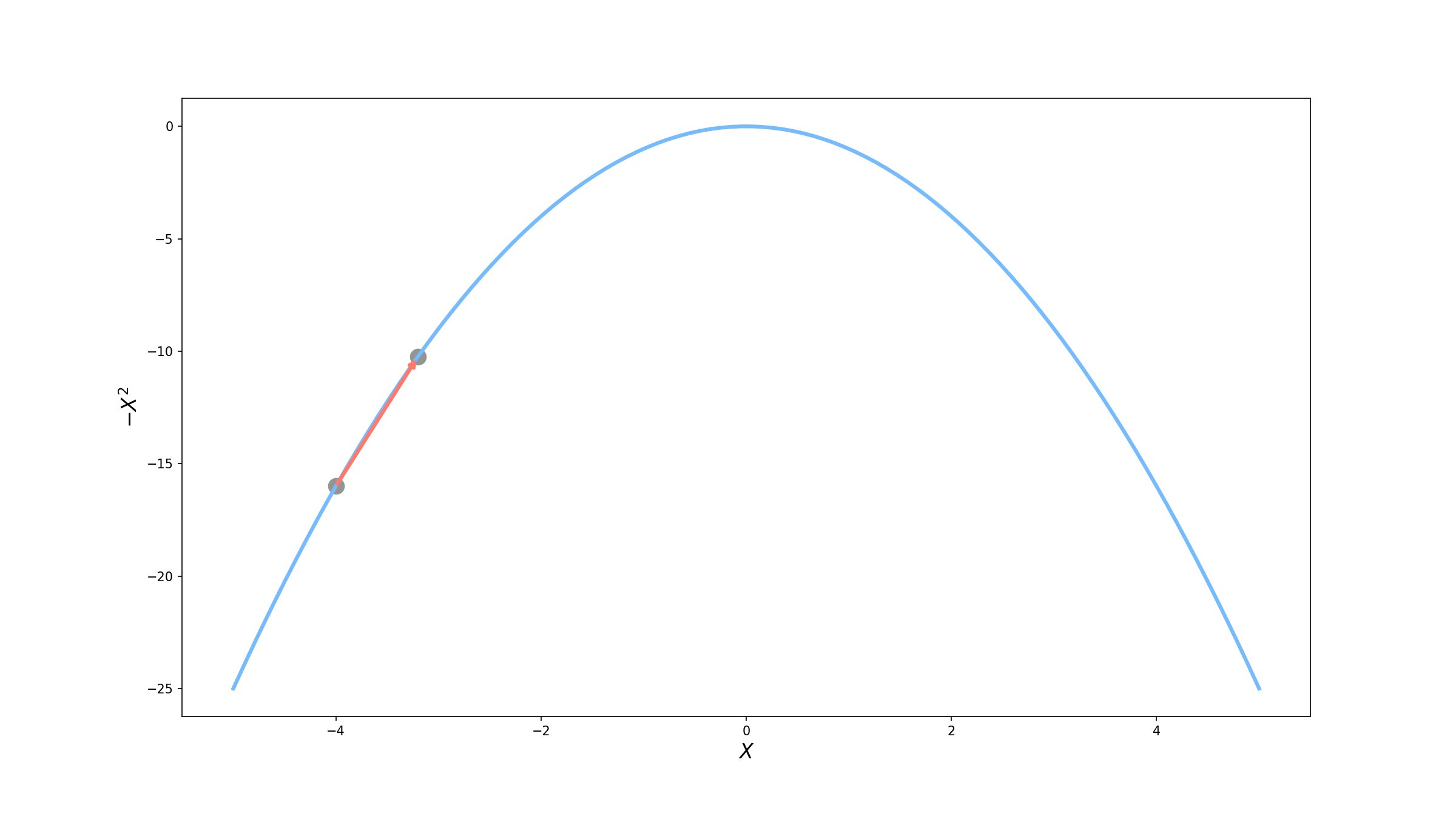
Uou! Dessa vez conseguimos aumentar o valor da nossa função para $f(-3.2) = -10.24$. Parece promissor, mas vamos tentar mais uma vez.
\[x^\prime = x + 0.1*|\nabla f(x)| = -3.2 + 0.1* 6.4 = -2.56\]Ainda melhor! Agora temos $f(-2.56) = -6.55$.
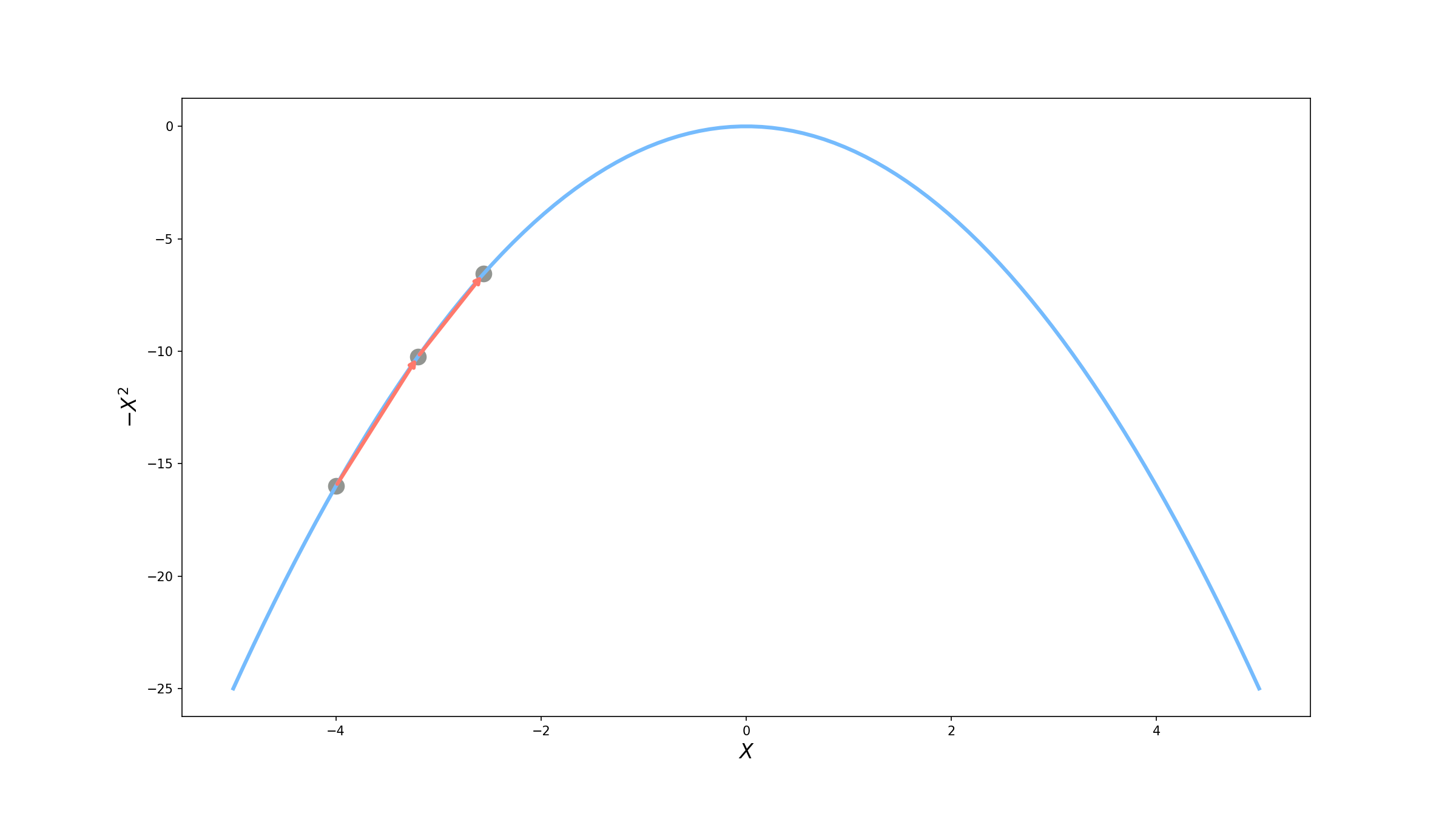
Parece que essa abordagem de utilizar uma porcentagem da magnitude do gradiente funcionou muito bem e é exatamente essa técnica que vamos utilizar. Na verdade, essa porcentagem que utilizamos tem um nome muito especial: taxa de aprendizagem e a referenciamos pela letra grega $\alpha$. É ela quem controla o tamanho do passo que damos. Pudemos ver que se o passo for muito longo, como quando utilizamos o valor 1 ($100\%$), podemos nunca aumentar o valor ou, pior ainda, diminuí-lo. Mas e se a taxa de aprendizagem for muito pequena? Nesse caso não temos problema com a convergência, mas sim o tempo que leva para a atingirmos. Vamos supor que agora $\alpha = 0.01$ ou seja $1\%$.
\[x_1 = x_0 + 0.01*|\nabla f(x_0)| = -4 + 0.01*8 = -3.92\] \[x_2 = x_1 + 0.01*|\nabla f(x_1)| = -3.92 + 0.01* 8 = -3.84\]Veja que depois de duas iterações, atingimos o valor de $f(-3.84) = -14.75$, enquanto antes tinhamos $f(-2.56) = -6.55$. Podemos ver que a escolha da taxa de aprendizagem não é trivial:
Se $\alpha$ for muito grande corremos o risco de não convergir para o máximo e se for muito pequena podemos demorar muito para atingí-lo.
Função de perda
A utilização do gradiente é ótima para otimizarmos funções, mas que função nós estamos querendo otimizar quando falamos de redes neurais? Para tangibilizar, vamos tratar especificamente da rede mais simples vimos até agora: a regressão linear. Vamos até utilizar nosso exemplo anterior de previsão do peso em função da altura.
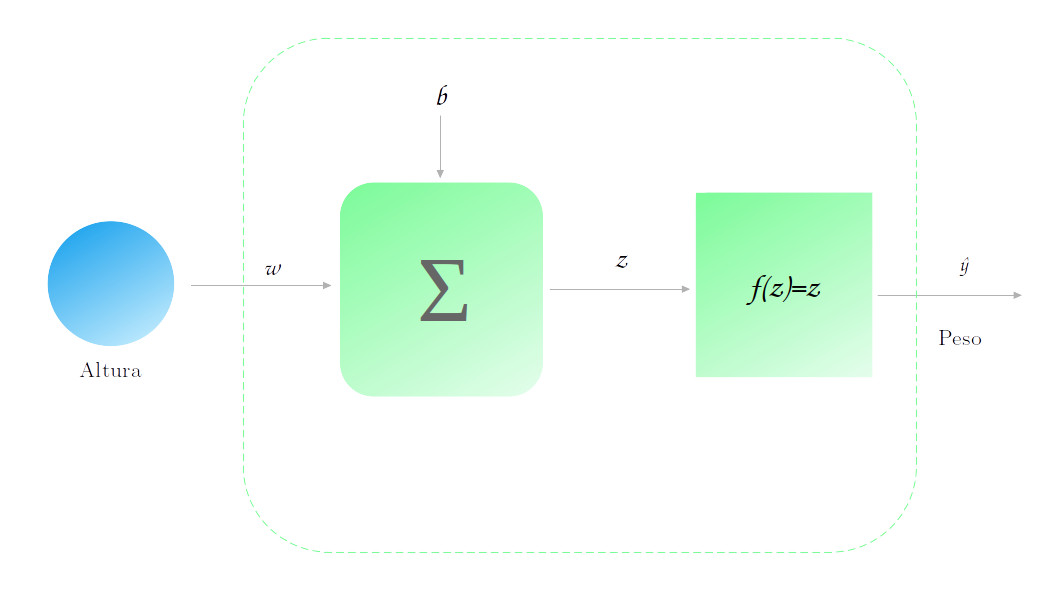
Inicialmente nem nosso parâmetro $w$ nem nosso parâmetro $b$ estão treinados. Geralmente, eles são iniciados com um valor aletório, vamos dizer $w=0.7$ e $b=6$. A curva de previsão da nossa rede é então:
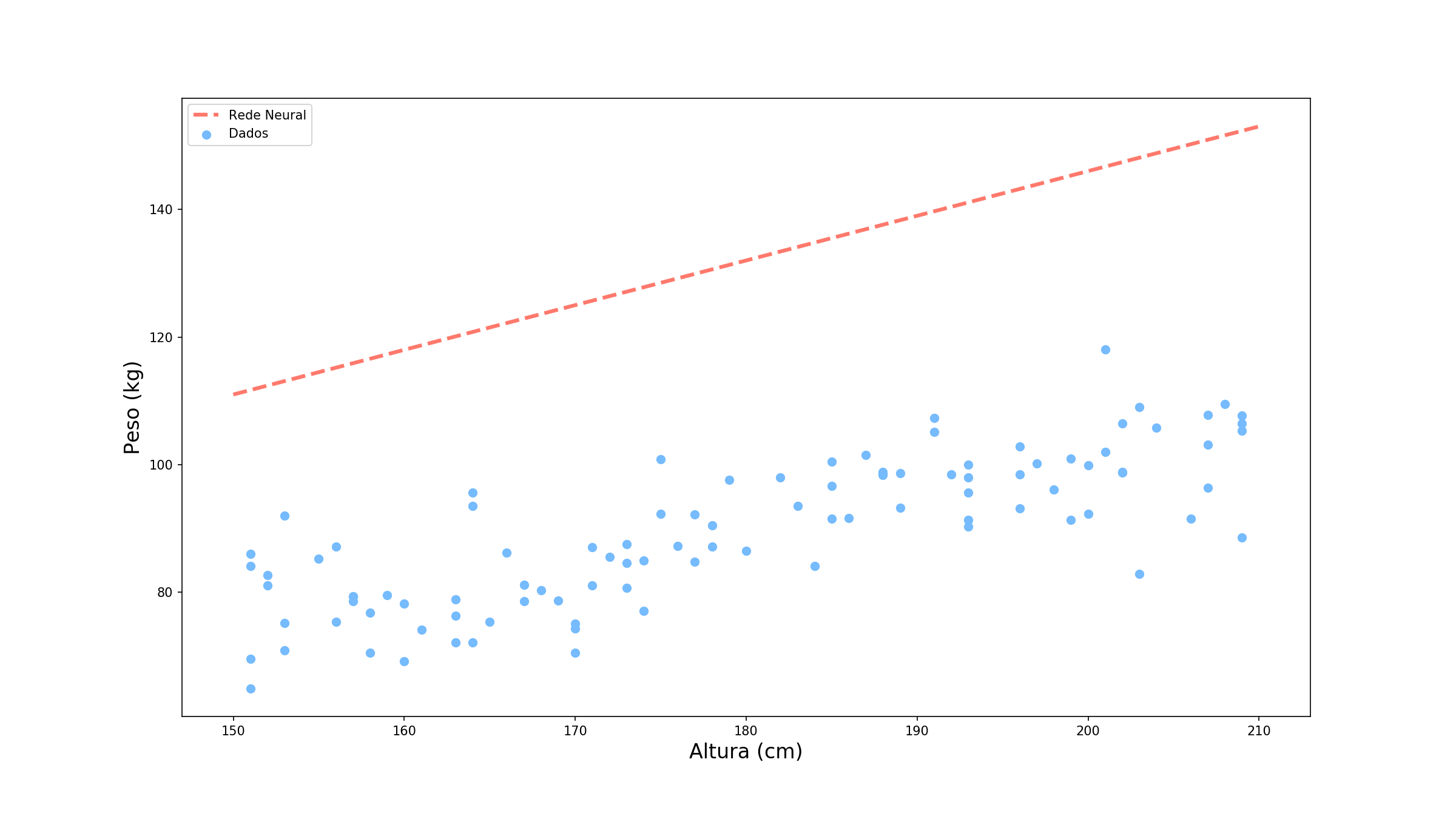
Não está muito legal, não é? Mas quão ruim ela está? Vamos tomar o exemplo de um ponto específico Altura = 177cm (você já viu esse ponto em algum lugar?). Vamos observar como é dada a previsão para esse ponto.
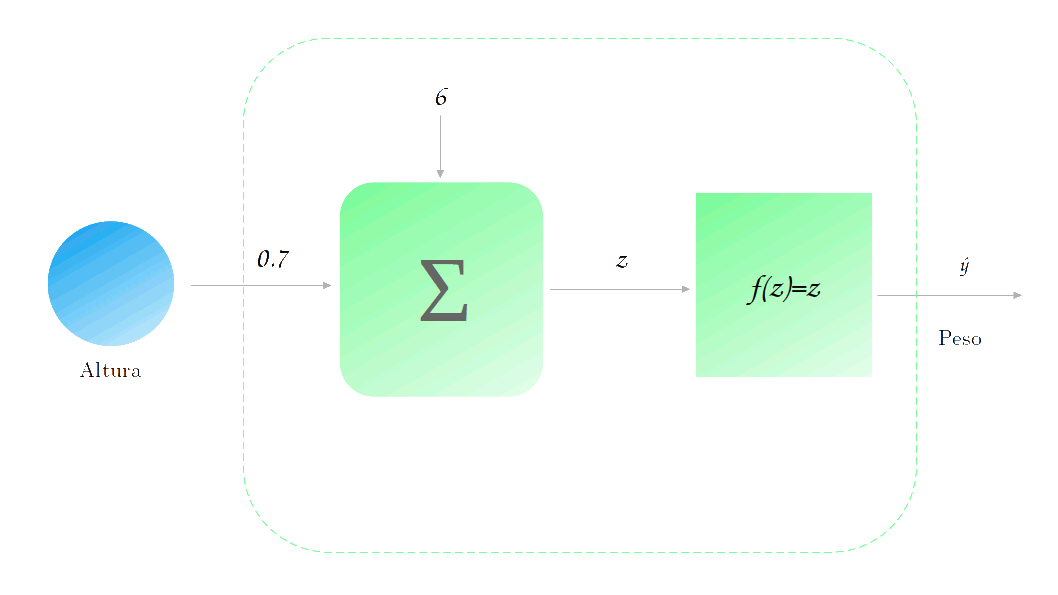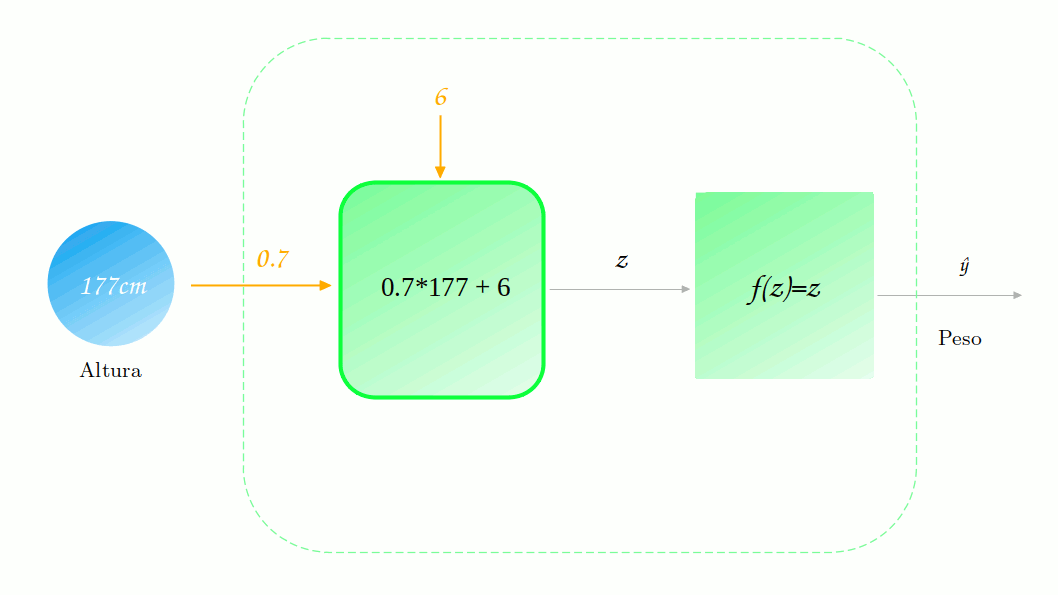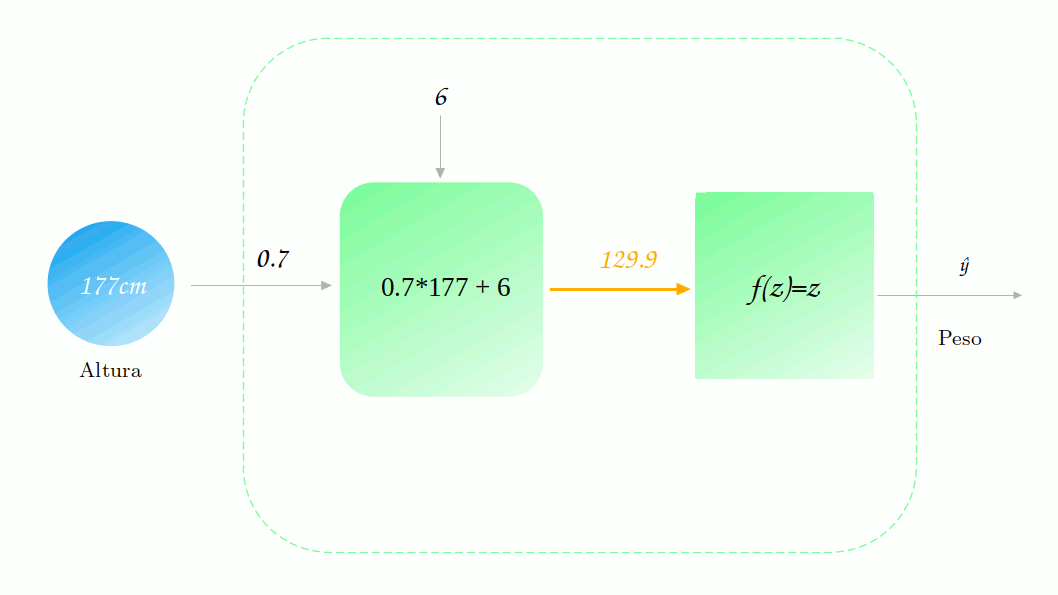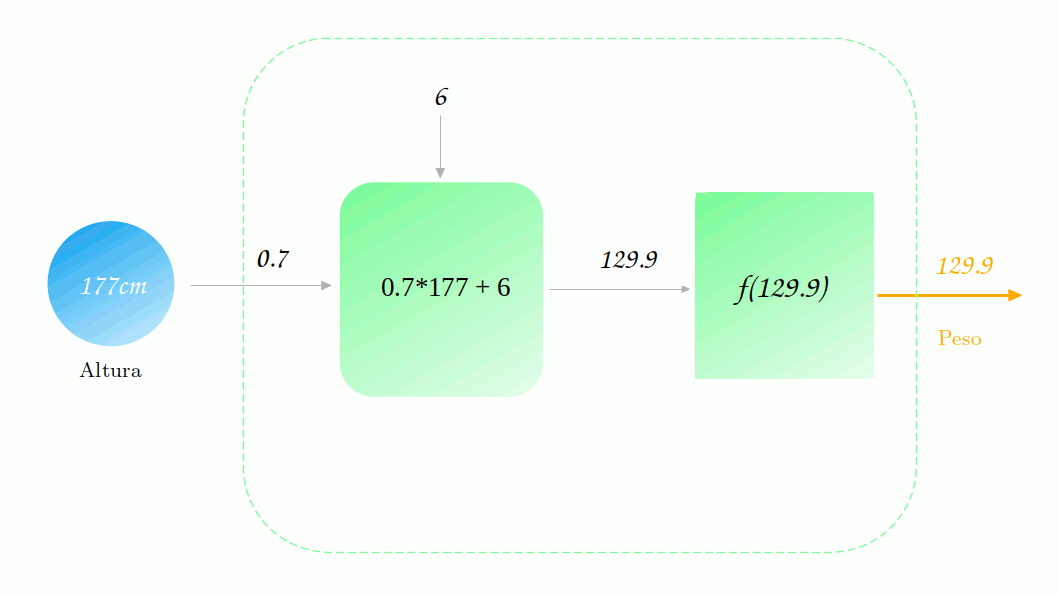
Vamos supor que o valor correto para essa altura é de 88.2. Sendo assim, o quão distante nossa previsão de 129.9 está do valor real? Para responder a essa pergunta precisamo definir uma função de perda (loss functions). Para mantermos os cálculos simples, vamos utilizar uma função muito comum: o erro quadrático.
\[\mathscr{L}(y, ŷ) = \frac{1}{2} (ŷ-y)^2,\]em que $y$ é o valor observado e $ŷ$ é o valor previsto. Um ponto interessante dessa função é que queremos minimizá-la ao invés de maximizá-la como fizemos anteriormente, afinal queremos ter uma diferença cada vez menor entre a resposta real e o valor previsto. Isso significa que não podemos utilizar o gradiente? De jeito nenhum! Ainda podemos (e vamos) utilizá-lo mas com uma pequena modificação:
Quando queremos minimizar uma função não utilizamos a direção do gradiente e sim a direção inversa. Isso nos indica em qual direção a função tende a diminuir mais rápido.
Podemos pensar que quando queremos maximar uma função estamos escalando-a na direção do gradiente e quando queremos minimizá-la estamos descendo. É por esse motivo que chamamos esse algoritmo de gradiente descendente.
Vamos tentar agora atualizar nossos parâmetros. No nosso modelo temos 2 parâmetros que precisam ser treinados: $w$ e $b$. Vamos começar com $w$:
\[ŷ = w * x + b\]Logo,
\[\frac{\partial \mathscr{L}}{\partial w} = \frac{\partial \mathscr{L}}{\partial ŷ} \frac{\partial ŷ}{\partial w}\]Aqui utilizamos outro conceito de cálculo: a regra da cadeia. Vamos calcular essas duas derivadas separadamente:
\[\frac{\partial \mathscr{L}}{\partial ŷ} = ŷ-y\]e
\[\frac{\partial ŷ}{\partial w} = x\]Com isso, podemos combiná-las e chegaremos a:
\[\frac{\partial \mathscr{L}}{\partial w} = (ŷ-y)*x = (88.2-129.9)*177 = 7380.9\]Vamos então atualizar nosso peso $w$. A mudança que temos que fazer agora é que para utilizar a direção inversa do gradiente, em vez de somá-lo ao valor atual, vamos subtraí-lo.
\[w^\prime = w - \alpha * \frac{\partial \mathscr{L}}{\partial w}\]Vamos utilizar $\alpha=0.00005$ (como chegamos nesse valor é outro caso).
\[w^\prime = 0.7 - 0.00005 * 7380.9 = 0.7 - 0.36 = 0.34\]Legal! Já temos nosso novo valor para $w$. Se fizermos o mesmo procedimento para $b$, chegaremos na seguinte equação:
\[\frac{\partial \mathscr{L}}{\partial b} = (ŷ-y) = 129.9 - 88.2 = 41.7\]Para atualizarmos nosso parâmetro:
\[b^\prime = b - \alpha * \frac{\partial \mathscr{L}}{\partial b}\] \[b^\prime = 6 - 0.00005 * 41.7 = 6 - 0.002 = 5.998\]Ótimo! Agora temos nosso dois novos parâmetros. Vamos ver qual a nova previsão para esse modelo.
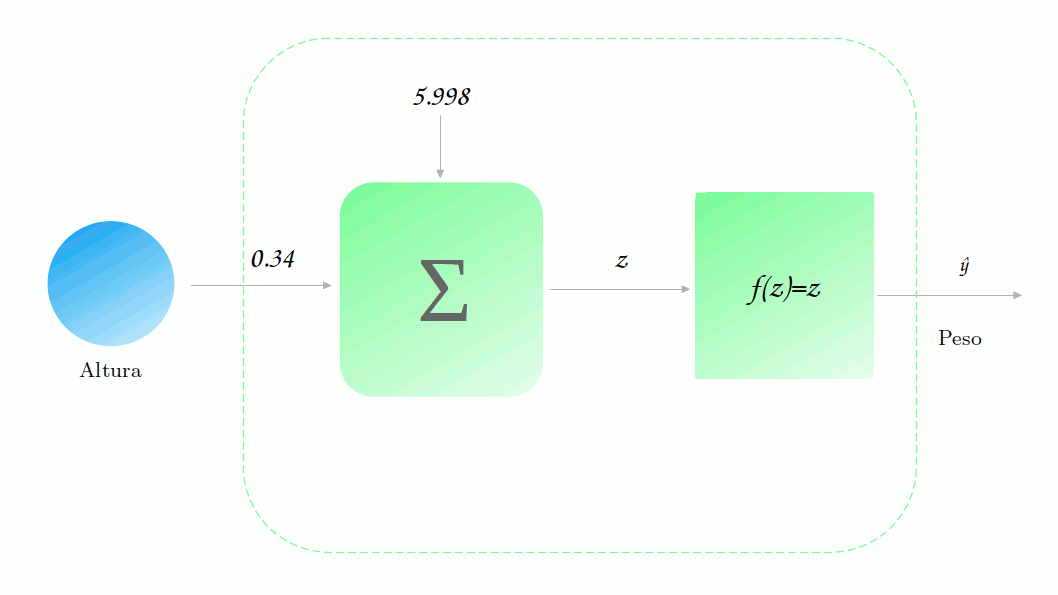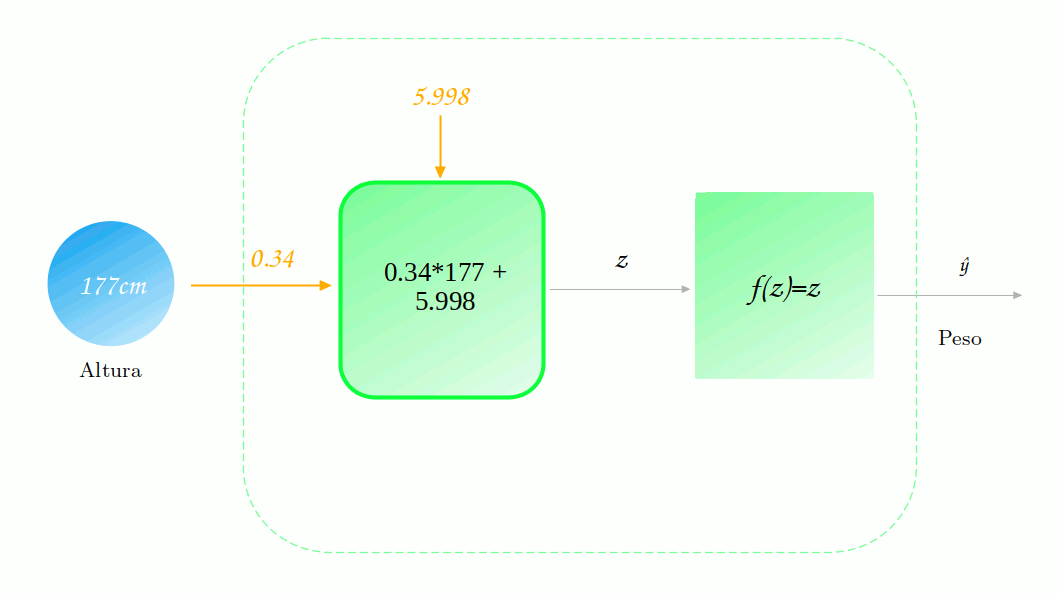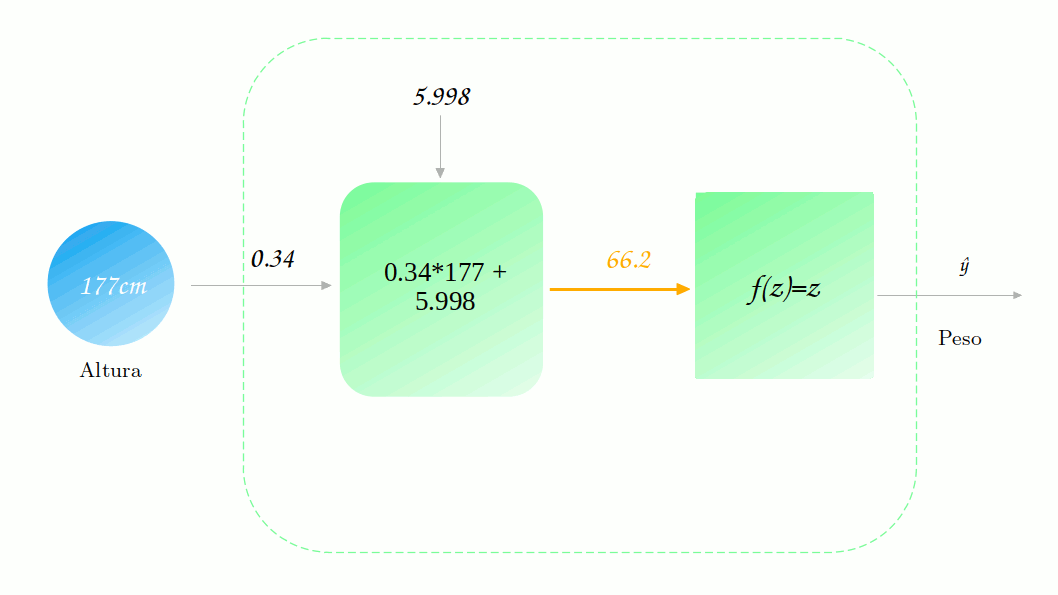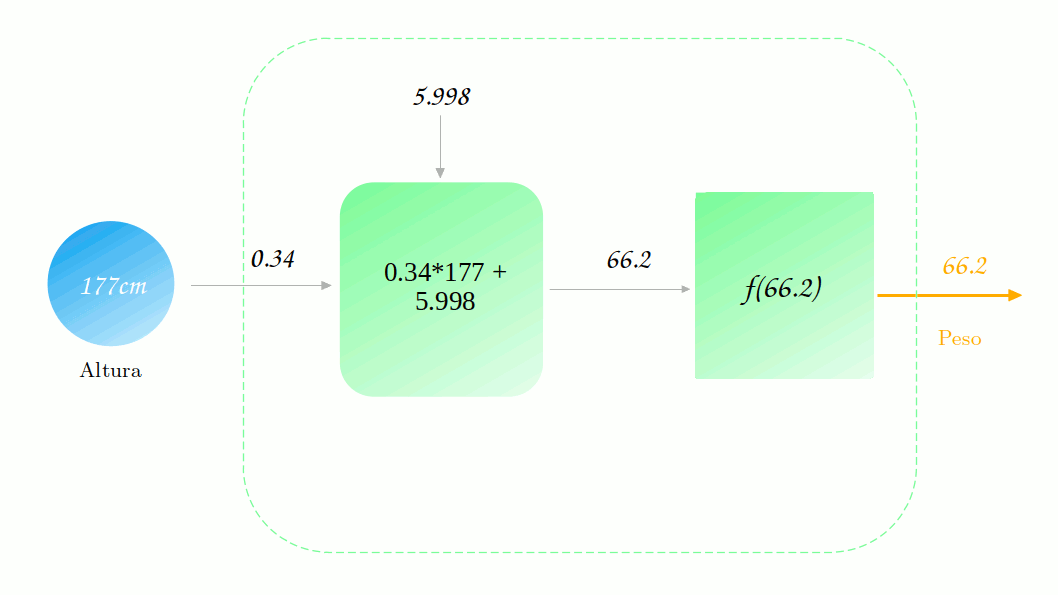
Mas será que o erro diminuiu mesmo? Vamos verificar.
\[\mathscr{L} (88.2, 129.9) = \frac{1}{2} (129.9-88.2)^2 = \frac{1}{2} 41.7^2 = 869.45\] \[\mathscr{L} (88.2, 66.2) = \frac{1}{2} (66.2-88.2)^2 = \frac{1}{2} 22^2 = 242\]Uau! Diminuimos muito o erro!
Função de custo
Um ponto importante da discussão anterior é que atualizamos os parâmetros da rede baseados somente na previsão para uma amostra. Na prática, nós olhamos mais que uma única amostra. Para fazer isso, nós definimos a chamada função de custo. Essa função de custo nada mais é do que a média dos erros para cada amostra.
\[\mathscr{C} = \frac{1}{n} \sum_{i=1}^n \mathscr{L}(y_i, ŷ_i)\]Se atualizarmos os pesos baseados na função de custo, o gradiente tem a ser mais estável evitando atualizações desnecessárias. A ideia do gradiente descendente é que continuemos a atualizar os pesos até termos um erro satisfatoriamente baixo ou até atingirmos um número de épocas (uma época é uma passada total por todas as amostras da base). Abaixo temos o treino do nosso exemplo para 10 épocas.
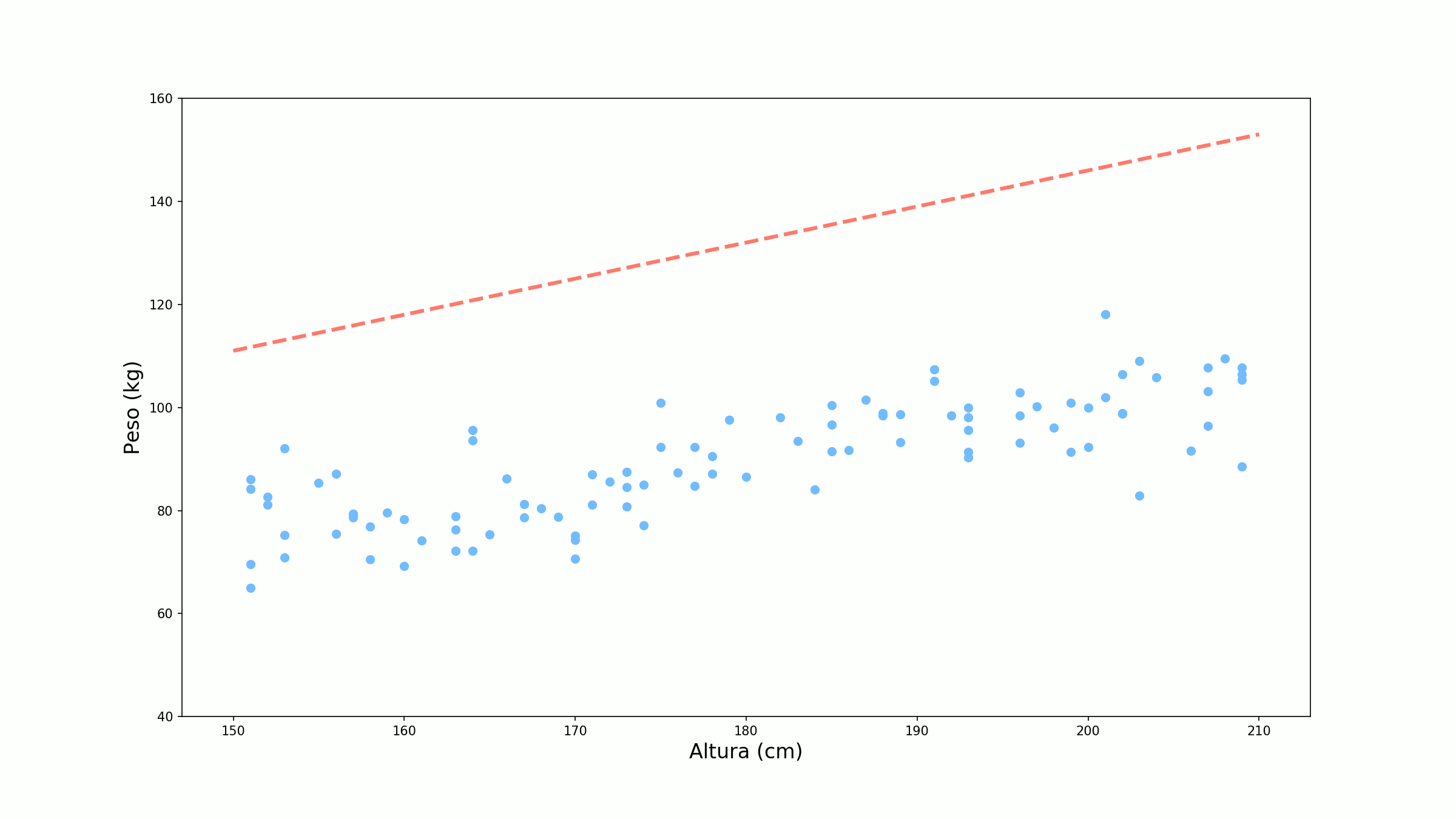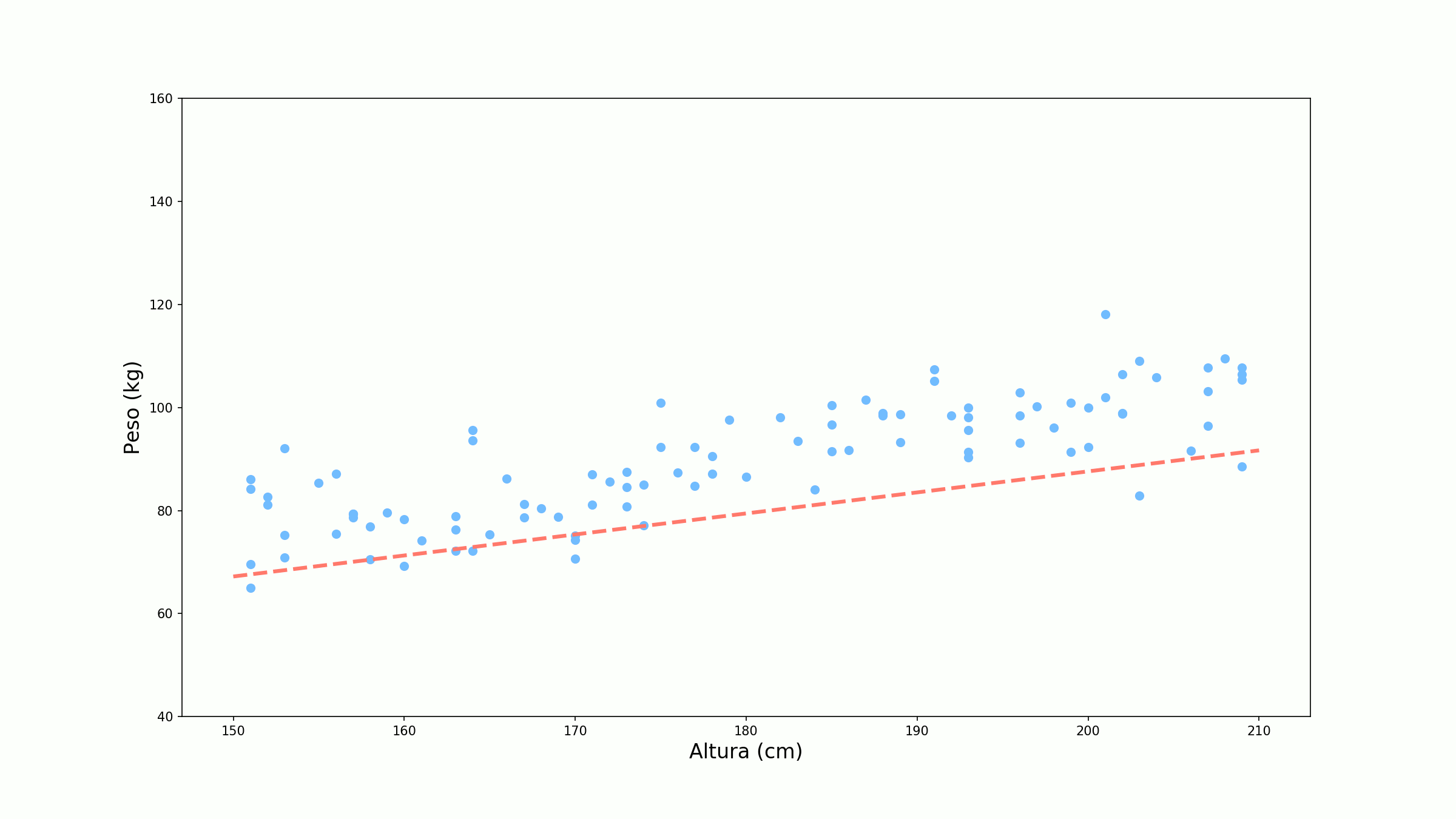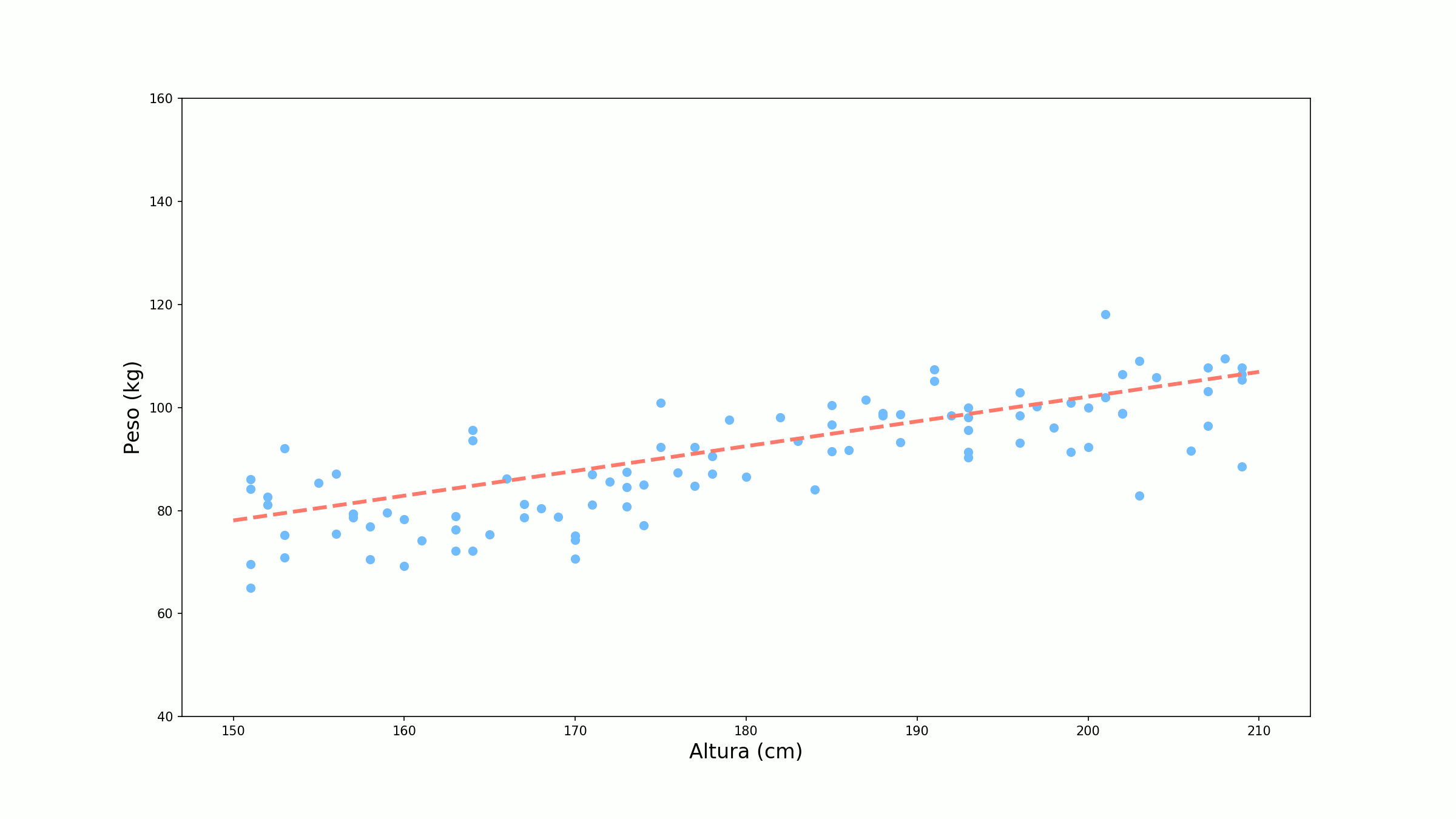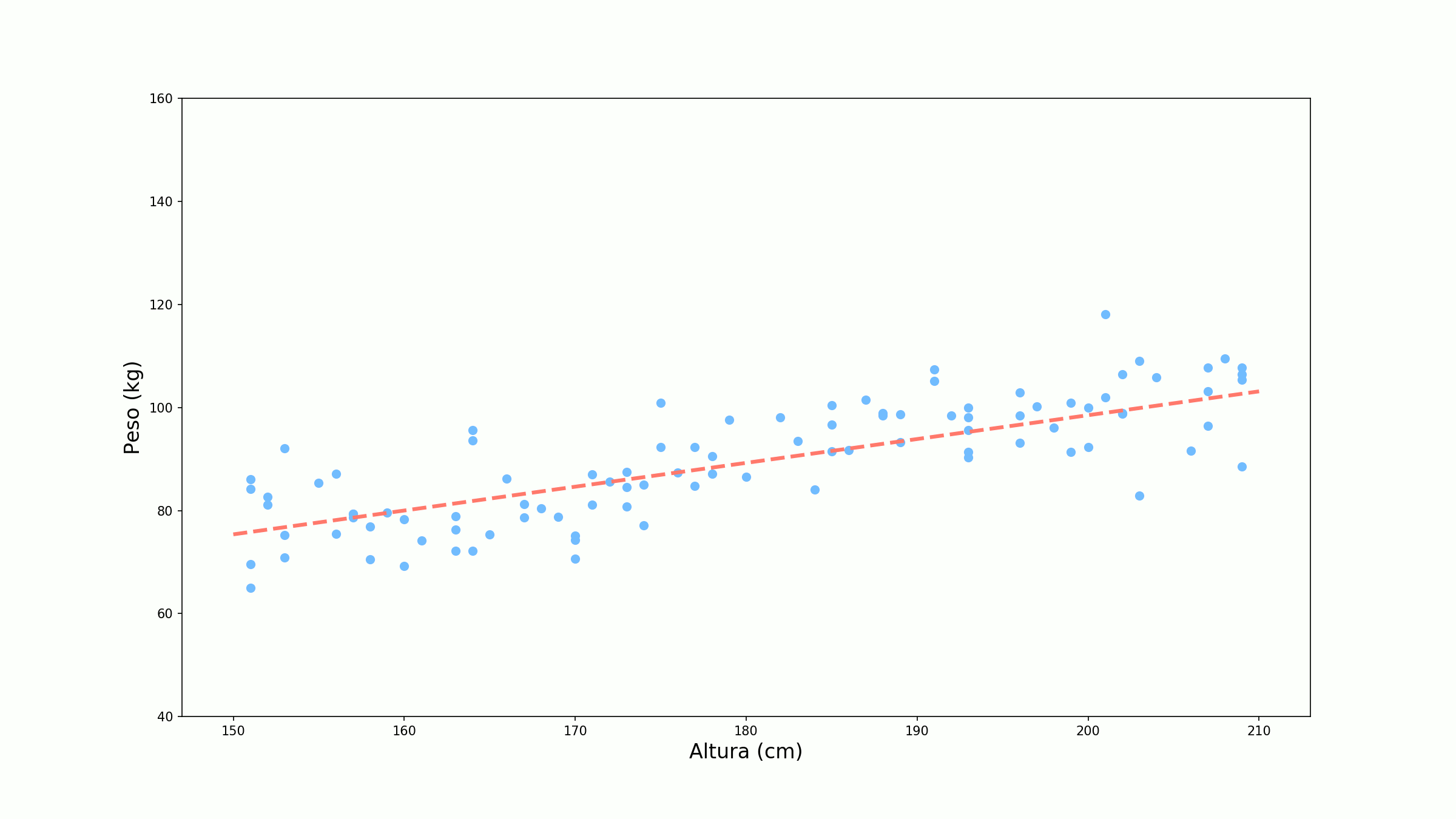
Backprogation
Nós discutimos até agora a rede com uma única camada. Mas como calculamos o gradiente quando temos camadas ocultas? Vamos tentar calculá-lo em uma rede bem simples (e que dificilmente será utilizada na prática).
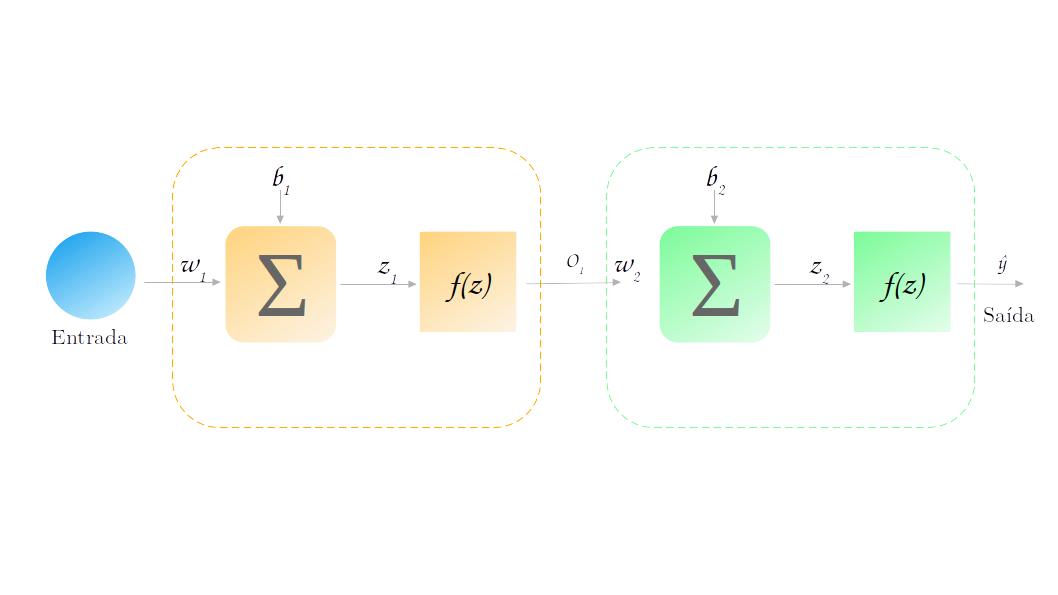
Vamos tentar calcular o gradiente de $\mathscr{L} (y, ŷ)$ (vamos usar a função de perda por simplicidade) em função do parâmetro $w_1$. Mas porque $w_1$ e não $w_2$? Lembre-se que já calculamos $w_2$ quando tratamos a regressão linear acima. Nosso intuito aqui é ver como propagamos o gradiente para a camada oculta.
Vamos então escrever as equações que levam a entrada na saída:
- $z_1 = w_1*x + b_1$
- $o_1 = f(z_1)$
- $z_2 = w_2*o_1 + b_2$
- $ŷ = f(z_2)$
Da mesma forma que fizemos anteriormente, vamos calculando as derivadas parciais utilizando a regra da cadeia:
-
$\frac{\partial \mathscr{L}}{\partial w_1} = \frac{\partial \mathscr{L}}{\partial ŷ} \frac{\partial ŷ}{\partial w_1} = (ŷ-y)\frac{\partial ŷ}{\partial w_1}$
-
$\frac{\partial ŷ}{\partial w_1} = \frac{\partial ŷ}{\partial z_2} \frac{\partial z_2}{\partial w_1} = f^\prime(z_2) \frac{\partial z_2}{\partial w_1}$
Até aqui tinhamos já havíamos feito. Vamos agora analisar $z_2$: o termo de $z_2$ que depende de $w_1$ é somente $o_1$. Dessa forma:
-
$\frac{\partial z_2}{\partial w_1} = \frac{\partial z_2}{\partial o_1} \frac{\partial o_1}{\partial w_1} = w_2 \frac{\partial o_1}{\partial w_1}$
-
$\frac{\partial o_1}{\partial w_1} = \frac{\partial o_1}{\partial z_1} \frac{\partial z_1}{\partial w_1} = f^\prime(z_1) \frac{\partial o_1}{\partial w_1}$
-
$\frac{\partial z_1}{\partial w_1} = x$
Combinando todas as equações:
\[\frac{\partial \mathscr{L}}{\partial w_1} = (ŷ-y) f^\prime(z_2) w_2 f^\prime(z_1) x\]Conseguimos! Obtivemos uma expressão para atualizar $w_1$ mesmo ele estando muito longe da saída. Observe que para fazermos isso, seguimos o sentido contrário da previsão: começamos da saída e chegamos até a entrada. Devido a esse comportamento, de propagação dos gradientes no sentido contrário à previsão, esse algoritmo é conhecido como backpropagation.
E agora?
Apesar de sabermos agora como as redes aprendem ainda existem questões a serem resolvidas como, por exemplo, por que utilizar a função de custo em vez da função de perda deixa o algoritmo mais estável. Esse será o tema do próximo artigo da série: Tipos de Gradiente Descendente. Não perca!